Skip to main content
LibreTexts - Ukrayinska

4.43:30-60-90 Прямі трикутники

  1. Last updated
  2. Save as PDF
  • Page ID
    54727

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Гіпотенуза дорівнює вдвічі найменшому катету, тоді як більший катет - в\(\sqrt{3}\) рази найменший.

    Один з двох спеціальних прямих трикутників називається трикутником 30-60-90, після його трьох кутів.

    30-60-90 Теорема: Якщо трикутник має кутові заходи\(30^{\circ}\)\(90^{\circ}\),\(60^{\circ}\) і, то сторони знаходяться в співвідношенні\(x:x\sqrt{3}:2x\).

    Чим коротший катет завжди х, тим довший катет завжди\(x\sqrt{3}\), а гіпотенуза завжди\(2x\). Якщо ви коли-небудь забудете ці теореми, ви все одно можете використовувати теорему Піфагора.

    Що робити, якщо вам дали 30-60-90 прямокутний трикутник і довжину однієї з його сторін? Як ви могли з'ясувати довжини його інших сторін?

    Приклад\(\PageIndex{1}\)

    Знайдіть значення\(x\) і\(y\).

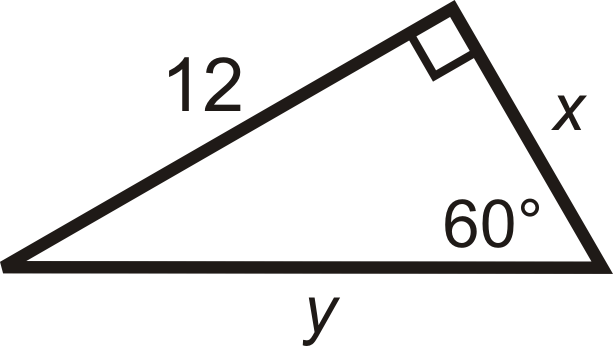
    F-д_Ф253Е0915А3А06ЕК 0d626 БД626 БДФ 759БДФ 5480908AD2FCD50348+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Рішення

    Нам дається довша нога.

    \(\begin{aligned} &x\sqrt{3} =12 \\ &x=\dfrac{12}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{12\sqrt{3}}{3}=4\sqrt{3} \\ &\text{The hypotenuse is} \\ &y=2(4\sqrt{3})=8\sqrt{3}\end{aligned}\)

    Приклад\(\PageIndex{2}\)

    Знайдіть значення\(x\) і\(y\).

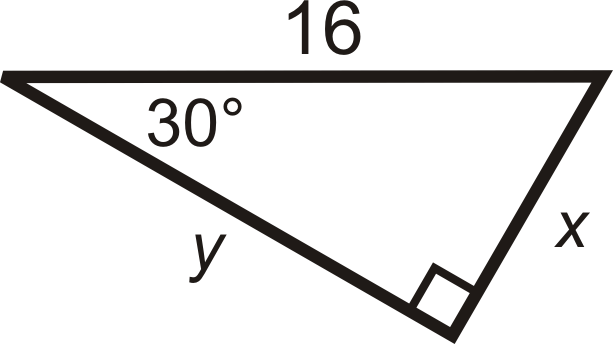
    F-д_54966Ф54 ААЕЦ 43БФД1Б94А46д9Б523714Д601Е30028766637C91A37+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Нам дано гіпотенузу.

    \(\begin{aligned}&2x=16 \\ &x=8 \\ &\text{The longer leg is} \\ &y=8\cdot \sqrt{3}=8\sqrt{3}\end{aligned}\)

    Приклад\(\PageIndex{3}\)

    Знайдіть довжину відсутніх сторін.

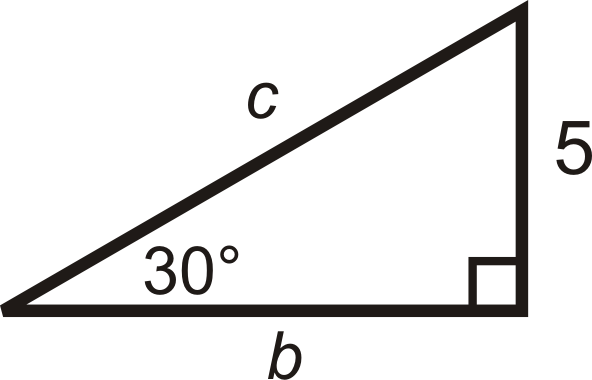
    F-D_6CF56285AC6D4E253C51867D19C5F1CF4D5EB5CCD2C207BC43F65D+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Нам дається коротша нога. Якщо\(x=5\), то довший катет\(b=5\sqrt{3}\), і гіпотенуза,\(c=2(5)=10\).

    Приклад\(\PageIndex{4}\)

    Знайдіть довжину відсутніх сторін.

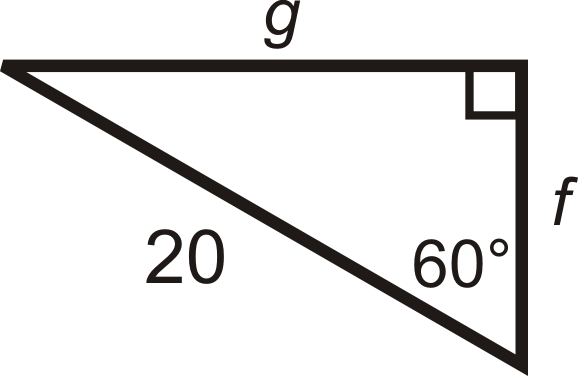
    F-D_382c5686A01A4042d0d0dc31E15FA8ФА9Ф0185Ф564Б927КД65Б93DC128+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Нам дано гіпотенузу. \(2x=20\), Таким чином, чим коротше нога\(f=\dfrac{20}{2}=10\), і довша нога,\(g=10\sqrt{3}\).

    Приклад\(\PageIndex{5}\)

    Прямокутник має сторони 4 і\(4\sqrt{3}\). Яка довжина діагоналі?

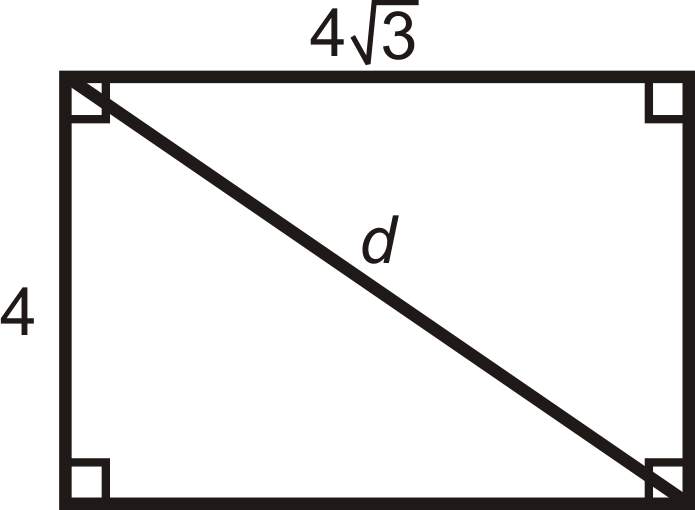
    Ф-д_БФБА 1 ФА Е7 БК БДФ Ф Ф 19д9ед 2213028 ДСБ883213 БК 48Ф78ЕА211АБ7+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Дві довжини\(x\)\(x\sqrt{3}\), так що діагональ буде\(2x\), або\(2(4)=8\).

    Якщо ви не визнали, що це трикутник 30-60-90, ви також можете використовувати теорему Піфагора.

    \(\begin{aligned} 4^2+(4\sqrt{3})^2&=d^2 \\ 16+48&=d^2 \\ d&=\sqrt{64}=8\end{aligned}\)

    Рецензія

    1. У трикутнику 30-60-90, якщо коротший катет дорівнює 5, то довший катет - __________, а гіпотенуза - ___________.
    2. У трикутнику 30-60-90, якщо коротший катет дорівнює х, то довший катет - __________, а гіпотенуза - ___________.
    3. Прямокутник має сторони довжиною 6 і\(6\sqrt{3}\). Яка довжина діагоналі?
    4. Дві (протилежні) сторони прямокутника - 10, а діагональ - 20. Яка довжина двох інших сторін?

    Для питань 5-12 знайдіть довжини відсутніх сторін. Спрощення всіх радикалів.

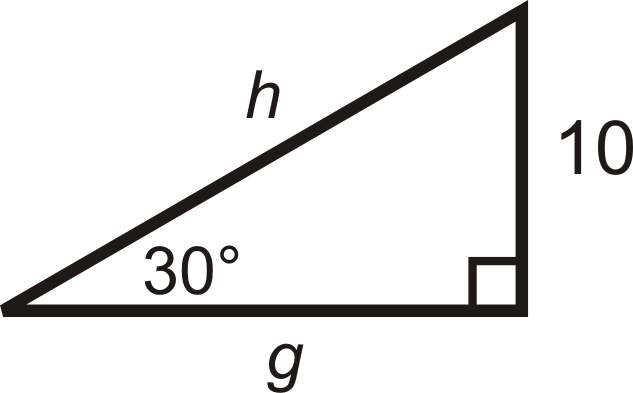
    1. F-D_2Facd 36BB2F Бусинка D849497ДД 107БА 534533Е6А88784CF8456C710384+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{6}\)
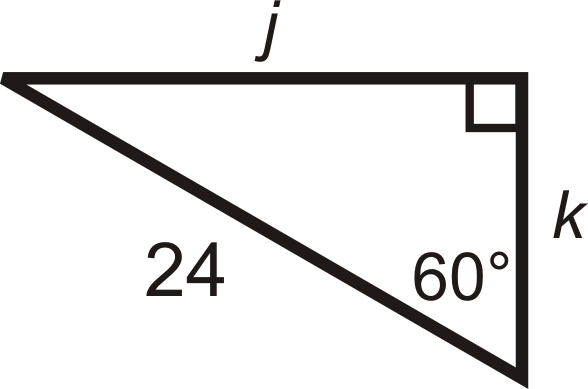
    2. F-д_Е677А66Е07Da6787e00079БД4С8Б21АБ821694093ФБФ ФБФ 62681E204E+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
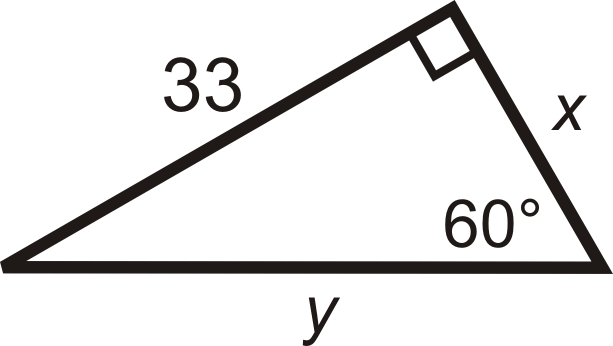
    3. Ф-д_1Ф29Ф072КБ73160Е 7892970886Б0С1Ф ЕБФ 8125Б24Б8БА 11683654АЕ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
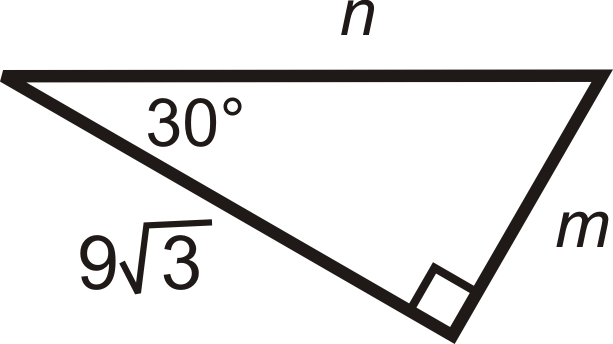
    4. F-D_C4D28ЕД 45 ДК897А6 ЕАД 6481Б0ДЕ495А862А1228Б6А361Ф6912Б49 ЕЕФ+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
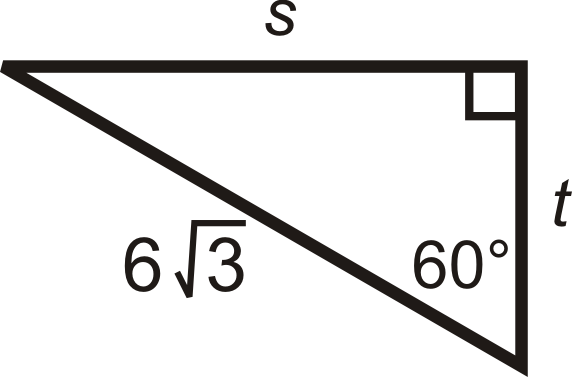
    5. Ф-д_39 дБ2Д0 ДД4С8617180356Ф22ДаФ 33Ф5009Д5Е91ЕФФ8К679ФД16КФБ+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
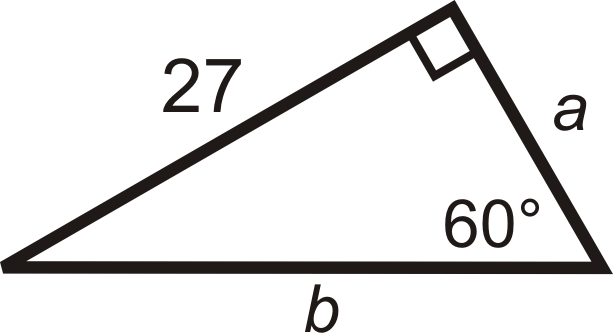
    6. Ф-Д_Е757021А70А51Б662А00Б9АФ 57195087812 ЕАД 33С7 ДБ373 CF0705D9+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
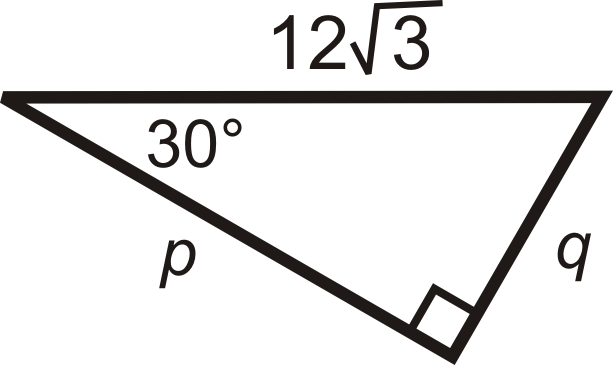
    7. F-д_9С3А73А 85Ф62650 Даф 5157Ф8 ЕЕ7 ДД59 ККС48А4А6631Ф25Д1728А0ФК+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
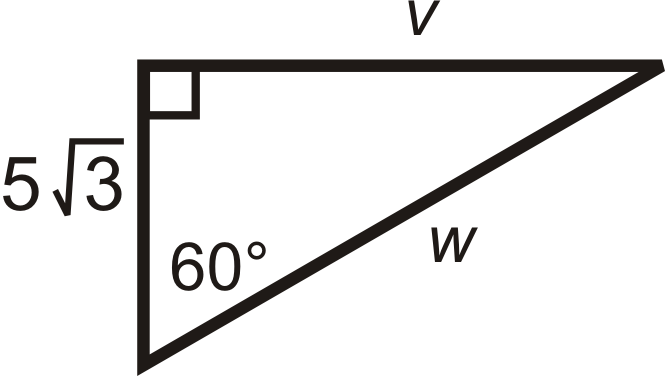
    8. F-д_6А 40679372417ФА67 ДБ43201А 11Е0А3Ф5КБ60ЕС698А15303644Д8570+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.6.

    Ресурси

    Лексика

    Термін Визначення
    Теорема 30-60-90 Якщо трикутник має кутові заходи 30, 60 і 90 градусів, то сторони знаходяться в співвідношенні\(x : x \sqrt{3} : 2x\)
    30-60-90 Трикутник Трикутник 30-60-90 - це спеціальний прямокутний трикутник з кутами\(30^{\circ}\)\(60^{\circ}\), і\(90^{\circ}\).
    Гіпотенуза Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута.
    Ніжки прямокутного трикутника Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута.
    Теорема Піфагора Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника, а c - гіпотенуза трикутника.
    Радикальний Знак\(\sqrt\), або квадратний корінь.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Розв'язування спеціальних правильних трикутників

    Види діяльності: 30-60-90 Прямі трикутники Обговорення Питання

    Навчальні посібники: Спеціальні правильні трикутники навчальний посібник

    Практика: 30-60-90 Прямі трикутники

    Реальний світ: боротьба з війною з наркотиками за допомогою геометрії та спеціальних трикутників