4.34: Розв'язування рівнянь з використанням теореми Піфагора
- Page ID
- 54912
Використовуйте a-квадрат+b-квадрат = c-квадрат, щоб знайти відсутні довжини сторін прямих трикутників.

Гарі хоче побудувати скейтборд рампи, але це не може бути занадто крутим. Якщо у нього майданчик висотою 3 м і дошка довжиною 5 м, як далеко повинна відходити дошка від платформи?
У цій концепції ви дізнаєтеся, як вирішувати рівняння за допомогою теореми Піфагора.
Теорема Піфагора стверджує, що сума квадратів двох катетів прямокутного трикутника дорівнює квадрату гіпотенузи. У математичному реченні, де a і b - катети, а c - гіпотенуза, це виглядає так:
\(c^2=a^2+b^2\)
Математично ви можете використовувати це рівняння для вирішення будь-якої зі змінних, а не тільки для гіпотенузи.
Наприклад, прямокутний трикутник внизу має один катет рівний 3 і гіпотенузу 5.
Вирішіть для іншої ноги.
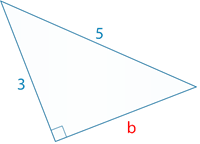
По-перше, ви можете позначити або ніжку,\(a\) або\(b\). Пам'ятайте, що ноги - це ті сторони, що прилягають до прямого кута.
Далі заповніть теорему Піфагора ті значення, які ви знаєте.
\(\begin{align*} c^2 &= a^2+b^2 \\ 5^2 &= 3^2+b^2 \end{align*}\)
Потім виконайте розрахунки, які ви в змозі.
\(25=9+b^2\)
Пам'ятайте, що ваша мета - ізолювати невідому змінну на одній стороні рівняння. В даному випадку це b і він кріпиться до квадрата і а+9. Виконайте необхідні операції по ізоляції б.
\(\begin{align*} 25−9 &= 9+b^2−9 \\ 16 &= b^2 \\ 4 &= b \end{align*}\)
Відповідь 4.
Приклад\(\PageIndex{1}\)
Раніше вам дали проблему з приводу Гері та його пандуса для скейт-дошки.
Рішення
Одна сторона, основа, була 4 м, а дошка, гіпотенуза, - 5 м. якою висотою буде пандус?

По-перше, підставляємо.
\(5^2=3^2+b^2\)
Далі виконуємо розрахунки.
\(\begin{align*} 25 &= 9+b^2 \\ 25−9 &= 9+b^2−9 \end{align*}\)
Потім визначте квадратні коріння.
\(\begin{align*} 16 &= b^2 \\ 4 &= b \end{align*}\)
Відповідь - 4 м. дошка Гері повинна простягатися на 4 м від основи платформи.
Приклад\(\PageIndex{2}\)
Вирішіть для b до найближчої десятої.
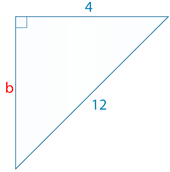
Рішення
Спочатку візьміть задані довжини і підставляйте їх у формулу.
\(\begin{align*} 4^2+b^2 &= 122 \\ 16+b^2 &= 144 \end{align*}\)
Далі віднімаємо 16 з обох сторін рівняння.
\(\begin{align*} 16−16+b^2 &= 144−16 \\ b^2 &= 128 \end{align*}\)
Потім візьміть квадратний корінь обох сторін рівняння.
\(b = 11.3137085 \ldots \)
Круглі на десяте місце
\(b\neq 11.3\)
Відповідь - 11,3
Приклад\(\PageIndex{3}\)
Прямокутний трикутник включає розміри\(a\),\(b=6\) і\(c=13\). Вирішити для\).
Рішення
По-перше, підставляємо.
\(\begin{align*} c^2 &= a^2+b^2 \\ 13^2 &= a^2+6^2 \end{align*}\)
Далі виконайте розрахунки, які ви в змозі.
\(\begin{align*} 169 &= a^2+36 \\ 169−36 &= a^2+36−36 \\ 133 &= a^2 \\ 11.532582594 \ldots &= a \\ 11.5 &\approx a \end{align*}\)
Відповідь є\(a=11.5\).
Приклад\(\PageIndex{4}\)
Прямокутний трикутник з\(a=8\)\(b\), і\(c=12\)
Рішення
По-перше, підставляємо.
\(\begin{align*} c^2 &= a^2+b^2 \\ 12^2 &= 8^2+b^2 \end{align*}\)
Далі виконуємо розрахунки.
\(\begin{align*} 144 &= 64+b^2 \\ 144−64 &= 64+b^2−64 \end{align*}\)
Потім визначте квадратні коріння.
\(\begin{align*} 80 &= b^2 \\ 8.9 &\neq b \end{align*}\)
Відповідь 8,9
Приклад\(\PageIndex{5}\)
Прямокутний трикутник з\(a=6\)\(b\), і\(c=10\)
Рішення
По-перше, підставляємо.
\(\begin{align*} c^2 &= a^2+b^2 \\ 10^2 &= 6^2+b^2 \end{align*}\)
Далі виконуємо розрахунки.
\(\begin{align*} 100 &= 36+b^2 \\ 100−36 &= 36+b^2−36 \end{align*}\)
Потім визначте квадратні коріння.
\(\begin{align*} 64 &= b^2 \\ 8 &= b \end{align*} \)
Відповідь - 8.
Рецензія
Використовуйте теорему Піфагора, щоб знайти довжину кожної відсутньої ноги. Ви можете округлити до найближчої десятої, коли це необхідно.
- \(a=6, \:b=?, \:c=12 \)
- \(a=9, \:b=?, \:c=15 \)
- \(a=4, \:b=?, \:c=5 \)
- \(a=9, \:b=?, \:c=18 \)
- \(a=15, \:b=?, \:c=25 \)
- \(a=?, \:b=10, \:c=12 \)
- \(a=?, \:b=11,\: c=14 \)
- \(a=?,\: b=13,\: c=15 \)
Напишіть рівняння за допомогою теореми Піфагора і розв'яжіть кожну задачу.
Джоанна поклала дошку з дерева вниз, щоб зробити пандус, щоб вона могла котити тачку по низькій стіні в своєму саду. Стіна заввишки 1,5 метра, а дошка з дерева торкається землі в 2 метрах від стіни. Скільки коштує дерев'яна дошка?
- Напишіть рівняння.
- Вирішіть за відповідь.
Кріс їхав на своєму велосипеді в 4 милі на захід, а потім 3 милі на південь. На якій найкоротшій відстані він може проїхати назад до того місця, де він почав?
- Напишіть рівняння.
- Вирішити проблему.
Наомі вирізає трикутні латки, щоб зробити ковдру. Кожен має діагональну сторону 14,5 дюймів і коротку сторону 5,5 дюймів. Яка довжина третьої сторони кожного трикутного латки?
- Напишіть рівняння.
- Вирішити проблему.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Гіпотенуза | Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута. |
| Ніжки прямокутного трикутника | Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута. |
| Теорема Піфагора | Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника, а c - гіпотенуза трикутника. |
Додаткові ресурси
Інтерактивний елемент
Відео: Теорема Піфагора зі змінними: зразок застосування
Практика: Розв'язування рівнянь з використанням теореми Піфагора
Реальний світ: загадкові нотатки