4.35: Додатки, що використовують теорему Піфагора

Задачі слів з використанням теореми Піфагора.

Теорема Піфагора та її зворотна мають багато застосувань для пошуку довжин та відстаней.

Застосування в реальному світі: Діагональна довжина

Марія має прямокутний лист печива, який вимірює\(10\: inches\times 14\: inches\). Знайдіть довжину діагоналі листа печива.

Намалюйте ескіз:

Малюнок\(\PageIndex{1}\)

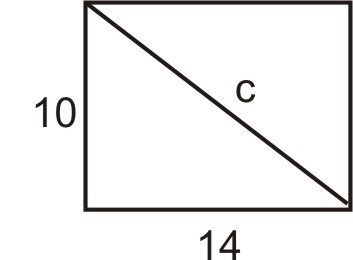
Визначити змінні: Нехай\(c= length\: of \:the\: diagonal\).

Напишіть формулу: Використовуйте теорему Піфагора:\(a^2+b^2=c^2\)

Розв'яжіть рівняння:

\(\begin{align*}10^2+14^2=c^2 \\ 100+196=c^2 \\ c^2=296\Rightarrow c=\sqrt{296}\Rightarrow c=2\sqrt{74} \:or\: c=17.2\: inches\end{align*}\)

Перевірка:\(10^2+14^2=100+196=296\) і\(c^2=17.2^2=296\). Рішення перевіряє.

Застосування в реальному світі: Площа затінених областей

Знайдіть площу затіненої області на наступній схемі:

Малюнок\(\PageIndex{2}\)

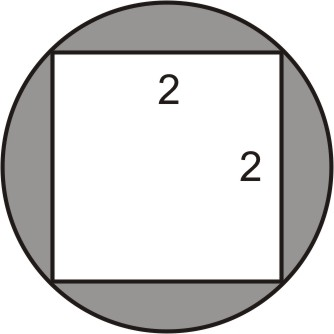
Намалюйте діагональ квадрата на малюнку:

Малюнок\(\PageIndex{3}\)

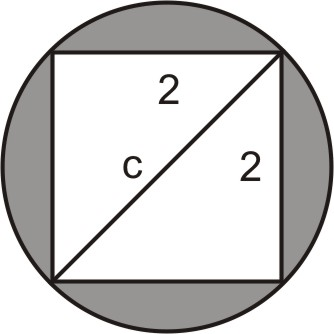
Зверніть увагу, що діагональ квадрата - це також діаметр кола.

Визначити змінні: Нехай\(c= diameter\: of\: the\: circle\).

Напишіть формулу: Використовуйте теорему Піфагора:\(a^2+b^2=c^2\).

Розв'яжіть рівняння:

\(\begin{align*}2^2+2^2=c^2 \\ 4+4=c^2 \\ c^2=8\Rightarrow c=\sqrt{8}\Rightarrow c=2\sqrt{2}\end{align*}\)

Діаметр окружності дорівнює\(2\sqrt{2}\), отже, радіус\(R=\sqrt{2}\).

Формула площі кола:\(A=\pi\cdot R^2=\pi(\sqrt{2})^2=2\pi\).

Таким чином, площа затіненої області є\(2\pi−4=2.28\).

Застосування в реальному світі: вимірювання сторін трикутника

У прямокутному трикутнику одна ніжка в два рази довша за іншу, а периметр - 28. Які міри сторін трикутника?

Зробіть ескіз і визначте змінні:

Малюнок\(\PageIndex{4}\)

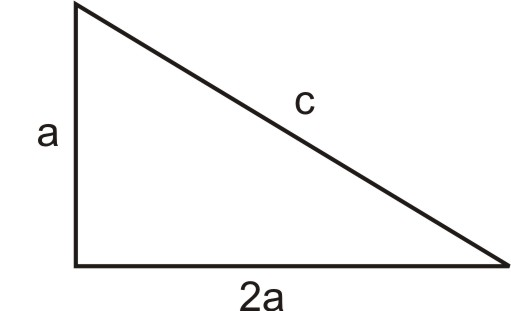
Нехай:\(a= length\: of \:the \:short \:leg\)

\(2a= length \:of \:the \:long \:leg\)

\(c= length \:of \:the \:hypotenuse\)

Напишіть формули:

Сторони трикутника пов'язані двома різними способами.

Периметр дорівнює 28, так\(a+2a+c=28\Rightarrow 3a+c=28\)

Трикутник - прямокутний трикутник, тому міри сторін повинні задовольняти теоремі Піфагора:

\(\begin{align*}&&&a^2+(2a)^2=c^2\Rightarrow a^2+4a^2=c^2\Rightarrow 5a^2=c^2 \\ &or& \qquad &c=a\sqrt{5}=2.236a\end{align*}\)

Розв'яжіть рівняння:

Підключіть щойно отримане нами значення c в рівняння периметра:\(3a+c=28\)

\(3a+2.236a=28\Rightarrow 5.236a=28\Rightarrow a=5.35\)

Коротка нога - це:\(a=5.35\)

Довга нога - це:\(2a=10.70\)

Гіпотенуза буває:\(c=11.95\)

Перевірка: Ніжки трикутника повинні задовольняти теоремі Піфагора:

\(a^2+b^2=5.35^2+10.70^2=143.1\),\(c^2=11.95^2=142.80\). Результати приблизно однакові.

Периметр трикутника повинен бути 28:

\(a+b+c=5.35+10.70+11.95=28\). Відповідь перевіряється.

Приклад\(\PageIndex{1}\)

Майк завантажує рухомий фургон, піднімаючись по рампі. Пандус має довжину 10 футів, а ліжко фургона - 2,5 футів над землею. Як далеко пандус простягається повз задньої частини фургона?

Рішення

Робимо ескіз:

Малюнок\(\PageIndex{5}\)

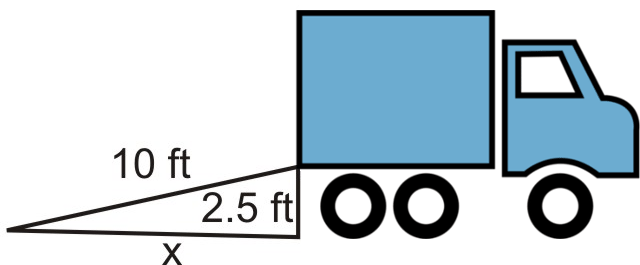
Визначити змінні: Нехай\(x= how\: far \:the \:ramp \:extends \:past \:the \:back \:of \:the \:van\).

Напишіть формулу: Використовуйте теорему Піфагора:\(x^2+2.5^2=10^2\)

Розв'яжіть рівняння:

\(\begin{align*} x^2+6.25=100 \\ x^2=93.5 \\ x=\sqrt{93.5}=9.7 ft\end{align*} \)

Перевірте, підключивши результат до теореми Піфагора:

\(9.7^2+2.5^2=94.09+6.25=100.34\neq 100\). Таким чином, пандус має довжину 10 футів. Відповідь перевіряється.

Рецензія

1. Для того щоб зробити пандус, який\(3\:ft high and covers \(4\:ft\) із землі, скільки повинен бути пандус?
2. Регулювання бейсбол алмаз є квадрат з 90 футів між базами. Як далеко друга основа від домашньої плити?
3. У Емануеля є картонна коробка, яка вимірює\(20\: cm \:long \times 10 \:cm \:wide \times 8 \:cm \:deep\).
   1. Яка довжина діагоналі поперек дна коробки?
   2. Яка довжина діагоналі від нижнього кута до протилежного верхнього кута?
4. Самуїл ставить сходи проти свого будинку. Підстава сходів знаходиться в 6 футах від будинку, а сходи довжиною 10 футів.
   1. Наскільки високо над землею сходи торкаються стіни будинку?
   2. Якщо край даху знаходиться на відстані 10 футів від землі і стирчить 1,5 футів за стіну, як далеко він знаходиться від краю даху до верхньої частини сходів?
5. Знайдіть площу трикутника нижче, якщо площа трикутника визначена як A=12 base\ times висота:

   

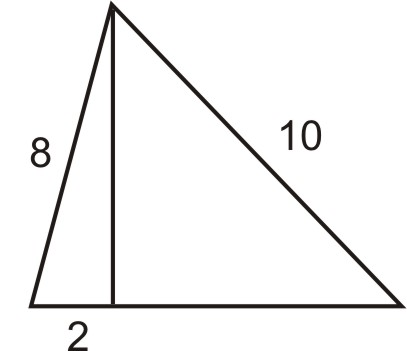
   Малюнок\(\PageIndex{6}\)

6. Замість того, щоб ходити по двох сторонам прямокутного поля, Маріо вирішив перерізати поперек діагоналі. Він таким чином економить відстань, яка становить половину довгої сторони поля.
   1. Знайдіть довжину довгої сторони поля, враховуючи, що коротка сторона становить 123 фути.
   2. Знайдіть довжину діагоналі.
7. Маркус пливе на північ, а Сандра відпливає на схід від тієї ж відправної точки. За дві години човен Маркуса знаходиться в 35 милі від початкової точки, а човен Сандри - в 28 милі від початкової точки.
   1. Як далеко човни один від одного?
   2. Сандра потім пливе 21 милю через північ, поки Маркус залишається на місці. Як далеко Сандра від початкової відправної точки?
   3. Як далеко Сандра від Маркуса?
8. Визначте площу кола нижче. (Підказка: гіпотенуза трикутника - це діаметр кола.)

   

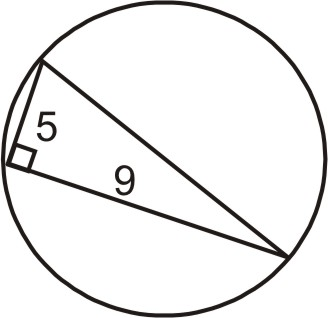
   Малюнок\(\PageIndex{7}\)

9. Довжина прямокутника\(1\:in\) довша за його ширину, а діагональ має довжину\(29\:in\). Які довжини сторін прямокутника?
10. Для рівнобедреного трикутника зі сторонами заданої довжини знайдіть довжину кожної гіпотенузи:
    1. 1
    2. 2
    3. 3
    4. \(n\)

Лексика

Термін	Визначення
зворотний	Якщо умовний оператор є\(p\rightarrow q\) (\(p\)if, то\(q\)), то зворотним є\(q\rightarrow p\) (if\(q\), то\(p\)). Зауважте, що зворотне твердження не відповідає дійсності лише тому, що оригінальне твердження є істинним.

Додаткові ресурси

Відео: Рішення проблем слів за участю квадратних коренів - огляд

Практика: Додатки з використанням теореми Піфагора