Skip to main content
LibreTexts - Ukrayinska

4.33: Теорема Піфагора та її зворотне

  1. Last updated
  2. Save as PDF
  • Page ID
    54761

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використовуйте a-квадрат+b-квадрат = c-квадрат, щоб довести, що трикутники є прямими трикутниками.

    Припустимо, ви качаєте намет, а 8-футовий стовп робить прямий кут із землею. Якщо мотузка йде від верхньої частини стовпа до точки на землі 12 футів від основи стовпа, як довго мотузка? Як би ви розрахували його довжину?

    Теорема Піфагора та її зворотне

    Теорема Піфагора

    Однією з найважливіших теорем в математиці і науці є теорема Піфагора. Простіше кажучи, він стверджує: «Сума квадрата кожного катета прямокутного трикутника дорівнює квадрату гіпотенузи».

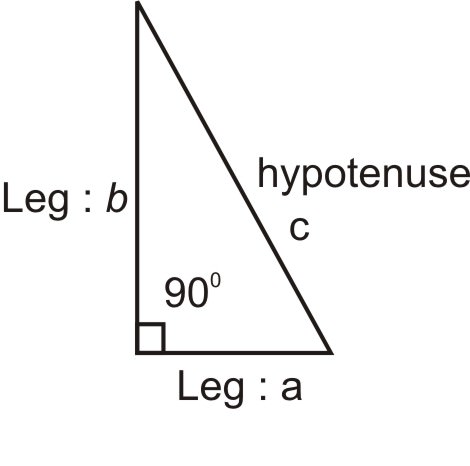
    Ф-Д_371289А4БФ Ф8Б32ДЕ172 ЕСФ 321 ФД 649Б4899930CBE62Б5Е0Ф73ЕД50+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{1}\)

    Прямокутний трикутник - це трикутник з прямим кутом. Розглянемо основні анатомії прямокутного трикутника.

    Два відрізки, що утворюють прямий кут (\(90^{\circ}\)), називаються ніжками прямокутного трикутника. Відрізок, протилежний прямому куту, називається гіпотенузою.

    Теорема Піфагора говорить\((leg_1)^2+(leg_2)^2=(hypotenuse)^2\):

    \(a^2+b^2=c^2\)

    Або, щоб знайти гіпотенузу,\(c=\sqrt{a^2+b^2}\).

    Зверніть увагу, що це співвідношення вірно лише для правильних трикутників. На більш пізніх курсах ви навчитеся визначати відносини з непрямими трикутниками.

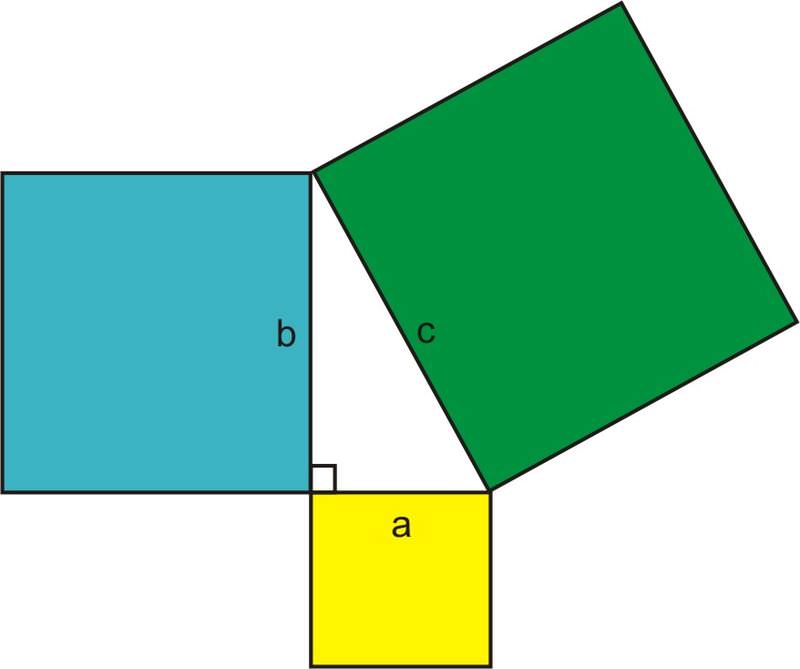
    Хоча ми зазвичай посилаємося на теорему Піфагора при визначенні довжин сторін прямокутного трикутника, теорема спочатку зробила твердження про області. Якщо будувати квадрати з кожного боку прямокутного трикутника, то теорема Піфагора говорить, що площа квадрата, стороною якого є гіпотенуза, дорівнює сумі площ квадратів, утворених катетами трикутника.

    Ф-д_7ЕФ2381245ФБ7А925С9 СА3858Ф593А10Е5161С10ДА0827C6ЕЕЕЦ2Ф2А+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{2}\)

    Конверс теореми Піфагора

    Повернення теореми Піфагора також вірно. Тобто, якщо довжини трьох сторін трикутника роблять рівняння\(a^2+b^2=c^2\) істинним, то вони представляють сторони прямокутного трикутника.

    З цим зворотним, ви можете використовувати теорему Піфагора, щоб довести, що трикутник - це прямокутний трикутник, навіть якщо ви не знаєте жодного з вимірювань кута трикутника.

    Давайте завершимо наступні завдання, що стосуються прямокутних трикутників і теореми Піфагора:

    1. Чи містить трикутник нижче прямий кут?
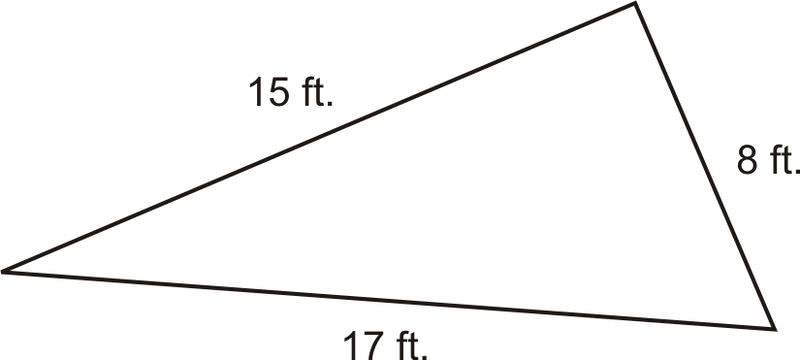
    Ф-Д_455127А6А97Д017С04Ф 56163Д8Е5АФ 72220231Ф8822ФА82412+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{3}\)

    Цей трикутник не має жодних прямокутних знаків або виміряних кутів, тому ви не можете припустити, що ви знаєте, чи є трикутник гострим, правильним чи тупим, просто дивлячись на нього. Знайдіть хвилинку, щоб проаналізувати довжину сторін і подивитися, як вони пов'язані. Дві сторони, 15 і 17, відносно близькі по довжині. Третя сторона, 8, становить приблизно половину довжини двох довших сторін.

    Щоб побачити, чи може трикутник бути правильним, спробуйте замінити довжини сторін у теорему Піфагора, щоб перевірити, чи роблять вони рівняння істинним. Гіпотенуза завжди найдовша сторона, тому 17 слід підставити на c Два інших значення можуть представляти a і b і порядок не важливий.

    \(\begin{align*} a^2+b^2&=c^2 \\ 8^2+15^2&=17^2 \\ 64+225&=289 \\ 289&=289\end{align*}\)

    Оскільки обидві сторони рівняння рівні, ці значення задовольняють теоремі Піфагора. Тому описаний в задачі трикутник є прямокутним трикутником.

    1. Одна ніжка прямокутного трикутника на 5 більше, ніж інша ніжка. Гіпотенуза більше ніж в два рази перевищує розмір короткого катета. Знайдіть розміри трикутника.

    Нехай x = довжина короткої ноги. Потім,\(x+5= length\:of \:the \:long \:leg\) і\(2x+1= length \:of \:the \:hypotenuse\).

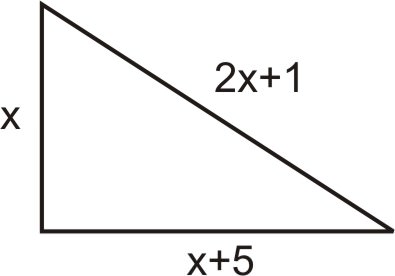
    Ф-Д_9Е407Ф1874906265628857 ЕС54С66Б4С4Д8302А29Ф672Ф38Б3КС8E+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{4}\)

    Сторони трикутника повинні задовольняти теоремі Піфагора.

    \(\begin{align*} & & x^2+(x+5)^2 &=(2x+1) \\ &Eliminate \:the \:parentheses. &\qquad x^2+x^2+10x+25 &=4x^2+4x+1 \\ &Move \:all \:terms \:to \:the \:right \:hand \:side \:of \:the \:equation. &\qquad 0 &=2x^2−6x−24 \\ &Divide \:all \:terms \:by \:2. &\qquad 0 &=x^2−3x−12 \\ &Solve \:using \:the \:quadratic \:formula. &\qquad x &=\dfrac{3 \pm \sqrt{9+48}}{2}=\dfrac{3 \pm \sqrt{57}}{2} \\ & & x &\neq 5.27 \:or \:x\neq −2.27 \end{align*}\)

    Негативне рішення не має сенсу в контексті даної проблеми. Отже, використовуємо\(x=5.27\) і отримуємо

    \(short\:−leg=5.27,\: long\:−leg=10.27\)і

    \(hypotenuse=11.54\).

    1. Знайдіть площу затіненої області на наступній схемі.
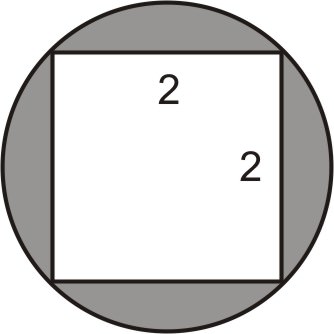
    Ф-Д_Е0А9 ААА 63Б0 АААА 55CB2027503С2ДФ 25640Ф862Б69 CF3287C9CF0CB8+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{5}\)

    Намалюйте діагональ квадрата на малюнку.

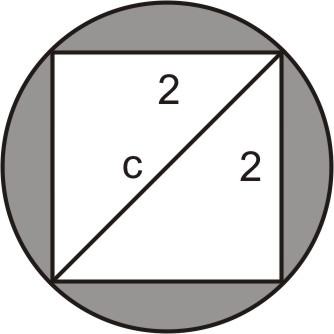
    Ф-Д_Д3Е 900Е645А675Е 188ФК 094 ФДКА1Д7ДБ Б 2Б3Ф892Е4Б56С9Б4Ф8Е1ЕД7+зображення_крихіткий+зображення_крихіткий.jpg
    Малюнок\(\PageIndex{6}\)

    Зверніть увагу, що діагональ квадрата - це також діаметр кола.

    Визначте змінні. Нехай\(c= diameter\: of\: the\: circle\).

    \(\begin{align*} & & 2^2+2^2 &= c^2 \\ & & 4+4 &=c^2 \\ &Write\: the \:formula \:and \:solve. \: & c^2 & = 8\Rightarrow c=\sqrt{8}\Rightarrow c=2\sqrt{2}\end{align*}\)

    Діаметр кола дорівнює\(2\sqrt{2}\). Тому радіус є\(r=\sqrt{2}\).

    Площа кола дорівнює\(A=\pi r^2=\pi (\sqrt{2} )^2=2\pi\).

    Отже, площа затіненої області дорівнює 2\ pi −4\ neq 2.28\).

    Приклад\(\PageIndex{1}\)

    Раніше вас попросили знайти довжину мотузки, яку ви використовували для розміщення намету. Ви знаєте, що мотузка йде від вершини 8 футовий полюс до точки на землі 12 футів від основи.

    Рішення

    Цю ситуацію можна уявити прямокутним трикутником.

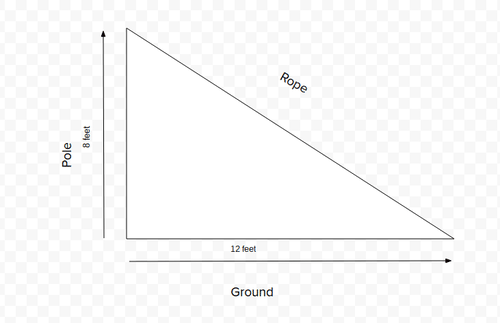
    F-D_721826059B027D0A296F1EDFCB729F1602C06CCC97995cda097b0206+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Припускаючи, що кут між землею і полюсом дорівнює 90 градусам, ми можемо використовувати теорему Піфагора для вирішення довжини мотузки.

    Нехай\(a= 8 \:feet (length of the pole), \(b= 12\:feet\) (відстань від жердини до мотузки на землі), і\(c= the\:length \:of \:the \:rope\).

    \(\begin{align*}a^2+b^2&=c^2 \\ 8^2+12^2&=c^2 \\ 208&=c^2 \\ c&=\sqrt{208} \\ c&=\sqrt{16}\sqrt{13} \\ c&=4\sqrt{13}\:feet \end{align*}\)

    Мотузка довжиною\(4\sqrt{13} \) ноги.

    Приклад\(\PageIndex{2}\)

    Визначте, чи утворює трикутник зі сторонами довжин 5, 6 і 8 прямокутний трикутник.

    Рішення

    Використовуйте Converse теореми Піфагора:

    \(\begin{align*} Start \:with \:the \:Pythagorean \:equation.&\qquad a^2+b^2 &=c^2 \\ Substitute \:in \:the \:values \:of \:the\: sides. &\qquad 5^2+6^2&\stackrel{?}{=}8^2 \\ Simplify. &\qquad 25+36 &\stackrel{?}{=}64 \\ Check. &\qquad 61 &\neq 64\end{align*} \)

    Оскільки ці довжини сторін не задовольняють рівнянню теореми Піфагора, трикутник не є прямокутним трикутником.

    Рецензія

    Переконайтеся, що кожен трикутник є прямокутним трикутником.

    1. \(a=12, \:b=9,\:c=15\)
    2. \(a=6, \:b=6, \:c=6\sqrt{2}\)
    3. \(a=8, \:b=8\sqrt{3}, \:c=16\)

    Знайдіть відсутню довжину кожного прямокутного трикутника.

    1. \(a=12,\: b=16, \:c=?\)
    2. \(a=?, \:b=20, \:c=30\)
    3. \(a=4, \:b=?, \:c=11\)
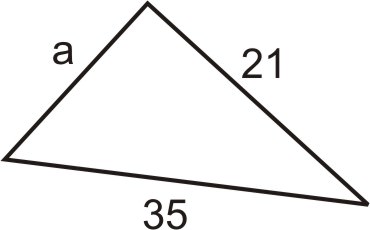
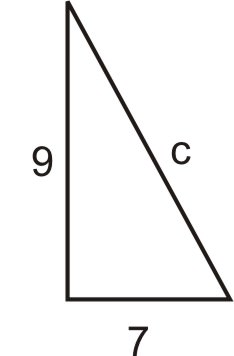
    4. Ф-Д_32632Е08С93КА45198Е Е 35384340А303899Е8Ф8Ф81А872480Е02ДК83А+зображення_крихіткий+зображення_крихіткий.jpg
      Малюнок\(\PageIndex{8}\)
    5. Ф-Д_5Б4 СБ 9888887 АА4С3Д494АФ 6ЕЕ267 ДД52253208ДД02798677ДБА51Б74+зображення_крихіткий+зображення_крихіткий.jpg
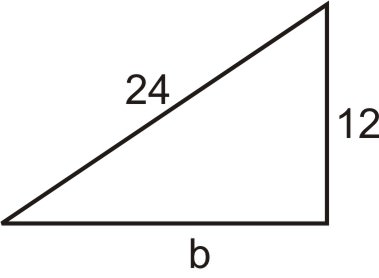
      Малюнок\(\PageIndex{9}\)
    6. Ф-Д_Е717Ф6855Б4Е48 ДС612ББА 615Е4А2965Д2А48КС0КА5019БФ387Б4А8+зображення_крихіткий+зображення_крихіткий.JPG
      Малюнок\(\PageIndex{10}\)
    7. Один катет прямокутного трикутника на 4 фути менше гіпотенузи. Інша нога - 12 футів. Знайдіть довжини трьох сторін трикутника.
    8. Одна ніжка прямокутного трикутника на 3 більше, ніж в два рази більше довжини іншого. Гіпотенуза в 3 рази перевищує довжину короткого катета. Знайдіть довжини трьох ніжок трикутника.
    9. Регулювання бейсбол алмаз є квадрат з 90 футів між базами. Як далеко друга основа від домашньої плити?
    10. У Емануеля є картонна коробка, яка вимірює\(20\: cm\times 10\: cm\times 8\: cm\) (\(length\times width\times height\)). Яка довжина діагоналі від нижнього кута до протилежного верхнього кута?
    11. Самуїл ставить сходи проти свого будинку. Підстава сходів знаходиться в 6 футах від будинку, а сходи довжиною 10 футів. Наскільки високо над землею сходи торкаються стіни будинку?
    12. Знайдіть площу трикутника, скориставшись формулою\(A=\dfrac{1}{2}base\times height\).
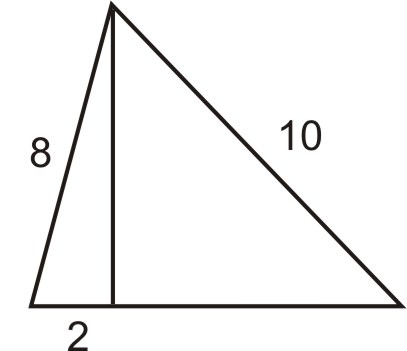
      Ф-Д_Б181 Е89651238Е10ААЕ 3177 СС95ДБ 92954 ФДК8Б1АЕ147Е1С289Е2+зображення_крихіткий+зображення_крихіткий.JPG
      Малюнок\(\PageIndex{11}\)
    13. Замість того, щоб ходити по двох сторонам прямокутного поля, Маріо вирішив перерізати поперек діагоналі. Він економить відстань, яка становить половину довгої сторони поля. Знайдіть довжину довгої сторони поля, враховуючи, що коротка сторона становить 123 фути.
    14. Маркус пливе на північ, а Сандра відпливає на схід від тієї ж відправної точки. За дві години човен Маркуса знаходиться в 35 милі від початкової точки, а човен Сандри - за 28 миль від початкової точки. Як далеко човни один від одного?
    15. Визначте площу кола.
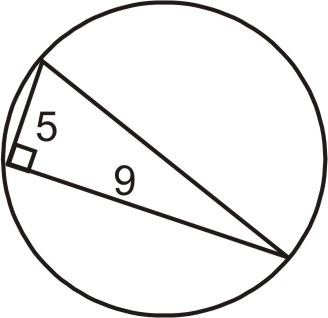
      Ф-Д_А78659629Д42Д58КА4Б19Е389С1А8914 ФК3С515А0С184218Е12Е37+зображення_крихіткий+зображення_крихіткий.jpg
      Малюнок\(\PageIndex{12}\)
    16. У прямокутному трикутнику одна ніжка в два рази довша за іншу, а периметр - 28. Які міри сторін трикутника?
    17. Марія має прямокутний лист печива, який вимірює\(10\:inches\times 14\:inches\). Знайдіть довжину діагоналі листа печива.
    18. Майк завантажує рухомий фургон, піднімаючись рампу. Пандус має довжину 10 футів, а ліжко фургона - 2,5 футів над землею. Як далеко пандус простягається повз задньої частини фургона?

    Швидка вікторина

    1. Визначте походження\(h(x)=\sqrt{x−2}+5\), а потім графік функції.
    2. Спростити\(6\sqrt[3]{2}\) шляхом раціоналізації знаменника.
    3. Спростити:\(\sqrt[4]{−32}\). Якщо відповідь неможлива, поясніть, чому.
    4. Що таке стороннє рішення? В яких ситуаціях виникають подібні рішення?
    5. Чи можуть сторони довжиною 3, 4 та 6 утворювати прямокутний трикутник?
    6. Вирішити\(5=y+\sqrt[3]{y+6}\).

    Лексика

    Термін Визначення
    зворотна теорема Піфагора Якщо довжини трьох сторін трикутника задовольняють рівнянню\(a^2+b^2=c^2\), то трикутник - прямокутний трикутник.
    зворотний Якщо умовний оператор є\(p\rightarrow q\) (\(p\)if, то\(q\)), то зворотним є\(q\rightarrow p\) (if\(q\), то\(p\). Зауважте, що зворотне твердження не відповідає дійсності лише тому, що оригінальне твердження є істинним.
    Гіпотенуза Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута.
    Ніжки прямокутного трикутника Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута.
    Теорема Піфагора Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника, а c - гіпотенуза трикутника.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Теорема Піфагора - огляд

    Види діяльності: Теорема Піфагора та її зворотні дискусійні питання

    Практика: теорема Піфагора та її зворотне

    Реальний світ: Карта SF - PythM