4.28: Основи теореми Піфагора
- Page ID
- 54798
Визначте трійки і обчислити відсутні сторони. Використовуйте програми непрямих вимірювань
Вивести і використовувати теорему Піфагора

Кошеня Трейсі застряг на 2,8 метрів над землею на підвіконні будинку її бабусі. Її бабуся не вдома, тому вона вирішує врятувати свого жахливого кошеня за допомогою своїх друзів. З міркувань безпеки основа сходів повинна знаходитися на відстані 0,7 м від будинку і простягатися на 1 двір над підвіконням. Сходи, яку вона запозичила, має довжину 4 ярди.
Коли Трейсі позиціонує сходи на місці, вона дивиться вгору і дивується, чи буде сходи достатньо високою, щоб вона врятувала свого кошеня.
У цьому понятті ви навчитеся виводити і використовувати теорему Піфагора.
Теорема Піфагора
Трикутники часто називаються відповідно до міри кутів, які вони містять. Гострий трикутник має три кути такі, що кожен з трьох кутів менше\(90^{\circ}\). Тупий трикутник має два кути такі, що міра кожного з цих кутів менше, ніж,\(90^{\circ}\) а міра третього кута більше\(90^{\circ}\). Прямокутний трикутник має один кут, який має міру\(90^{\circ}\) і два гострі кути таким чином, що сума їх мір дорівнює\(90^{\circ}\). Два гострі кути прямокутного трикутника є взаємодоповнюючими — їх сума дорівнює\(90^{\circ}\).
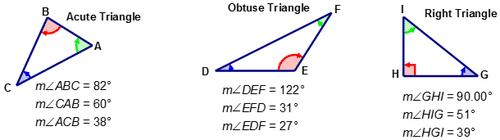
З трьох трикутників, показаних на наведеній вище схемі, прямокутний трикутник - це той, який використовується найчастіше при вирішенні реальних завдань. Цей тип трикутника має характеристики, унікальні лише для правильних трикутників. Кожен трикутник має три сторони і три кути. Сторони прямокутного трикутника мають назви, які застосовуються тільки до прямокутного трикутника.
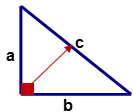
Дві сторони прямокутного трикутника з позначками 'a' і 'b' називаються ніжками трикутника. Сторона трикутника навпроти прямого кута (\(90^{\circ}\)), позначеного «c», називається гіпотенузою і є найдовшою стороною прямокутного трикутника. Імена катетів 'a' і 'b' можуть бути переключені з одного катета на інший, але гіпотенуза 'c' повинна бути стороною, протилежною прямому куту трикутника.
Зв'язок між гіпотенузою та катетами прямокутного трикутника визначається теоремою Піфагора, яка стверджує, що квадрат довжини гіпотенузи дорівнює сумі довжини катета 'a' в квадраті і довжини катета 'b' в квадраті. Теорема Піфагора викладена рівнянням.
\(c^2= a^2+b^2\)
Рівняння, що представляє теорему Піфагора, містить три частини, які є a, b і c Якщо ви знаєте дві з цих частин, то рівняння може бути використано для обчислення третього фрагмента. Теорема Піфагора також може бути використана для визначення того, чи дійсно даний трикутник є прямокутним трикутником.
Подивіться на трикутник, наведений нижче. Немає прямого кута, позначеного, щоб вказати, що трикутник є прямокутним трикутником. Трикутник - це прямокутний трикутник? Теорема Піфагора може бути використана для відповіді на це питання.
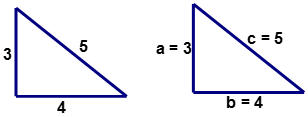
\(c^2=a^2+b^2\)
Спочатку заповніть значення для букв\(a\),\(b\) і\(c\).
\(\begin{align*}c^2&=a^2+b^2 \\ (5)^2&=(3)^2+(4)^2\end{align*}\)
Далі виконуємо зазначені операції по обидва боки рівняння.
\(\begin{align*}(5)^2&=(3)^2+(4)^2 \\ (5\times 5)&=(3\times 3)+(4\times 4) \\ 25&=9+16\end{align*}\)
Потім спростіть рівняння, додавши значення в правій частині рівняння.
\(\begin{align*}25&=9+16 \\ 25&=25\end{align*}\)
Обидві сторони рівняння рівні. Значення (3, 4 і 5) призвели до того, що\ (c^2=a^2+b^2 є істинним твердженням рівності. Тому даний трикутник є прямокутним трикутником.
Значення (3, 4 та 5) для натуральних чисел (a, b, c) відповідно - це комбінація чисел, відома як трійка Піфагора, які являють собою набір з трьох цілих чисел, які задовольняють теоремі Піфагора\(c^2=a^2+b^2\). Інші трійки Піфагора можуть бути згенеровані шляхом множення значень будь-якої відомої Піфагорійської Трійки на будь-яке додатне ціле число. Якщо значення (3, 4 і 5) помножити на 2, то створюється ще одна Піфагорейська трійка (6, 8 і 10). Якщо значення (6, 8 і 10) помножити на 4, то генерується ще одна трійка Піфагора (24, 32 і 40).
Нещодавно створені значення були замінені в теорему Піфагора, щоб переконатися\(c^2=a^2+b^2\), що вони є Піфагорійськими трійками.
\(\begin{align*} c^2&=a^2+b^2 &\qquad c^2&=a^2+b^2 \\ (10)^2&=(6)^2+(8)^2 &\qquad (40)^2&=(24)^2+(32)^2 \\ (10\times 10)&=(6\times 6)+(8\times 8)&\qquad (40\times 40)&=(24\times 24)+(32\times 32) \\ 100&=36+64&\qquad 1600&=576+1024 \\ 100&=100 &\qquad 1600&=1600\end{align*}\)
Кожна з нових трійок Піфагора призвела до\(c^2=a^2+b^2\) справжнього твердження рівності.
Якщо ви знаєте, що даний трикутник - це прямокутний трикутник, то теорема Піфагора може бути використана для обчислення довжини невідомої сторони трикутника, коли ви знаєте довжини двох сторін.
Давайте розглянемо приклад.
Для наступного прямокутного трикутника обчислити довжину невідомої сторони '\(b\)?'
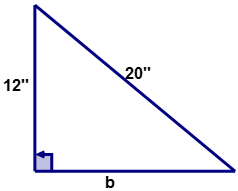
По-перше, використовуйте теорему Піфагора, щоб обчислити довжину сторони '\(b\).'
\(c^2= a^2+b^2\)
Далі заповніть значення, зазначені для сторін\(a\) 'і side'\(c\). '
\(\begin{align*}c^2&=a^2+b^2 \\ (20)^2&=(12)^2+b^2\end{align*}\)
Далі виконуємо зазначені операції.
\(\begin{align*}(20)^2&=(12)^2+b^2 \\ (20\times 20)&=(12\times 12)+b^2 \\ 400&=144+b^2\end{align*}\)
Далі відніміть 144 з обох сторін рівняння, щоб виділити змінну і спростити обидві сторони рівняння.
\(\begin{align*}400&=144+b^2 \\ 400−144&=144−144+b^2 \\ 256&=b^2\end{align*}\)
Потім вирішіть для 'b', взявши квадратний корінь обох сторін рівняння. Пам'ятайте, що взяття квадратного кореня - це зворотна операція квадратування.
\(\begin{align*}256&=b^2 \\ \sqrt{256}&=\sqrt{b^2} \\ 16&=b\end{align*}\)
Відповідь - 16.
Довжина сторони '\(b\)' становить 16 дюймів.
Приклад\(\PageIndex{1}\)
Раніше вам дали проблему про Трейсі та її рятувальну місію. Вона повинна знати, якщо сходи вона використовує досить довго, щоб врятувати свого кошеня.
Рішення
Спочатку намалюйте та позначте зображення, щоб змоделювати проблему.
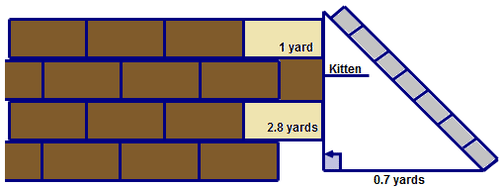
Далі подивіться на прямокутний трикутник і визначте виміри двох відомих сторін.
\(a=3.8\:yards\)
\(b=0.7\:yards\)
Далі використовуйте теорему Піфагора для обчислення довжини сходів, яка є гіпотенузою прямокутного трикутника.
\(c^2= a^2+b^2\)
Спочатку заповніть значення для «a» та «b».
\(\begin{align*}c^2&=a^2+b^2 \\ c^2&=(3.8)^2+(0.7)^2\end{align*}\)
Далі виконуємо зазначені операції і спрощуємо рівняння.
\(\begin{align*}c^2&=(3.8\times 3.8)+(0.7\times 0.7) \\ c^2&=14.44+0.49 \\ c^2&=14.93\:yards\end{align*}\)
Потім вирішіть для 'c', взявши квадратний корінь кожної сторони рівняння.
\(\begin{align*}c^2&=14.93 \\ \sqrt{c^2}&=\sqrt{14.93} \\ c&=3.86\end{align*}\)
Відповідь - 3,86.
Сходи повинні мати довжину 3,86 ярда, щоб врятувати кошеня. Сходи Трейсі використовує досить довго.
Приклад\(\PageIndex{2}\)
Використовуйте теорему Піфагора, щоб обчислити довжину відсутньої сторони наступного прямокутного трикутника:
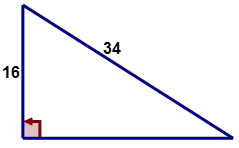
Рішення
Для початку визначте, що собою представляють дані значення і якої сторони не вистачає?
\(\begin{align*} a&=16 \\ b&=? \\ c&=34\end{align*}\)
Далі підставляємо задані значення в рівняння, яке представляє теорему Піфагора.
\(\begin{align*}c^2&=a^2+b^2 \\ (34)^2&=(16)^2+b^2\end{align*}\)
Далі виконуємо зазначені операції по обидва боки рівняння.
\(\begin{align*}(34)^2&=(16)^2+b^2 \\ (34\times 34)&=(16\times 16)+b^2 \\ 1156&=256+b^2\end{align*}\)
Далі відніміть 256 з обох сторін рівняння, щоб ізолювати змінну.
\(\begin{align*}1156&=256+b^2 \\ 1156−256&=256−256+b^2\end{align*}\)
Далі спрощуємо рівняння.
\(\begin{align*}1156−256&=256−256+b^2 \\ 900&=b^2\end{align*} \)
Потім візьміть квадратний корінь обох сторін рівняння, щоб вирішити для змінної '\(b\).'
\(\begin{align*} 900&=b^2 \\ \sqrt{900}&=\sqrt{b^2} \\ 30&=b\end{align*}\)
Відповідь є\(b=30\).
Приклад\(\PageIndex{3}\)
Знайти довжину гіпотенузи прямокутного трикутника, враховуючи, що довжини катетів\(a\) '' і «\(b\)'складають 14 і 48 сантиметрів відповідно.
Рішення
Спочатку намалюйте та позначте прямокутний трикутник, щоб представити задану інформацію.
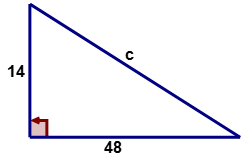
Далі підставляємо задані значення в рівняння, яке представляє теорему Піфагора.
\(\begin{align*} c^2&= a^2+b^2 \\ c^2&= (14)^2+(48)^2\end{align*}\)
Далі виконуємо зазначені операції і спрощуємо рівняння.
\(\begin{align*} c^2= (14)^2+(48)^2 \\ c^2&= (14\times 14)+(48\times 48) \\ c^2&= 196+2304\end{align*} \)
Далі спростіть рівняння, склавши значення в правій частині рівняння.
\(\begin{align*} c^2&= 196+2304 \\ c^2&= 2500\end{align*}\)
Потім візьміть квадратний корінь обох сторін рівняння, щоб вирішити для змінної '\(c\).'
\(\begin{align*} c^2&= 2500 \\ \sqrt{c^2}&=2500 \\ c&=50\end{align*}\)
Відповідь є\(c=50\).
Довжина гіпотенузи - 50 см.
Приклад\(\PageIndex{4}\)
Якщо '\(a\)' і '\(b\)' - це такі значення, що\(a,\:b\in N\) і\(a>b\) потім сторони прямокутного трикутника\(a^2+b^2\)\(a^2−b^2\), і\(2ab\) як показано на схемі нижче.
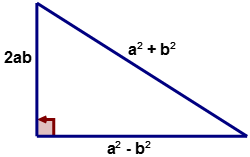
Рішення
Заповніть наступну таблицю, щоб створити трійки Піфагора.
| \ (ав | \( b\) | \(a^2−b^2\) | \(2ab\) | \(a^2+b^2\) |
| 4 | 2 | 12 | 16 | 20 |
| 5 | 3 | 16 | 30 | 34 |
| 6 | 4 | 20 | 48 | 52 |
По-перше, використовуючи\(a=4 and \(b=2\) обчислення\(a^2−b^2\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &a^2−b^2 \\ &(4)^2−(2)^2\end{align*}\)
Далі виконуємо зазначені операції і просто вираз.
\(\begin{align*} &(4)^2−(2)^2 \\ &(4\times 4)−(2\times 2) \\ &16−4 \\ &12\end{align*} \)
Відповідь - 12.
Потім помістіть відповідь в таблицю в правильному стовпці.
Тепер заповніть\(a^2−b^2\) стовпець для решти заданих значень\(a\) '' і '\(b\).
По-перше, використовуючи\(a=5\) та\(b=3\) оцінюйте\(a^2−b^2\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &a^2−b^2 \\ &(5)^2−(3)^2\end{align*} \)
Далі виконуємо зазначені операції і просто вираз.
\(\begin{align*} (5)^2−(3)^2 \\ (5\times 5)−(3\times 3) \\ 25−9=16\end{align*} \)
Відповідь - 16.
Потім помістіть відповідь в таблицю в правильному стовпці.
По-перше, використовуючи\(a=6\) та\(b=4\) оцінюйте\(a^2−b^2\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &a^2−b^2 \\ &(6)^2−(4)^2 \end{align*}\)
Далі виконуємо зазначені операції і просто вираз.
\(\begin{align*} (6)^2−(4)^2 \\ &(6\times 6)−(4\times 4) \\ &36−16 \\ &20 \end{align*} \)
Відповідь - 20.
Потім помістіть відповідь в таблицю в правильному стовпці.
По-перше, використовуючи\(a=4\) та\(b=2\) оцінюйте\(2ab\) шляхом підстановки заданих значень у вираз.
\(2ab\)
\(2(4)(2)\)
Далі виконуємо зазначені операції.
\(2(4)(2)\)
\(8(2)\)
\(16\)
Відповідь - 16.
Потім помістіть відповідь в таблицю в правильному стовпці.
Тепер заповніть\(2ab\) стовпець для решти заданих значень\(a\) '' і '\(b\).
По-перше, використовуючи\(a=5\) та\(b=3\) оцінюйте\(2ab\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &2ab \\ &2(5)(3)\end{align*}\)
Далі виконуємо зазначені операції.
\(\begin{align*} &2(5)(3) \\ &10(3) \\ &30\end{align*}\)
Відповідь - 30.
Потім помістіть відповідь в таблицю в правильному стовпці.
По-перше, використовуючи\(a=6\) та\(b=4\) оцінюйте\(2ab\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &2ab \\ &2(6)(4)\end{align*}\)
Далі виконуємо зазначені операції.
\(\begin{align*}&2(6)(4) \\ &12(4) \\ &48\end{align*}\)
Відповідь - 48.
Потім помістіть відповідь в таблицю в правильному стовпці.
По-перше, використовуючи\(a=4\) та\(b=2\) оцінюйте\(a^2+b^2\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &a^2+b^2 \\ &(4)^2(2)^2\end{align*} \)
Далі виконуємо зазначені операції і просто вираз.
\(\begin{align*} &(4)^2+(2)^2 \\ &(4\times 4)+(2\times 2)16+4 \\ &20\end{align*}\)
Відповідь - 20.
Потім помістіть відповідь в таблицю в правильному стовпці.
Тепер заповніть\(a^2+b^2\) стовпець для решти заданих значень\(a\) '' і '\(b\).
По-перше, використовуючи\(a=5\) та\(b=3\) оцінюйте\(a^2+b^2\) шляхом підстановки заданих значень у вираз.
\(\begin{align*} &a^2+b^2 \\ &(5)^2+(3)^2\end{align*}\)
Далі виконуємо зазначені операції і просто вираз.
\( \begin{align*} &(5)^2+(3)^2 \\ &(5\times 5)+(3\times 3) \\ &25+9 \\ &34 \end{align*}\)
Відповідь 34.
Потім помістіть відповідь в таблицю в правильному стовпці.
По-перше, використовуючи\(a=6\) та\(b=4\) оцінюйте\(a^2+b^2\) шляхом підстановки заданих значень у вираз.
\(a^2+b^2\)
\((6)^2+(4)^2\)
Далі виконуємо зазначені операції і просто вираз.
\(\begin{align*} &(6)^2+(4)^2 \\ &(6\times 6)+(4\times 4) \\ &36+16 \\ &52\end{align*}\)
Відповідь - 52.
Потім помістіть відповідь в таблицю в правильному стовпці.
Приклад\(\PageIndex{5}\)
Використовуйте теорему Піфагора, щоб знайти довжину відсутньої ніжки наступного прямокутного трикутника.
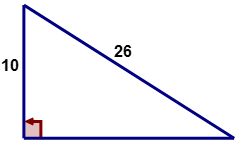
Рішення
Для початку визначте, що собою представляють дані значення і якої сторони не вистачає?
\(\begin{align*} a&=? \\ b&=10 \\ c&=26\end{align*} \)
Далі підставляємо задані значення в рівняння, яке представляє теорему Піфагора.
\(\begin{align*} c^2&=a^2+b^2 \\ (26)^2&=a^2+(10)^2\end{align*}\)
Далі виконуємо зазначені операції і спрощуємо рівняння.
\(\begin{align*} (26)^2&=a^2+(10)^2 \\ (26\times 26)&=a^2+(10\times 10) \\ 676&=a^2+100\end{align*}\)
Далі відніміть 100 з обох сторін рівняння, щоб ізолювати змінну.
\(\begin{align*} 676&=a^2+100 \\ 676−100&=a^2+100−100 \end{align*} \)
Далі спрощуємо рівняння.
\(\begin{align*} 676−100&=a^2+100−100 \\ 576&=a^2\end{align*}\)
Потім візьміть квадратний корінь обох сторін рівняння, щоб вирішити для змінної 'a'.
\(\begin{align*}576&=a^2 \\ \sqrt{576}&=\sqrt{a^2} \\ 24&a\end{align*}\)
Відповідь є\(a=24\).
Рецензія
Використовуйте теорему Піфагора, щоб знайти відсутні розміри кожного прямокутного трикутника.
- \(a=3,\:b=4,\:c=?\)
- \(a=6,\:b=8,\:c=?\)
- \(a=9,\:b=12,\:c=?\)
- \(a=27,\:b=36,\:c=?\)
- \(a=15,\:b=20,\:c=?\)
- \(a=18,\:b=24,\:c=?\)
- \(a=?,\:b=16,\:c=20\)
- \(a=?,\:b=28,\:c=35\)
- \(a=30,\:b=?,\:c=50\)
- \(a=33,\:b=?,\:c=55\)
- \(a=1.5,\:b=?,\:c=2.5\)
- \(a=36,\:b=?,\:c=60\)
Вкажіть, чи є наступні твердження True або False.
- Теорема Піфагора буде працювати для будь-якого трикутника.
- Найдовша сторона прямокутного трикутника називається гіпотенузою.
- Піфагорійську трійку можна знайти тільки в прямокутному трикутнику.
Лексика
| Термін | Визначення |
|---|---|
| Гіпотенуза | Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута. |
| Ніжки прямокутного трикутника | Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута. |
| Теорема Піфагора | Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана\(a^2+b^2=c^2\), де a і b - катети трикутника, а c - гіпотенуза трикутника. |
| Піфагор Потрійний | Піфагорійська трійка - це набір з трьох цілих чисел a, b і c, які задовольняють теоремі Піфагора,\(a^2+b^2=c^2\). |
| Правий трикутник | Прямокутний трикутник - це трикутник з одним кутом 90 градусів. |
Додаткові ресурси
Відео: Теорема Піфагора 2
Практика: Основи теореми Піфагора
Реальний світ: вимірювання світу