4.27: Теорема Піфагора

Last updated

Oct 27, 2022
Save as PDF
- 4.26: Теорема нерівності трикутника
- 4.28: Основи теореми Піфагора

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Квадрат гіпотенузи дорівнює сумі квадратів катетів у прямих трикутниках.

Дві коротші сторони прямокутного трикутника (сторони, що утворюють прямий кут) - катети, а довша сторона (сторона, протилежна прямому куту) - гіпотенуза. Для теореми Піфагора катети « $a$ » і « $b$ », а гіпотенуза - « $c$ ».

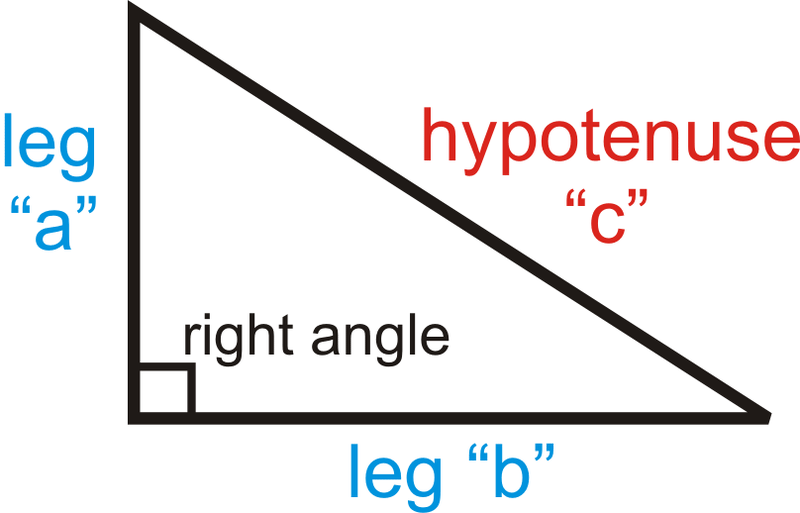
F-д_FF8Е 77018348E250DC CC070A9E8DE01ed5A96304AF3A84DB2C87DC2B5+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Теорема Піфагора: Дано прямокутний трикутник з катетами довжин a і b і гіпотенузою довжини $c$ , $a^2+b^2=c^2$ .

Зворотне значення теореми Піфагора також вірно. Це дозволяє довести, що трикутник - це прямокутний трикутник, навіть якщо ви не знаєте його кутових вимірювань.

Теорема Піфагора Converse: Якщо квадрат найдовшої сторони трикутника дорівнює сумі квадратів двох інших сторін, то трикутник є прямокутним трикутником.

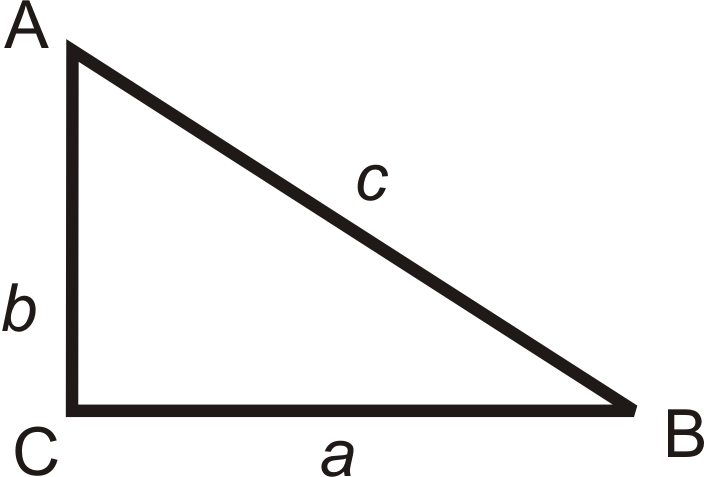
Якщо $a^2+b^2=c^2$ , то $\Delta ABC$ це прямокутний трикутник.

F-д_Е9 БДДДК 7Ф2ДФ 04221А373153 Бібе 53575131c800c31ad42AC0B5A860+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Піфагорійська трійка

Комбінація з трьох чисел, яка робить теорему Піфагора істинною, називається трійкою Піфагора. Кожен набір чисел нижче - це піфагорійська трійка.

$3,4,5 \qquad 5,12,13\qquad 7,24,25\qquad 8,15,17\qquad 9,12,15\qquad 10,24,26$

Будь-яка кратна трійці Піфагора також вважається трійкою Піфагора. Множення 3, 4, 5 на 2 дає 6, 8, 10, що є ще однією трійкою. Щоб побачити, чи набір чисел робить трійку Піфагора, підключіть їх до теореми Піфагора.

Що робити, якщо вам сказали, що трикутник має довжину сторін 5, 12 і 13? Як ви могли визначити, чи трикутник був правильним?

Приклад $\PageIndex{1}$

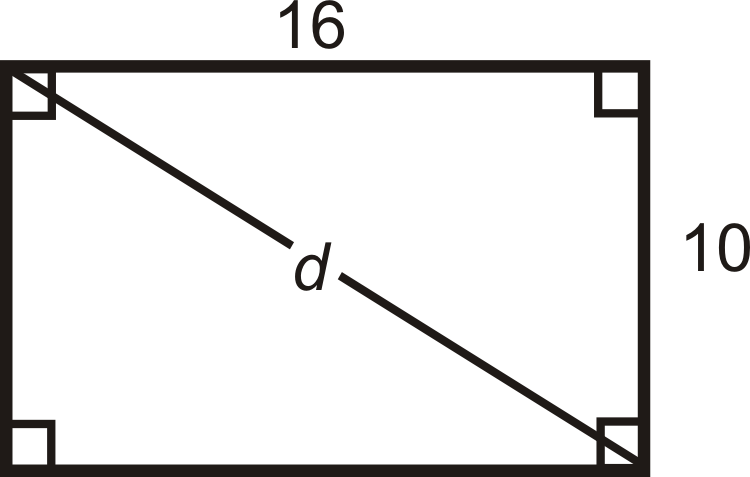
Яка діагональ прямокутника зі сторонами 10 і 16?

F-D_14518172455B АБ 3Б916Б9Е747 БББ 119ФДА86ФА9Д9С8С99Ф1А3Д9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Рішення

Для будь-якого квадрата і прямокутника можна використовувати теорему Піфагора, щоб знайти довжину діагоналі. Підключіть в сторони, щоб знайти $d$ .

$\begin{align*} 10^2+16^2=d^2 \\ 100+256=d^2 \\ 356&=d^2 \\ d&=\sqrt{356}=2\sqrt{89}\approx 18.87 \end{align*}$

Приклад $\PageIndex{2}$

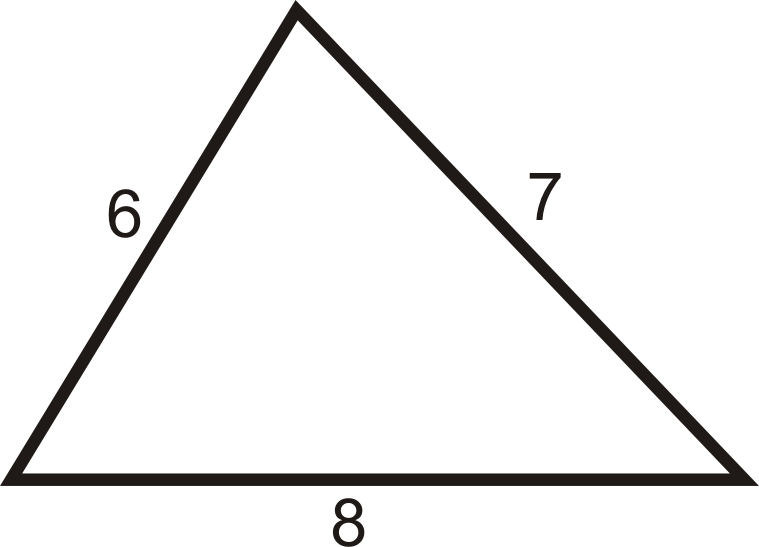
Чи роблять 6, 7 і 8 сторони прямокутного трикутника?

F-д_501608ББА 780954A047b06C4145b889ec24c64836e99FF2FE9A137C4+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Рішення

Підключіть три числа до теореми Піфагора. Пам'ятайте, що найбільшою довжиною завжди буде гіпотенуза, c. якщо $6^2+7^2=8^2$ , то вони є сторонами прямокутного трикутника.

$\begin{align*} 6^2+7^2&=36+49=85& \\ 8^2&=64&\qquad 85 \neq 64,\: so\: the \:lengths \:are \:not \:the \:sides \:of \:a \:right \:triangle.\end{align*}$

Приклад $\PageIndex{3}$

Знайти довжину гіпотенузи.

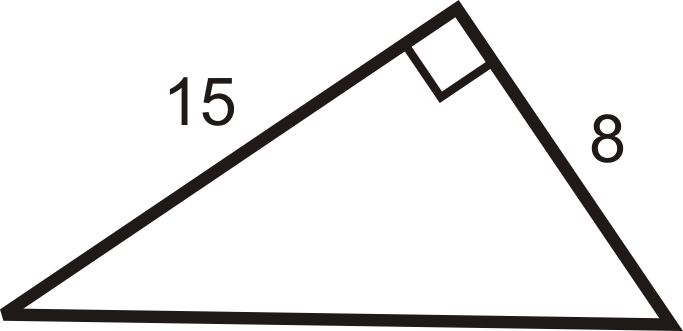
F-д_Е316792 А160 Ад Б47Е08ЕД 37096Е6592Д5571С63ЕД 3E788D353B98F8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рішення

Використовуйте теорему Піфагора. Набір $a=8$ і $b=15$ . Вирішити для $c$ .

$\begin{align*} 8^2+152&=c^2 \\ 64+225&=c^2 \\ 289&=c^2 \qquad Take\: the \:square \:root \:of \:both \:sides. \\ 172&=c\end{align*}$

Приклад $\PageIndex{4}$

Чи є 20, 21, 29 піфагорійською трійкою?

Рішення

Якщо $20^2+21^2=29^2$ , то множина - це піфагорійська трійка.

$\begin{align*} 20^2+21^2&=400+441=841 \\ 29^2&=841 \end{align*}$

Тому 20, 21 і 29 - це піфагорійська трійка.

Приклад $\PageIndex{5}$

Визначте, чи трикутники нижче є прямими трикутниками.

Перевірте, чи задовольняють три довжини теоремі Піфагора. Нехай найдовша сторона представляє c.

Рішення

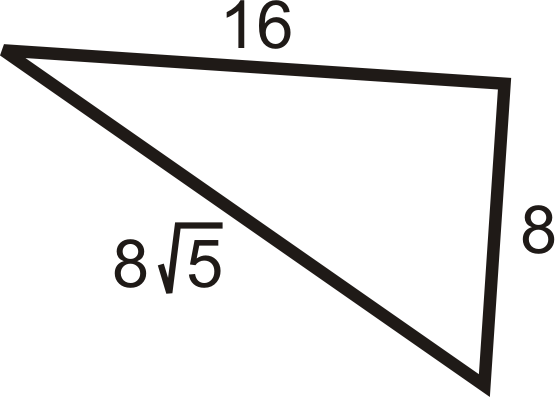
Малюнок $\PageIndex{6}$

$\begin{align*} a^2+b^2&=c^2 \\ 82+162 &\stackrel{?}{=}(8\sqrt{5})2 \\ 64+256 &\stackrel{?}{=}64\cdot 5 \\ 320&=320\qquad Yes\end{align*}$

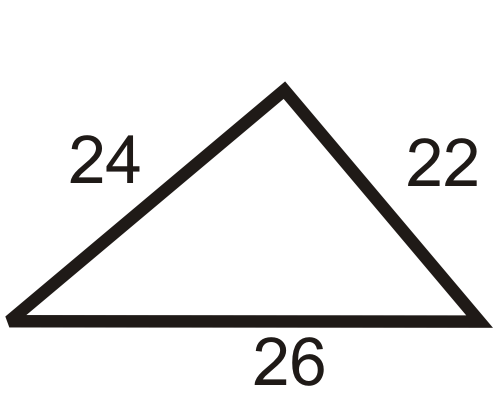
Малюнок $\PageIndex{7}$

$\begin{align*} a^2+b^2&=c^2 \\ 22^2+24^2&\stackrel{?}{=}262 \\ 484+576 &\stackrel{?}{=}676 \\ 1060 &\neq 676\qquad No\end{align*}$

Рецензія

Знайдіть довжину відсутньої сторони. Спрощення всіх радикалів.

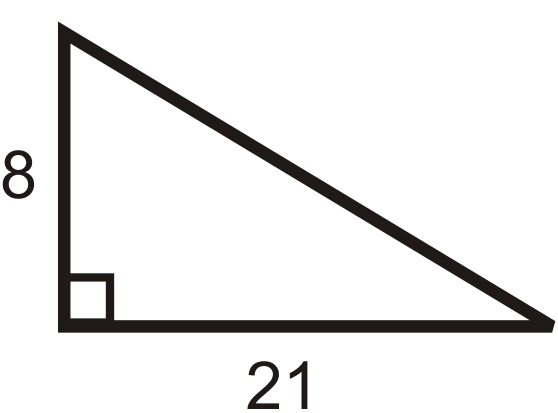
Малюнок $\PageIndex{8}$
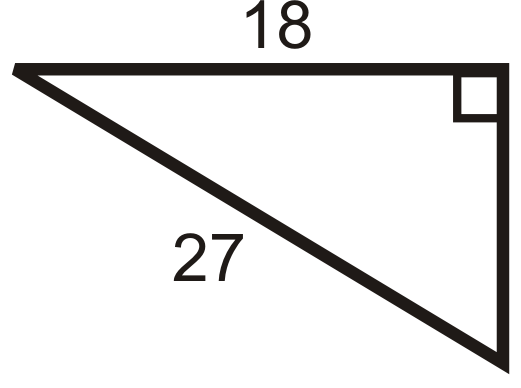
Малюнок $\PageIndex{9}$
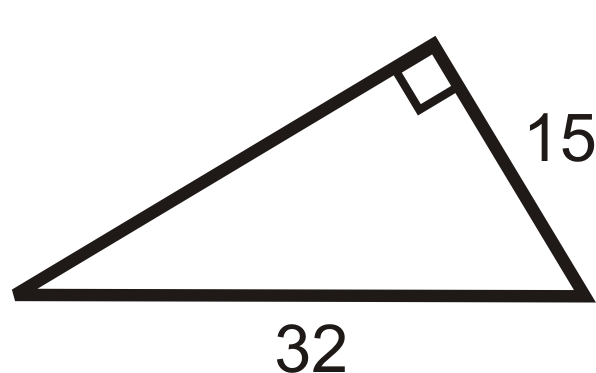
Малюнок $\PageIndex{10}$
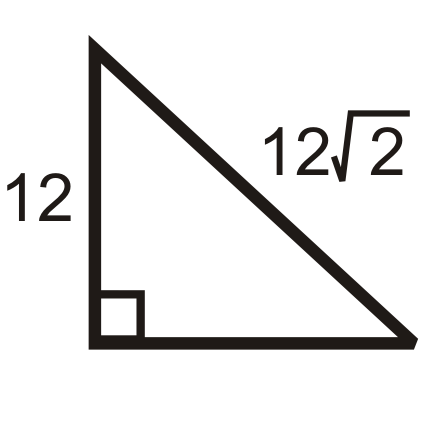
Малюнок $\PageIndex{11}$
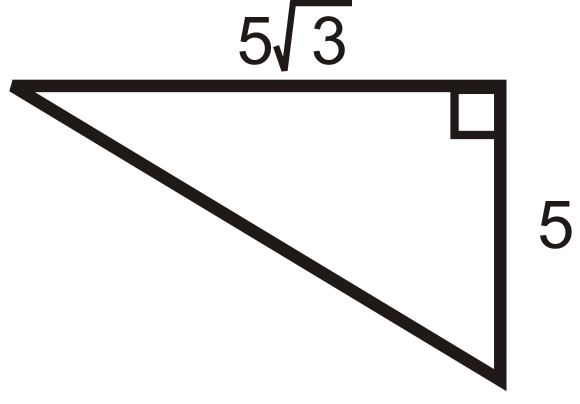
Малюнок $\PageIndex{12}$
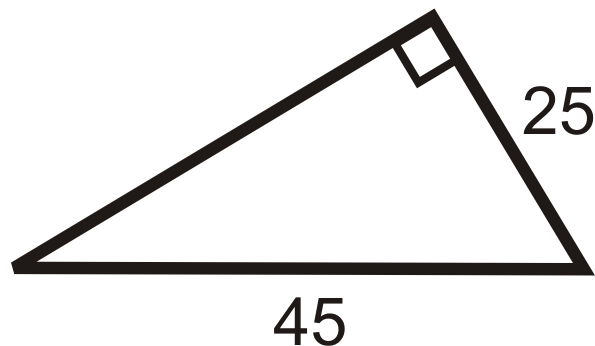
Малюнок $\PageIndex{13}$
Якщо катети прямокутного трикутника 10 і 24, то гіпотенуза дорівнює __________.
Якщо сторони прямокутника 12 і 15, то діагональ - _____________.
Якщо сторін квадрата 16, то діагональ - ____________.
Якщо сторін квадрата 9, то діагональ - _____________.

Визначте, чи є наступні набори чисел Піфагорійськими трійками.

12, 35, 37
9, 17, 18
10, 15, 21
11, 60, 61
15, 20, 25
18, 73, 75

Визначте, чи роблять наступні довжини прямокутний трикутник.

7, 24, 25
$\sqrt{5},2\sqrt{10},3\sqrt{5}$
$2\sqrt{3},\sqrt{6},8$
15, 20, 25
20, 25, 30
$8\sqrt{3},6,2\sqrt{39}$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.2.

Лексика

Термін	Визначення
Теорема Піфагора	Теорема Піфагора - це математична залежність між сторонами прямокутного трикутника, задана $a^2+b^2=c^2$ , де a і b - катети трикутника, а c - гіпотенуза трикутника.
Піфагорійська трійка	Комбінація з трьох чисел, яка робить теорему Піфагора істинною.
Коло	Коло - це сукупність всіх точок на певній відстані від заданої точки в двох вимірах.
Конічна	Конічні перерізи - це ті криві, які можуть бути створені перетином подвійного конуса і площини. Вони включають кола, еліпси, параболи та гіперболи.
вироджений конічний	Вироджена конічна коніка - це конічний, який не має звичних властивостей конічного перерізу. Оскільки деякі коефіцієнти загального конічного рівняння дорівнюють нулю, то базовою формою коніки є просто точка, пряма або пара пересічних ліній.
Еліпс	Еліпси - це конічні зрізи, які мають вигляд витягнутих кіл. Еліпс представляє всі місця в двох вимірах, які знаходяться на однаковій відстані від двох заданих точок, які називаються вогнищами.
гіпербола	Гіпербола - це конічний переріз, утворений, коли січна площина перетинає обидві сторони конуса, в результаті чого утворюються дві нескінченні «U» -образні криві.
Гіпотенуза	Гіпотенуза прямокутного трикутника - найдовша сторона прямокутного трикутника. Вона знаходиться поперек від прямого кута.
Ніжки прямокутного трикутника	Ніжки прямокутного трикутника - це дві коротші сторони прямокутного трикутника. Ноги примикають до прямого кута.
Парабола	Парабола - це характерна форма квадратичного графіка функції, що нагадує «U».
Піфагорейське число потрійне	Піфагорійська трійка - це набір з трьох цілих чисел a, b і c, які задовольняють теоремі Піфагора, $a^2+b^2=c^2$ .
Правий трикутник	Прямокутний трикутник - це трикутник з одним кутом 90 градусів.

Додаткові ресурси

Інтерактивний елемент

Відео: Використання принципів теореми Піфагора - Основні

Види діяльності: Теорема Піфагора та Піфагорейська трійка Дискусійні питання

Навчальні посібники: Посібник з вивчення теореми Піфагора

Практика: Теорема Піфагора

Реальний світ: Піфагор ТВ