Skip to main content
LibreTexts - Ukrayinska

4.25: Порівняння кутів і сторін у трикутниках

  1. Last updated
  2. Save as PDF
  • Page ID
    54829

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Теореми нерівності та впорядкування кутів і сторін трикутників.

    Теореми про нерівність SAS та SSS

    Подивіться на трикутник нижче. Задано сторони трикутника. Чи можете ви визначити, який кут найбільший? Найбільший кут буде протилежним 18, тому що це найдовша сторона. Аналогічно найменший кут буде протилежним 7, що є найкоротшою стороною.

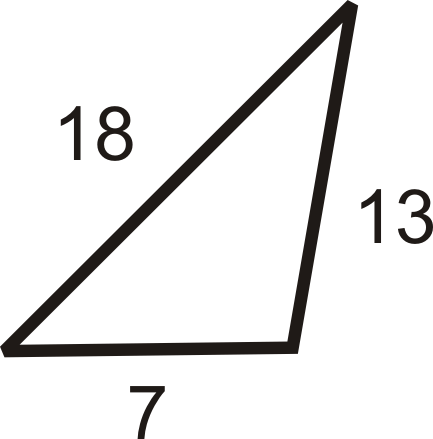
    F-д_9д7 БФ 56ДК61А8259821813701292ФДА0170440558БА00Ф8Б2С01434+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Ця ідея насправді є теоремою: якщо одна сторона трикутника довша за іншу сторону, то кут, протилежний довшій стороні, буде більше, ніж кут, протилежний коротшій стороні.

    Зворотне також вірно: якщо один кут у трикутнику більший за інший кут у цьому трикутнику, то сторона, протилежна більшому куту, буде довшою, ніж сторона, протилежна меншому куту.

    Ми можемо розширити цю ідею на дві теореми, які допомагають нам порівняти сторони і кути в двох трикутників Якщо у нас є два конгруентні трикутники\(\Delta ABC\) і\(\Delta DEF\), позначені нижче:

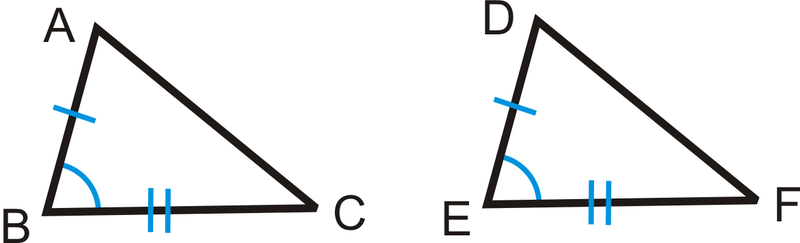
    Ф-Д_Е22ДЭ10Б 76А8 КД0С333С7936 БЕ8А05Ф7931А026Б2С4А98574БФ7Б92+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Тому якщо\(AB=DE\)\(BC=EF\), і\(m\angle B=m\angle E\), то\(AC=DF\).

    Тепер давайте зробимо\(m\angle B>m\angle E\). Це зробило б\(AC>DF\)? Так. Ця ідея називається теоремою нерівності SAS.

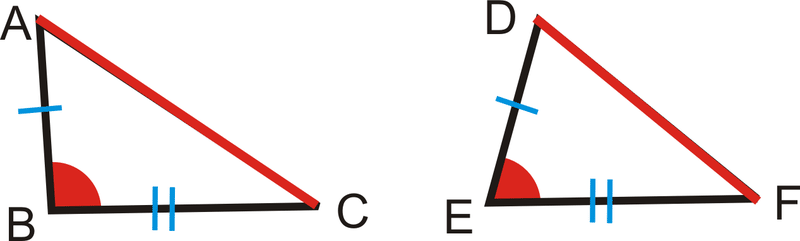
    F-д_89 ЕБ6Ф663Е70777394Д7112ФБД627ЕЕЕЕБ7Б6А1де4Е0Ф5300220561+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Теорема нерівності SAS: Якщо дві сторони трикутника конгруентні двом сторонам іншого трикутника, але включений кут одного трикутника має більшу міру, ніж включений кут іншого трикутника, то третя сторона першого трикутника довша за третю сторону другого трикутник.

    F-д_89 ЕБ6Ф663Е70777394Д7112ФБД627ЕЕЕЕБ7Б6А1де4Е0Ф5300220561+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Якщо\(\overline{AB}\cong \overline{DE}\),\(\overline{BC}\cong \overline{EF}\) і\(m\angle B>m\angle E\), то\(\overline{AC}>\overline{DF}\).

    Якщо ми знаємо треті сторони на відміну від кутів, протилежна ідея також вірна і називається теоремою нерівності SSS.

    Теорема про нерівність SSS: Якщо дві сторони трикутника конгруентні двом сторонам іншого трикутника, але третя сторона першого трикутника довша, ніж третя сторона другого трикутника, то включений кут двох конгруентних сторін першого трикутника більше за мірою, ніж включений кут двох конгруентних сторін другого трикутника.

    F-д_89 ЕБ6Ф663Е70777394Д7112ФБД627ЕЕЕЕБ7Б6А1де4Е0Ф5300220561+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Якщо\(\overline{AB}\cong \overline{DE}\),\(\overline{BC}\cong \overline{EF}\) і\(\overline{AC}>\overline{DF}\), то\( m\angle B>m\angle E\).

    Що робити, якщо вам сказали, що трикутник має сторони, які вимірюють 3, 4 і 5? Як ви могли визначити, який з кутів трикутника найбільший? Найменший?

    Приклад\(\PageIndex{1}\)

    Якщо\(\overline{XM}\) є медіаною\(\Delta XYZ\) і\(XY>XZ\), що ми можемо сказати про\(m\angle 1\) і\(m\angle 2\)?

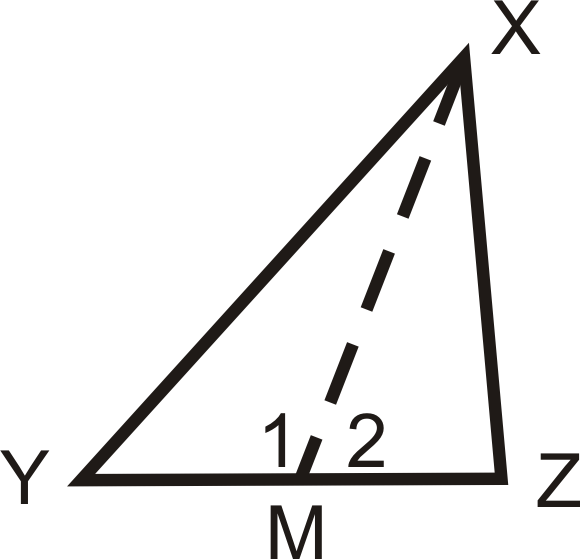
    F-д_89А 2ББ 32168С42КБ88А0Б6С 94Б00Е366Е1Б17Д4С045С72Ф18199Б2Б2Б+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    М - середина\(\overline{YZ}\), так що\(YM=MZ\). \(MX=MX\)Рефлексивним майном, і ми знаємо\(XY>XZ\).

    Ми можемо використовувати теорему нерівності SSS Converse сказати\(m\angle 1>m\angle 2\).

    Приклад\(\PageIndex{2}\)

    Внизу - рівнобедрений трикутник\(\Delta ABC\). Перерахуйте все, що ви можете про сторони і кути трикутника і чому.

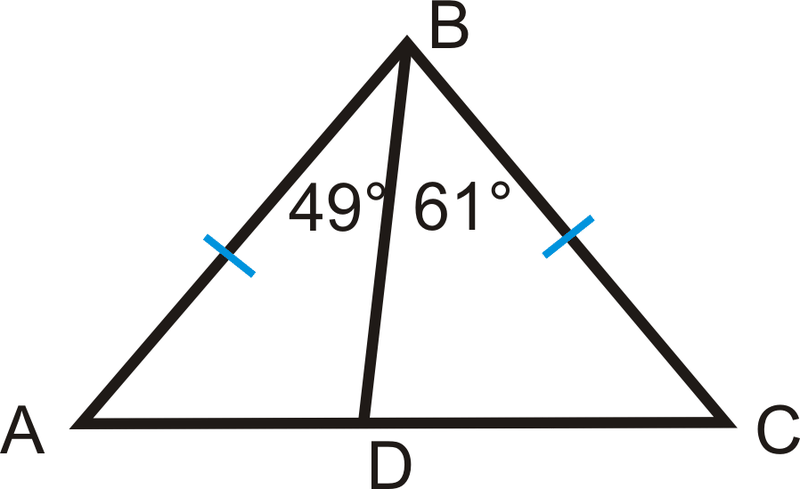
    F-д_487Б821Б133ФА4ДБ6Б65316СБ 48Е43Б58ЕФ2Б452А78Б5ФЕ1408Б6Ф6+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Рішення

    М - середина\(\overline{YZ}\), так що\(YM=MZ\). \(MX=MX\)Рефлексивним майном, і ми знаємо\(XY>XZ\).

    \(AB=BC\)тому що це дано.

    \(m\angle A=m\angle C\)тому що якщо сторони рівні, то їх протилежні кути повинні бути рівні..

    \(AD<DC\)тому що\(m\angle ABD<m\angle CBD\) і через теорему нерівності трикутника SAS.

    Приклад\(\PageIndex{3}\)

    Перерахуйте сторони по порядку, від найкоротшої до найдовшої.

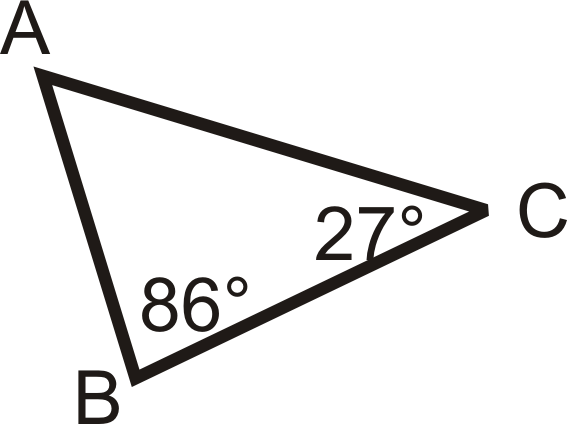
    F-D_92CBA 677Б437 ФД4Д55Е09С240Д59С0С43229809С043А24Б 650C3D0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)

    Рішення

    Спочатку знайдіть m\ кут A з теореми про суму трикутника:

    \(\begin{align*} m\angle A+86^{\circ}+27^{\circ}&=180^{\circ} \\ m\angle A&=67^{\circ} \end{align*}\)

    \(86^{\circ}\)є найбільшим кутом, тому\(AC\) є найдовшою стороною. Наступний кут\(67^{\circ}\), так\(BC\) буде наступна довша сторона. \(27^{\circ}\)є найменшим кутом, так\(AB\) є найкоротша сторона. По порядку, відповідь така:\(AB\),\(BC\),\(AC\).

    Приклад\(\PageIndex{4}\)

    Перерахуйте кути по порядку, від найбільших до найменших.

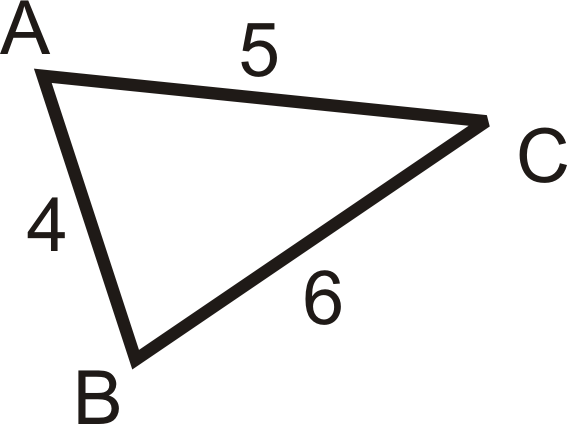
    F-д_Е5 СБ04Ф3174А4А4А007АААА0С 0ФК 12С16945361Е38А5476Б833C8C5E2269+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)

    Рішення

    Так само, як і у сторін, найбільший кут знаходиться навпроти найдовшої сторони. Найдовша сторона\(BC\), тому найбільший кут є\(\angle A\). Далі буде\(\angle B\) і тоді\(\angle C\).

    Приклад\(\PageIndex{5}\)

    Перерахуйте сторони по порядку, від найменшого до найбільшого.

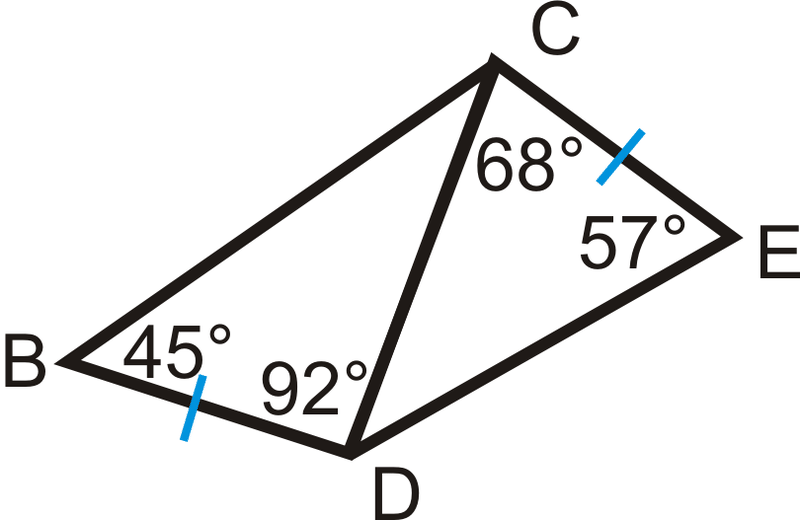
    F-D_3DBE09822 Додати 921д67А57Б456Ф8609ДК09ФБ83А042663139994898A9+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)

    Рішення

    Для вирішення давайте почнемо з\ Delta DCE\). Відсутній кут є\(55^{\circ}\). За теоремою, представленої в цьому розділі, сторони, по порядку від найменшого до найбільшого\(CE\), є\(CD\), і\(DE\).

    Бо\(\Delta BCD\), відсутній кут є\(43^{\circ}\). Знову ж таки, за теоремою, представленої в цьому розділі, порядок сторін від найменшого до найбільшого\(BD\) дорівнює\(CD\), і\(BC\).

    За теоремою нерівності SAS ми знаємо\(BC>DE\), що, таким чином, порядок всіх сторін буде:\(BD\),\(CE\),\(CD\),\(DE\),\(BC\).

    Рецензія

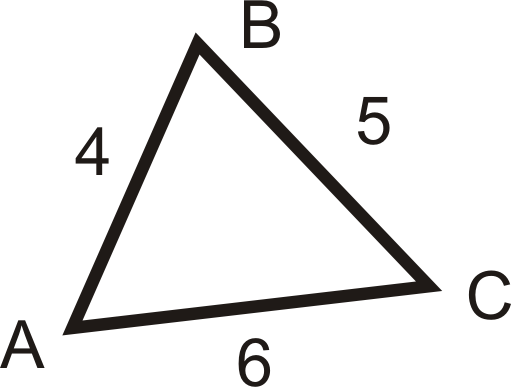
    Для питань 1-3 перерахуйте сторони по порядку від найкоротшого до найдовшого.

    1. F-д_6Е65БА 10Б618 Ф 91ЕФ277C1d4C0АЦ596Ф2909ЕФА 43 ЕФ47Б538+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
    2. F-D_A1146815E1754 ЕДА 16ЕБ02С47ЕБ5КС9Е7927КФС86299Б73Е80АС7Б5С+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
    3. F-д_7 баеф 8Ф9 ЕЕБ 39089 ЕБА 63А549Б83А2 ББ6Д0А01 ФЕФ 9АА92С748Б0517+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)

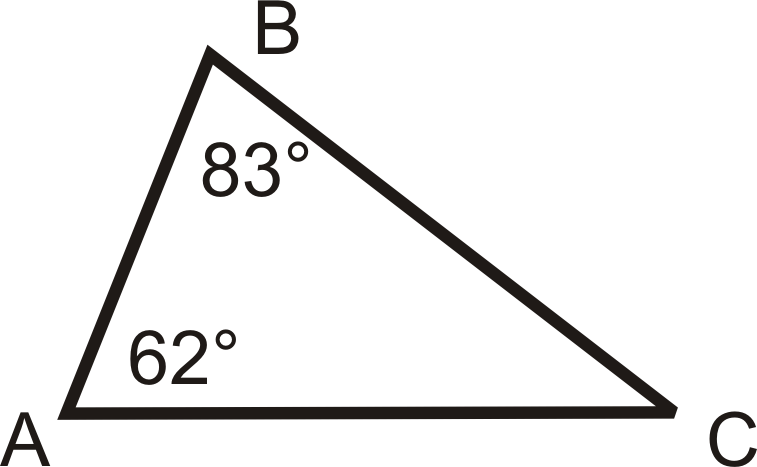
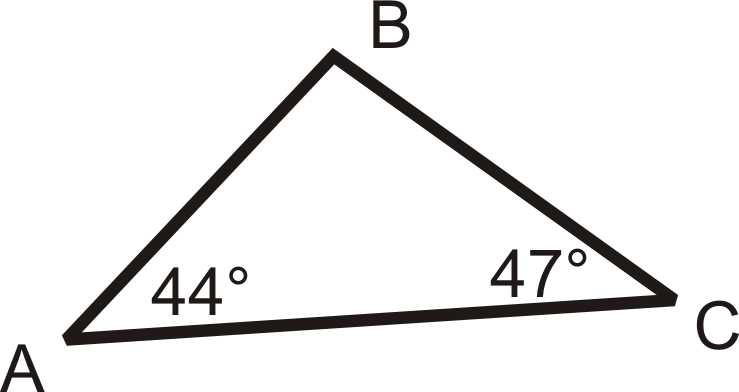
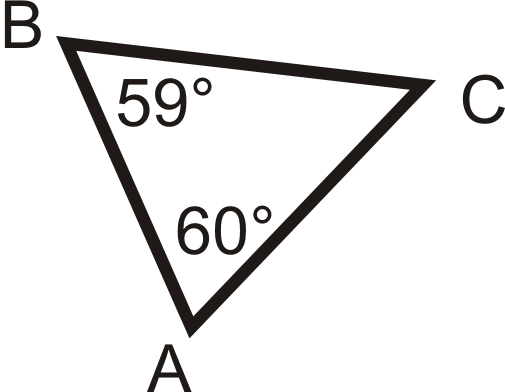
    Для питань 4-6 перерахуйте кути від найбільшого до найменшого.

    1. F-д_Д99С14Ф43Б1106 ЕЕ6С98Д6АБ2Д9858Д2485Б684ДД16563С0Е05Б8А28+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
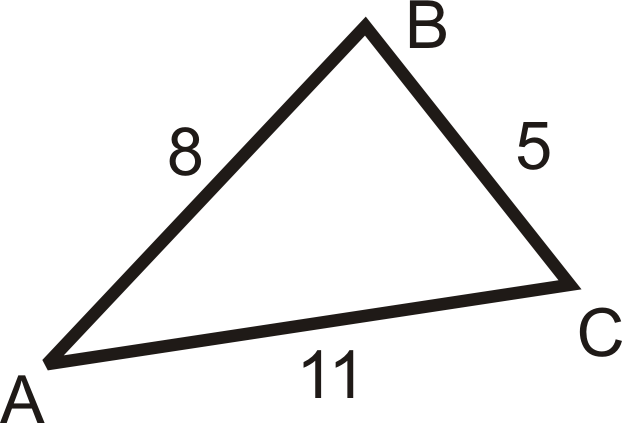
    2. F-д_5653д37д6155д3Д3ЕЦ5Б4749213b2EE59C7921402d2d3d3613C63D92+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
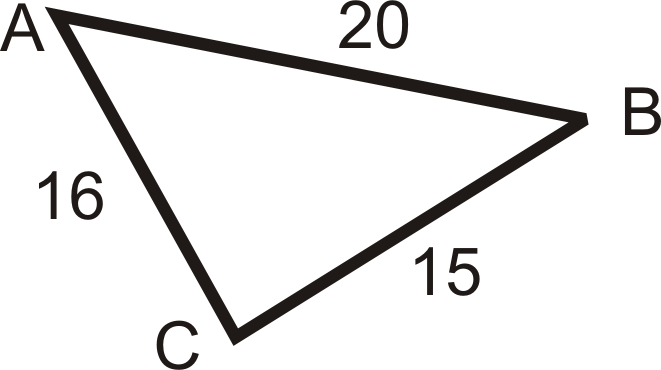
    3. F-D_9993C95С85Б7711A3 САА2Е26Е9Б20Б0Е7АД 859D9DE1C432E0d+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
    4. Намалюйте трикутник зі сторонами 3 см, 4 см і 5 см. Вимірювання кута є\(90^{\circ}\)\(53^{\circ}\),, і\(37^{\circ}\). Розмістіть кутові заходи у відповідних місцях.
    5. Намалюйте трикутник з кутовими мірками\(56^{\circ}\),\(54^{\circ}\) а включена сторона - 8 см. Яка найдовша сторона цього трикутника?
    6. Намалюйте трикутник зі сторонами 6 см, 7 см і 8 см. Вимірювання кута є\(75.5^{\circ}\)\(58^{\circ}\),, і\(46.5^{\circ}\). Розмістіть кутові заходи у відповідних місцях.
    7. Які висновки можна зробити\(x\)?
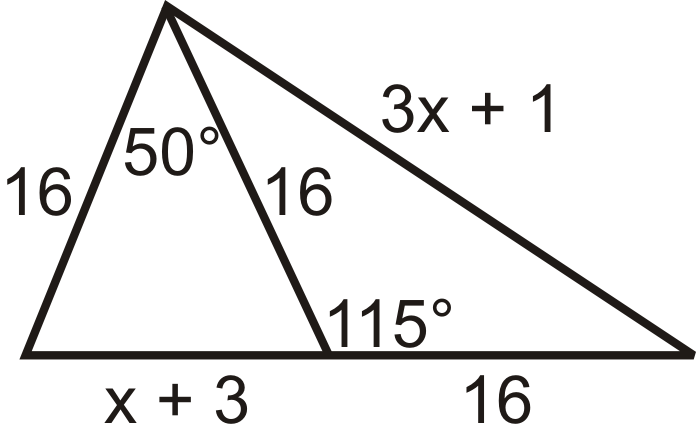
      F-д_9А 53Е5д 7619Б950907А90518 СА621СЕ 20ЕСФА8Б0ФД3ДД4130651Б558+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{17}\)
    8. Порівняйте\(m\angle 1\) і\(m\angle 2\).
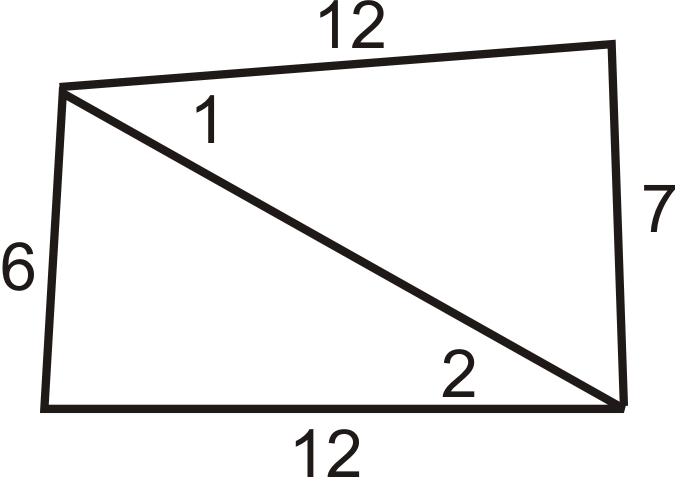
      F-D_CF41854996870023Е 300Б6А32Д5184Б182Ф98448 КК88Е887Д2АФ688+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{18}\)
    9. Перерахуйте сторони від найкоротшої до найдовшої.
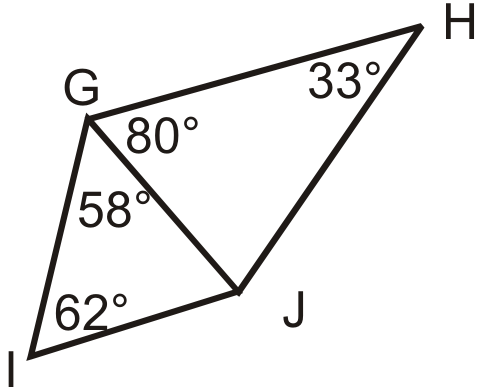
      Ф-Д_9Ф9Ф857С10083110Б50 АЕ 48 ЕБКА0ФФА0ФКД 832БФ 63053Ф76364C8C+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{19}\)
    10. Порівняйте\(m\angle 1\) і\(m\angle 2\). Що можна сказати про\(m\angle 3\) і\(m\angle 4\)?
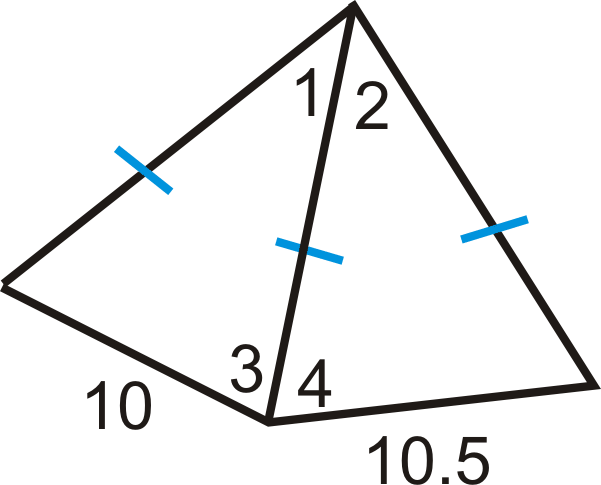
      Ф-д_1де 892 Б0776 Ф3827116962Б35Е4557Д6А12350980Б0ФЧ 8660208949A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{20}\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.6.

    Ресурси

    Лексика

    Термін Визначення
    Теорема про нерівність SAS Теорема нерівності SAS стверджує, що якщо дві сторони трикутника конгруентні двом сторонам іншого трикутника, але включений кут одного трикутника має більшу міру, ніж включений кут іншого трикутника, то третя сторона першого трикутника довша, ніж третя сторона другого трикутника .
    Теорема про нерівність SSS Теорема про нерівність SSS стверджує, що якщо дві сторони трикутника конгруентні двом сторонам іншого трикутника, але третя сторона першого трикутника довша за третю сторону другого трикутника, то включений кут двох конгруентних сторін першого трикутника більше за мірою, ніж включений кут двох конгруентних сторін другого трикутника.
    Теорема про суму трикутника Теорема про суму трикутника стверджує, що три внутрішні кути будь-якого трикутника складають до 180 градусів.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Порівняння кутів та сторін у принципах трикутників - Основні

    Діяльність: Порівняння кутів і сторін у трикутниках Дискусійні питання

    Навчальні посібники: нерівності в трикутниках Навчальний посібник

    Практика: Порівняння кутів і сторін у трикутниках

    Реальний світ: Теорема про суму трикутника