Skip to main content
LibreTexts - Ukrayinska

4.24: Висоти

  1. Last updated
  2. Save as PDF
  • Page ID
    54903

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Висота трикутника або відрізка лінії від вершини і перпендикулярно протилежній стороні.

    У трикутнику відрізок лінії від вершини і перпендикулярно протилежній стороні називається висотою. Його ще називають висотою трикутника. Червоні лінії внизу - це всі висоти.

    F-д_Б8Д2С9С3Д429А6С41Д6877 ФДДА 931Б6508Ф1Б86Б1Д4А1012Д50ЕБ08+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Коли трикутник - це прямокутний трикутник, висота або висота - це нога. Якщо трикутник тупий, то висота буде за межами трикутника. Якщо трикутник гострий, то висота буде всередині трикутника.

    Що робити, якщо вам дали один або кілька вимірювань кута трикутника? Як би ви визначали, де буде знайдено висоту трикутника?

    Приклад\(\PageIndex{1}\)

    True або false: Висоти тупого трикутника знаходяться всередині трикутника.

    Рішення

    Кожен трикутник має три висоти. Для тупого трикутника принаймні одна з висот буде знаходитися поза трикутником, як показано на малюнку на початку цього перерізу.

    Приклад\(\PageIndex{2}\)

    Намалюйте висоту для показаного трикутника.

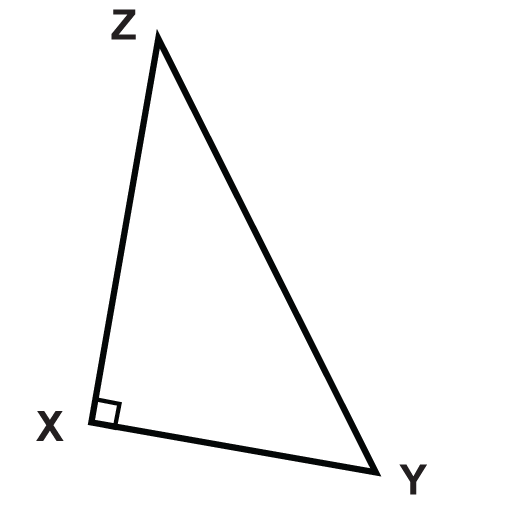
    F-д_Ф 3ДД 9812А401Е27Д7С3Д5Е98Б7988 ФК2А4849ЕЦ73С 8C794102C585+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Трикутник - прямокутний трикутник, тому висота вже намальована. Висота над рівнем моря\(\overline{XZ}\).

    Приклад\(\PageIndex{3}\)

    Який відрізок лінії дорівнює висоті\(\Delta ABC\)?

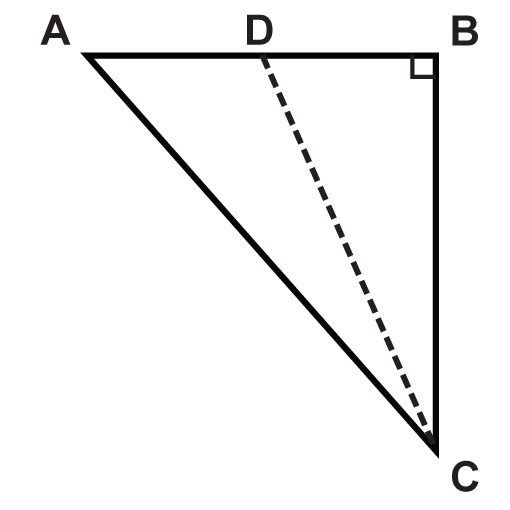
    Ф-Д_9АБ 359Ф131Ф2Ф30902Б71Б6249388Б55ЕЦ939Ф15006274Ф5ДД38C69+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    У прямокутному трикутнику висота, або висота, - це нога. Якщо ми повернемо трикутник так, щоб прямий кут знаходився в лівому нижньому кутку, ми побачимо, що нога\(\overline{BC}\) - це висота.

    Приклад\(\PageIndex{4}\)

    Трикутник має кути, які вимірюють\(55^{\circ}\)\(60^{\circ}\), і\(65^{\circ}\). Де буде знаходитися висота?

    Рішення

    Оскільки всі заходи кута менше\(90^{\circ}\), трикутник - це гострий трикутник. Висота будь-якого гострого трикутника знаходиться всередині трикутника.

    Приклад\(\PageIndex{5}\)

    Трикутник має кут, який вимірює\(95^{\circ}\). Де буде знаходитися висота?

    Рішення

    Тому що\(95^{\circ}>90^{\circ}\), трикутник тупий і він буде за межами трикутника.

    Рецензія

    Враховуючи наступні трикутники, скажіть, чи знаходиться висота всередині трикутника, поза трикутником, або на ніжці трикутника.

    1. F-д_9918д8А 1ББА 78А5648А33966д6Д 6А77Е1Е9334ЕС4С 415ФБ7 Кас 506F8A3B+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{4}\)
    2. F-д_А77362691 ЕФ7Б170935А94932А86ЕА 40А0А6Б1С2739889111СДE0A+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{5}\)
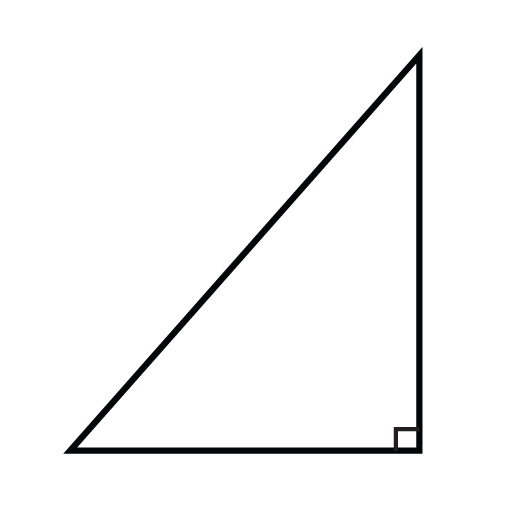
    3. F-д_6 ЕБ7С7Б58Ф12Е79Б4Ф890Е9ДФ098С6Д6КАФ 80333852А98Ф094EC6AE+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{6}\)
    4. F-д_Д8341 ДБ2Б943ДФ3ДФ3Б626БД577С1Д4Ф25Д0Е38А1D983E6B9CD+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
    5. F-д_фафа0Б9Д32АА045 БК 55540 ЕА 1Д161Д58А4875532ЕД 67438ДЕ+зображення_крихіткий+зображення_крихітка_крихітка_png
      Малюнок\(\PageIndex{8}\)
    6. \(\Delta JKL\)являє собою рівнокутний трикутник.
    7. \(\Delta MNO\)являє собою трикутник, в якому два кути вимірюють\(30^{\circ}\) і\(60^{\circ}\).
    8. \(\Delta PQR\)являє собою рівнобедрений трикутник, в якому вимірюються два кути\(25^{\circ}\).
    9. \(\Delta STU\)являє собою рівнобедрений трикутник, в якому вимірюється два кути\(45^{\circ}\).

    З огляду на наступні трикутники, який відрізок лінії є висотою?

    1. \(\Delta ABC \)
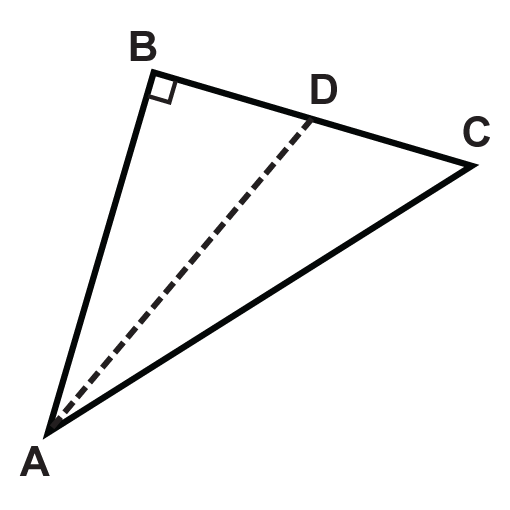
      F-D_01173395 ДАФ 537681Б6461 ФК 985А13 А9 А923А4 А4 БФ 59КД42Б83104+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
    2. \(\Delta EGH \)
      F-D_7D56 АЦП 574187 АЦФ 331Ф4Д3А5Ф22А440ФБ5ДБ5ДБ3ЕФ73АБ542ББ+зображення_крихіткий+зображення_крихіткий.PNG
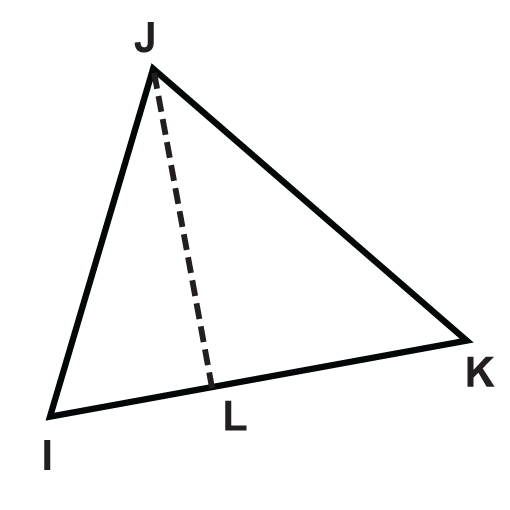
      Малюнок\(\PageIndex{10}\)
    3. \(\Delta IJK \)
      F-д_934943А724905БА982ФБК 261Ф07Ф6Е86ДФ 9715ДФ5334Е90ДФ07ДФА38+зображення_крихіткий+зображення_крихіткий.PNG
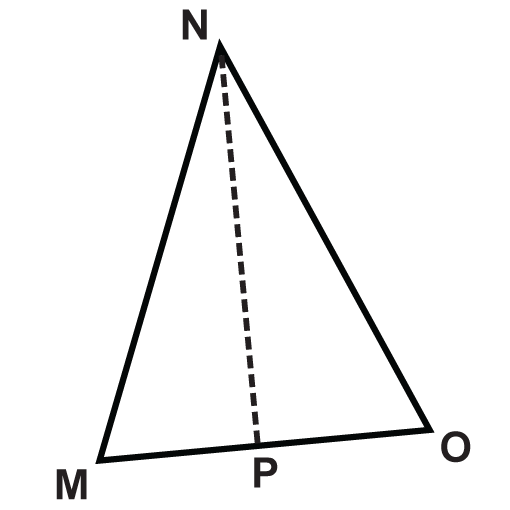
      Малюнок\(\PageIndex{11}\)
    4. \(\Delta MNO \)
      Ф-д_А503Ф6А0БК 06БДС78Д2776Б6Е2189854Д711ААААААС 8Е7929А383Д4Б01+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
    5. \(\Delta RSQ \)
      F-D_A8ABA 805А52179831А105АААААК 0Б2Д733 Бе 798192051AE3690Ф1658БА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)
    6. \(\Delta UVW \)
      F-D_DA2 CF2D85577B39561442E958 Постійний струм 9147 ЕК 475A0DA61F755DC24+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)

    Ресурси

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.5.

    Лексика

    Термін Визначення
    висота Висота трикутника - це відрізок лінії від вершини і перпендикулярний протилежній стороні. Його ще називають висотою трикутника.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Принципи висот - Основні

    Види діяльності: Питання обговорення висот

    Навчальні посібники: Бісектриси, Медіани, Посібник з вивчення висот

    Реальний світ: Висоти