4.23: Медіани
- Page ID
- 54855
Відрізок лінії, який з'єднує вершину і середину протилежної сторони трикутника.
У трикутнику відрізок лінії, який з'єднує вершину і середину протилежної сторони, називається медіаною.
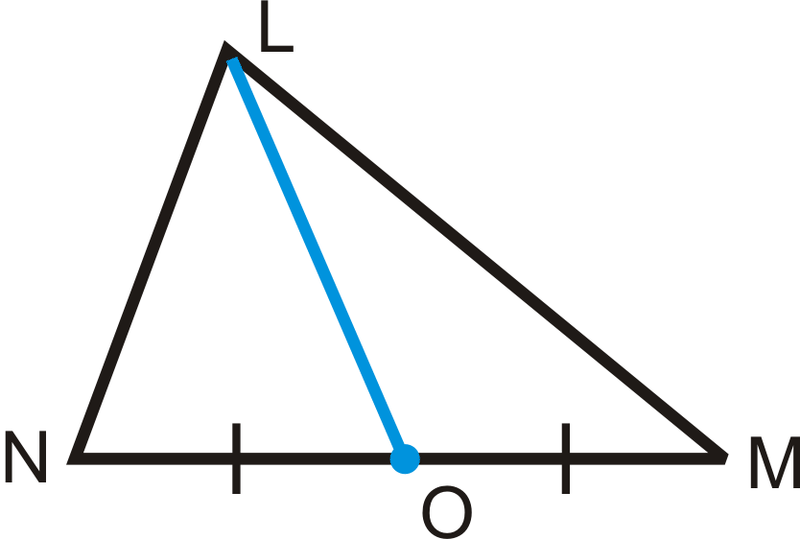
\ overline {LO}\) - медіана від L\) до середини\ overline {NM}\).
Якщо ви намалюєте всі три медіани, вони перетинаються в одній точці, яка називається центроїдом.
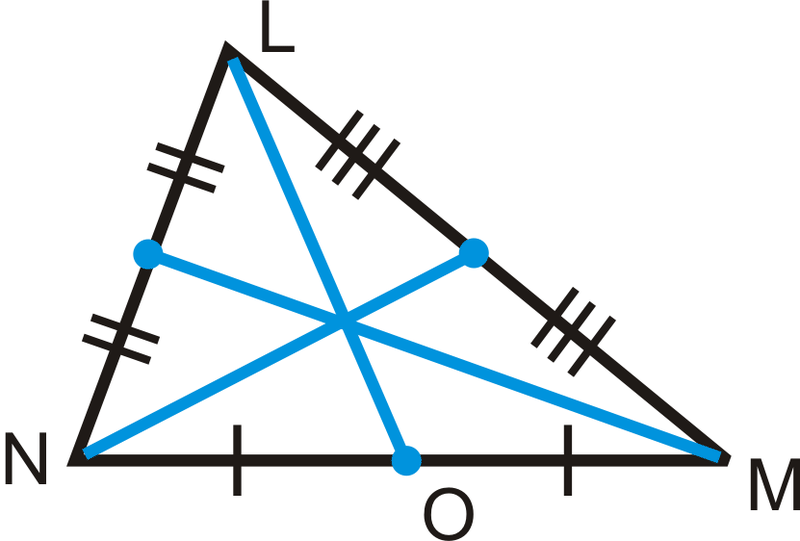
Центроїд - це «точка балансування» трикутника. Це означає, що якщо ви повинні були вирізати трикутник, центроїд є його центром ваги, щоб ви могли врівноважити його там.
Теорема Медіани стверджує, що медіани трикутника перетинаються в точці, яка називається центроїдом, що становить дві третини відстані від вершин до середини протилежних сторін.
Отже\(G\), якщо центроїд, то:
\(AG=\dfrac{2}{3} AD, CG=\dfrac{2}{3} CF,\:EG=\dfrac{2}{3} BE\)
\(DG=\dfrac{1}{3} AD, FG=\dfrac{1}{3} CF,\:BG=\dfrac{1}{3} BE\)
\(And\: by \:substitution:DG =\dfrac{1}{2} AG,\:FG=\dfrac{1}{2} CG,\:BG=\dfrac{1}{2} EG\)
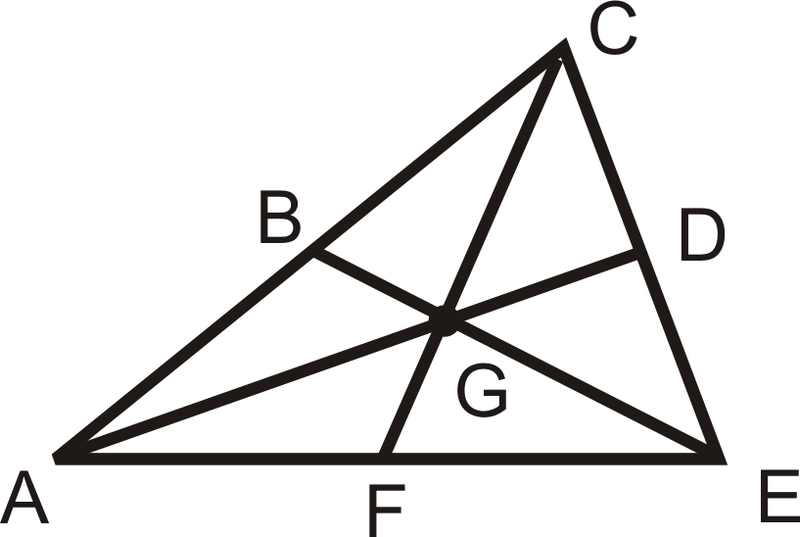
Приклад\(\PageIndex{1}\)
\(B\),\(D\), і\(F\) є серединами кожної сторони і\(G\) є центроїдом. Якщо\(CG=16\), знайдіть\(GF\) і\(CF\).

Рішення
Використовуйте теорему медіани.
\(\begin{align*} CG&=\dfrac{2}{3} CF \\ 16&=\dfrac{2}{3} CF \\ CF&=24.\end{align*}\)
Тому,\(GF=8\).
Приклад\(\PageIndex{2}\)
True або false: Медіана перетинає сторону, яку вона перетинає.
Рішення
Це твердження вірно. За визначенням, медіана перетинає сторону трикутника в його середній точці. Середині розділіть відрізки на дві рівні частини.
Приклад\(\PageIndex{3}\)
\(I\),\(K\), і\(M\) є серединами сторін\(\Delta HJL\).
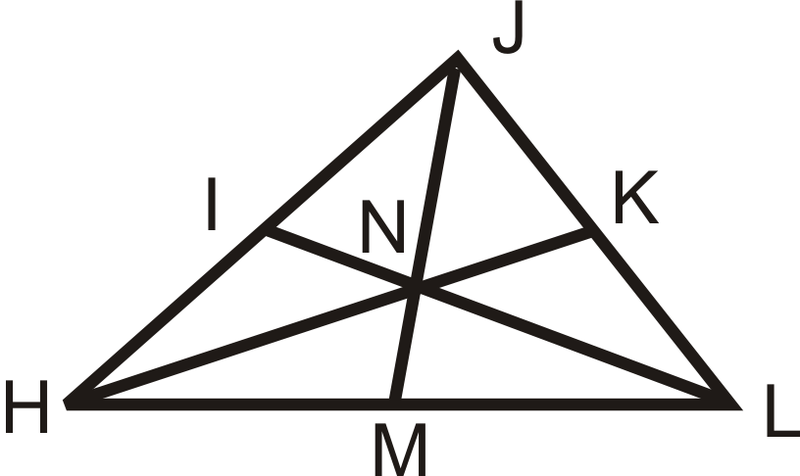
Рішення
Якщо\(JM=18\), знайдіть\(JN\) і\(NM\). Якщо\(HN=14\), знайдіть\(NK\) і\(HK\).
Використовуйте теорему медіани.
\(JN=\dfrac{2}{3} \cdot 18=12. NM=JM−JN=18−12\). \(NM=6\).
\(14=\dfrac{2}{3} \cdot HK\)
\(14\cdot \dfrac{3}{2} =HK=21\). \(NK\)третина з 21,\(NK=7\).
Приклад\(\PageIndex{4}\)
Н - центроїд\(\Delta ABC\) і\(DC=5y−16\). Знайти\(x\) і\(y\).
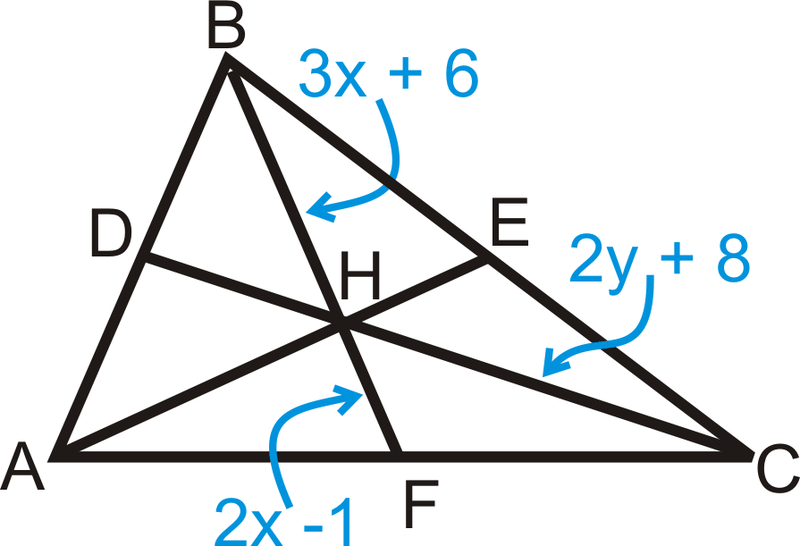
Рішення
Для розв'язання використовуйте теорему Медіани. Налаштуйте та вирішуйте рівняння.
\(\begin{align*} \dfrac{1}{2} BH=HF &\rightarrow BH=2HF &\qquad HC=\dfrac{2}{3} DC &\rightarrow \dfrac{3}{2} HC=DC \\ 3x+6&=2(2x−1) &\qquad \dfrac{3}{2} (2y+8)&=5y−16\\ 3x+6&=4x−2 &\qquad 3y+12 &=5y−16 \\ 8&=x &\qquad 28&=2y\rightarrow 14=y\end{align*} \)
Приклад\(\PageIndex{5}\)
\(B\),\(D\), і\(F\) середні точки кожної сторони, а G - центроїд. Якщо\(BG=5\), знайдіть\(GE\) і\(BE\)

Рішення
Використовуйте теорему медіани.
\(\begin{align*} BG&=\dfrac{1}{3} BE \\ 5&=\dfrac{1}{3} BE \\ BE&=15.\end{align*}\)
Тому,\(GE=10\).
Рецензія
Для питань 1-4\(B\),\(D\),, і\(F\) є серединами кожної сторони і\(G\) є центроїдом. Знайдіть наступні довжини.

- Якщо\(CG=16\), знайдіть\(GF\) і\(CF\)
- Якщо\(AD=30\), знайдіть\(AG\) і\(GD\)
- Якщо\(GF=x\), знайдіть\(GC\) і\(CF\)
- Якщо\(AG=9x\) і\(GD=5x−1\), знайдіть\(x\) і\(AD\).
Багатоступінчасті задачі Знайти рівняння медіани в площині x−y\).
- Ділянка\(\Delta ABC:\:A(−6,4)\),\ :B (−2,4)\)\ :і\ :C (6, −4)\)
- Знайдіть середню точку\(\overline{AC}\). Позначте його\(D\).
- Знайдіть ухил\(\overline{BD}\).
- Знайдіть рівняння\(\overline{BD}\).
- Ділянка\(\Delta DEF:\: D(−1,5),\:E(1,0),\:F(6,3)\)
- Знайдіть середню точку\(\overline{EF}\). Позначте його\(G\).
- Знайдіть ухил\(\overline{DG}\).
- Знайдіть рівняння\\(overline{DG}\).
Визначте, чи є таке твердження істинним чи хибним.
- Центроїд - це точка балансування трикутника.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.4.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| центроїд | Центроїд - це точка перетину медіан в трикутнику. |
| Медіана | Медіана трикутника - це відрізок лінії, який з'єднує вершину з середньою точкою протилежної сторони. |
Додаткові ресурси
Інтерактивний елемент
Відео: Медіани трикутника
Види діяльності: Медіан Дискусійні питання
Навчальні посібники: Бісектриси, Медіани, Посібник з вивчення висот
Реальний світ: Медіани