Skip to main content
LibreTexts - Ukrayinska

4.22: Конкурс і конструкції

  1. Last updated
  2. Save as PDF
  • Page ID
    54830

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Конструкції, пов'язані з теоремами, що включають окружні центри та інші точки перетину трьох і більше ліній.

    З огляду на трикутник, яка різниця між вписаним колом трикутника та описаним кругом трикутника?

    Вписані та описані кола трикутників

    Враховуючи трикутник, вписане коло є найбільшим колом, що міститься в трикутнику. Вписане коло буде стосуватися кожної з трьох сторін трикутника рівно в одній точці. Центр кола, вписаного в трикутник, - це вцентр трикутника, точка, де зустрічаються бісектриси кута трикутника.

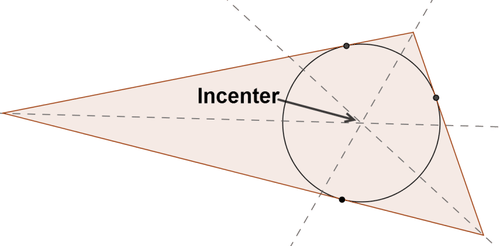
    F-D_4148698b03cd34c45868C2874 ABF 498417CA16797696A64C811BA85B+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{1}\)

    Для побудови вписаного кола:

    1. Побудуйте інцентр.
    2. Побудуйте лінію, перпендикулярну одній стороні трикутника, яка проходить через центр. Відрізок, що з'єднує інцентр з точкою перетину трикутника і перпендикулярною лінією, є радіусом кола.
    3. Побудуйте коло з центром у центрі з радіусом, знайденим на кроці 2.
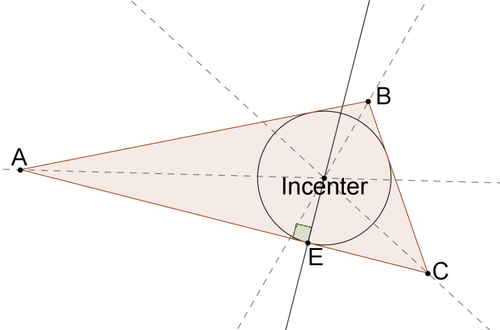
    F-D_D9E1BFC7C FABF CAFC 40F34536282D8B3C1FADA897DB14CFC3BFB1746+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{2}\)

    Етапи побудови вписаного кола для даного трикутника будуть досліджені в задачах нижче.

    Задано трикутник, описане коло - це коло, яке проходить через всі три вершини трикутника. Центр описуваної окружності - це окружний центр трикутника, точка, де зустрічаються перпендикулярні бісектриси сторін.

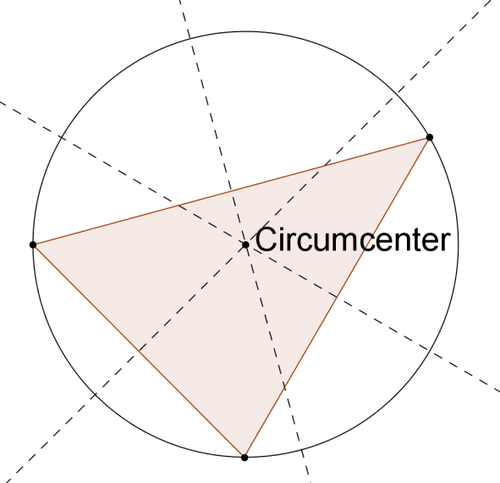
    F-D_10f40d66c5699CA591755F0C0956a7205DD81AA9EE85AED80b9B309A+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{3}\)

    Для побудови описаного кола:

    1. Побудуйте центр окружності.
    2. Побудувати коло по центру окружності, що проходить через одну з вершин. Цей же коло повинен проходити через всі три вершини.

    Етапи побудови описаного кола для заданого трикутника будуть розглянуті в розділі Приклади.

    Побудова кутових бісектрис

    Намалюйте трикутник. Побудувати бісектриси кута двох його кутів. Чому точка перетину двох кутових бісектрис є інцентром кола?

    Використовуйте компас і straightedge, щоб побудувати бісектрису кута одного з кутів.

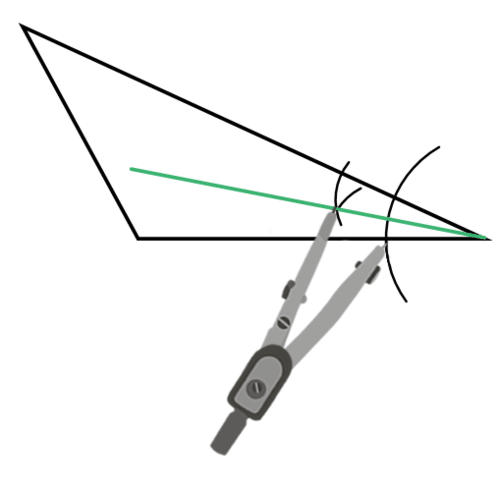
    F-D_E0810E99168C066106987E73117352599A4D195073BFF6A35BBDF16+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{4}\)

    Повторіть з другим кутом.

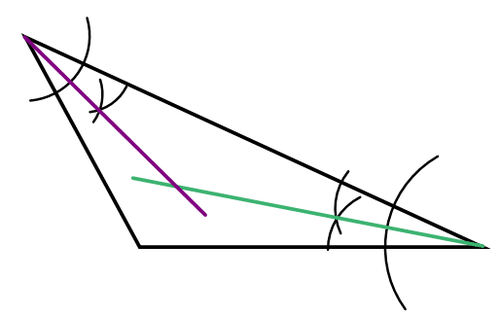
    F-D_AF2A804899145984322AAD335710DE444ADBC03C1032198E14F375F8+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{5}\)

    Точка перетину бісектрис кута - це інцентр. Не потрібно будувати всі три кутові бісектриси, оскільки всі вони зустрічаються в одній точці. Третя бісектриса кута не дає жодної нової інформації.

    Побудова перпендикулярних ліній

    Побудуйте лінію, перпендикулярну одній стороні трикутника, яка проходить через центр трикутника.

    Використовуйте компас і straightedge, щоб побудувати лінію, перпендикулярну одній стороні трикутника, яка проходить через центр.

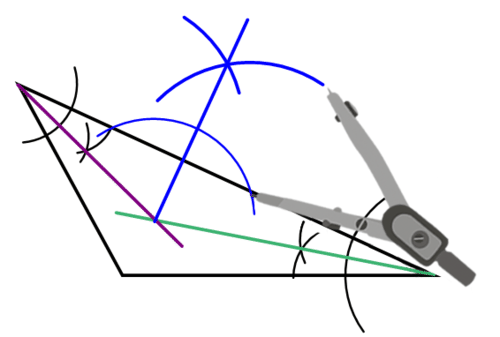
    F-D_8D10f978B767F61979 EDB26F1AAAD3DE16A58164292116A087E13557+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{6}\)

    Побудова вписаних кіл

    Побудуйте коло з центром у центрі, яке проходить через точку перетину сторони трикутника і перпендикулярної лінії від задачі вище.

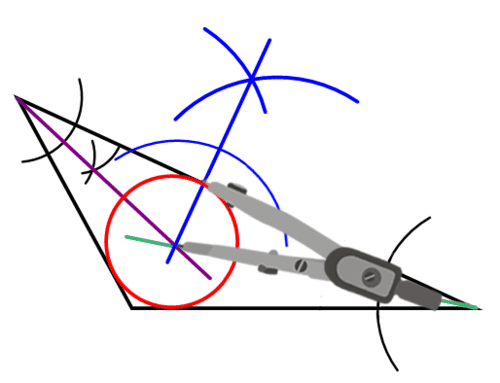
    F-D_1С2Б5Б61Б61E66C587784E4A64B5C3129EF6D70368F07F07E6+зображення_thumb_поштова листівка_крихіткий+зображення_thumb_поштова листівка_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Зверніть увагу, що це коло стосується кожної сторони трикутника рівно один раз.

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, в чому різниця між вписаною окружністю трикутника і описаної окружністю трикутника.

    Рішення

    Вписана окружність трикутника знаходиться всередині трикутника. Описується коло трикутника знаходиться поза трикутником.

    Приклад\(\PageIndex{2}\)

    Намалюйте трикутник. Побудувати перпендикулярні бісектриси двох його сторін. Чому точка перетину двох перпендикулярних бісектрис є центром окружності?

    Рішення

    Використовуйте компас і straightedge, щоб побудувати перпендикулярну бісектрису однієї сторони.

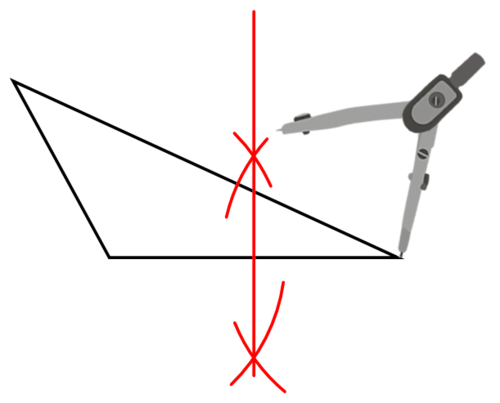
    F-D_78D782A11760132464CF29F7C2910a8C4012263435c690F4BDC0EC9C+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{8}\)

    Повторіть з другою стороною.

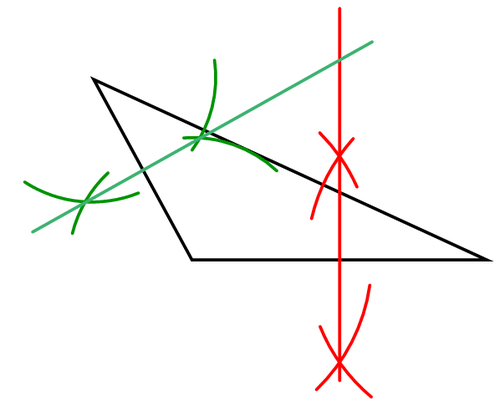
    F-D_9A5C5E20BA96097975E53414980DCC280d5186db9EE178588BD2227E+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_png
    Малюнок\(\PageIndex{9}\)

    Точка перетину перпендикулярних бісектрис - циркуцентр. Не потрібно будувати всі три перпендикулярні бісектриси, оскільки всі вони зустрічаються в одній точці. Третя перпендикулярна бісектриса не дає жодної нової інформації.

    Приклад\(\PageIndex{3}\)

    Продовжуйте з трикутником з #2. Побудувати описану окружність трикутника.

    Рішення

    Побудувати коло по центру окружності, що проходить через одну з вершин трикутника. Ця окружність повинна проходити через всі три вершини.

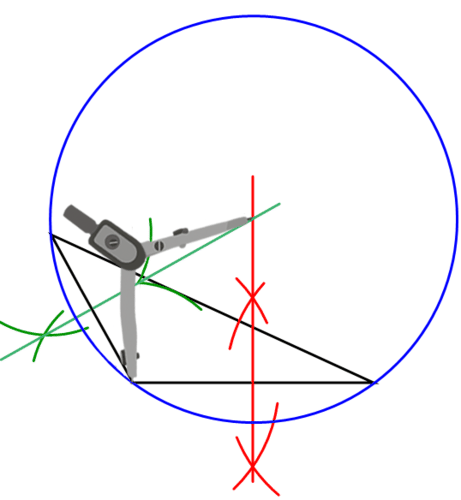
    F-D_142b345f10ee1af039efc fbddde3af134065b86139064c364015DE1+зображення_thumb_поштова листівка_крихітка+зображення_thumb_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{10}\)

    Приклад\(\PageIndex{4}\)

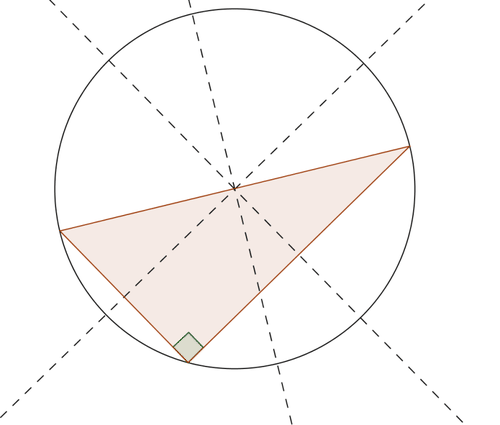
    Обґрунтуйте твердження: гіпотенузою прямокутного трикутника буде діаметром описаної окружності трикутника.

    Рішення

    Кожен з кутів, що складають трикутник, стають вписаними кутами описаного кола. \(90^{\circ}\)Кут буде перехоплювати дугу\(180^{\circ}\), яка становить половину кола. Тому сторона, протилежна\(90^{\circ}\) куту трикутника, повинна бути діаметром кола.

    F-D_3091181696FC9DD2096F6ABE7C4F078C8B598ec4EF2639F72b58CB1+зображення_thumb_поштова листівка_крихітка+зображення_великий палецька_листівка_крихітка_png
    Малюнок\(\PageIndex{11}\)

    Рецензія

    1. Намалюйте трикутник і побудуйте бісектрису кута двох його кутів.

    2. Продовжуйте з трикутником з #1. Побудуйте лінію, перпендикулярну одній стороні трикутника, яка проходить через центр трикутника.

    3. Продовжуйте з трикутником #1 і #2. Побудувати вписане коло трикутника.

    4. Чому не потрібно було будувати бісектрису кута всіх трьох кутів трикутника?

    5. Поясніть, чому інцентр рівновіддалений від кожної зі сторін трикутника.

    6. Намалюйте трикутник і побудуйте перпендикулярну бісектрису двох його сторін.

    7. Продовжуйте з трикутником з #5. Побудувати описану окружність трикутника.

    8. Поясніть, чому центр окружності рівновіддалений від кожної з вершин трикутника.

    Ви працюєте, продаючи їжу з фуд-вантажівки в місцевому парку. Ви хочете розташувати свою вантажівку так, щоб вона була на однаковій відстані від кожного з трьох місць, показаних на карті нижче.

    F-D_A21CE87025FFFCB0C3185049 ЕФ Кабель 7 ЕСЕА А997396121C40A84AEEDB+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{12}\)

    9. Чи є точка інтересу інцентром або циркумцентром?

    10. Знайдіть точку на карті, яка знаходиться на рівновіддаленій від кожної з трьох локацій.

    11. Як ви могли скласти карту в двох місцях, щоб знайти точку, рівновіддалену від кожної з трьох локацій?

    У вашому місті буде побудована нова початкова школа. План полягає в тому, щоб побудувати школу так, щоб вона перебувала на однаковій відстані від кожної з трьох основних доріг, показаних на карті нижче.

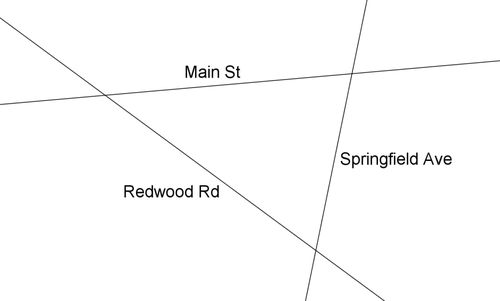
    F-D_FC5E0B350A3D31A5AB24D7ADE135C4CB50365b0FFF35ad03860ed0CD+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png
    Малюнок\(\PageIndex{13}\)

    12. Чи є точка інтересу інцентром або циркумцентром?

    13. Знайдіть на карті точку, яка знаходиться на рівновіддаленій від кожної з трьох доріг.

    14. Як ви могли скласти карту в двох місцях, щоб знайти точку, рівновіддалену від кожної з трьох доріг?

    15. Обґрунтуйте наступне твердження: З урахуванням будь-яких трьох неколінеарних точок існує рівно одне коло, яке проходить через точки.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 8.5.

    Лексика

    Термін Визначення
    перпендикулярна бісектриса Перпендикулярна бісектриса відрізка лінії проходить через середину відрізка лінії і перетинає відрізок лінії в\(90^{\circ}\).
    Вписане коло трикутника Найбільше коло міститься всередині трикутника. Вписане коло буде просто стосуватися кожної з трьох сторін трикутника (вона дотична до кожної з трьох сторін трикутника).

    Додаткові ресурси

    Інтерактивний елемент