Skip to main content
LibreTexts - Ukrayinska

4.21: Кутові бісектриси в трикутниках

  1. Last updated
  2. Save as PDF
  • Page ID
    54872

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Конструкція і властивості бісектрис, які розрізають кути навпіл.

    Теорема про бісектрису кута

    Бісектриса кута розрізає кут рівно навпіл. Однією з важливих властивостей бісектриси кута є те, що якщо точка знаходиться на бісектрисі кута, то точка рівновіддалена від сторін кута. Це називається теоремою бісектриси кута.

    Іншими словами, якщо\(\overrightarrow{BD}\)\(\angle ABC\) розсікає\(\overrightarrow{BA}\perp FD\overline{AB}\), і,\(\overrightarrow{BC}\perp \overline{DG}\) то\(FD=DG\).

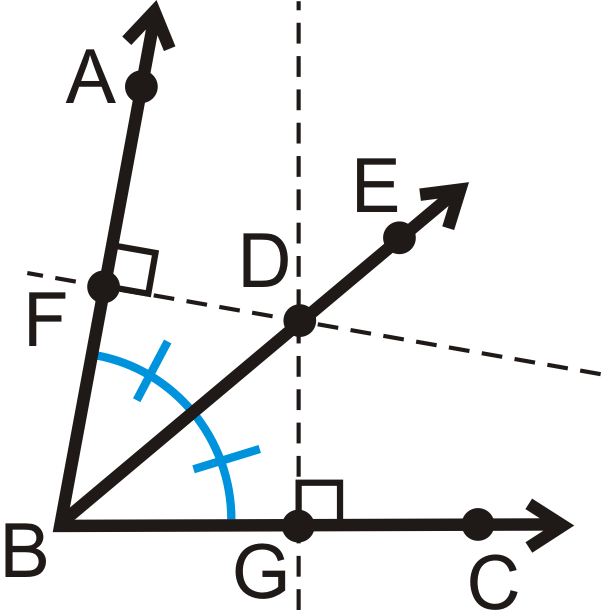
    F-д_889АБ 49 ЕФ394917С87986А6Д 25837924 CE47779961707189D1240906+зображення_крихіткий+зображення_крихіткий_png
    Малюнок\(\PageIndex{1}\)

    Вірно і зворотне значення цієї теореми.

    Теорема бісектриси кута Converse: Якщо точка знаходиться всередині кута і рівновіддалена від сторін, то вона лежить на бісектрисі цього кута.

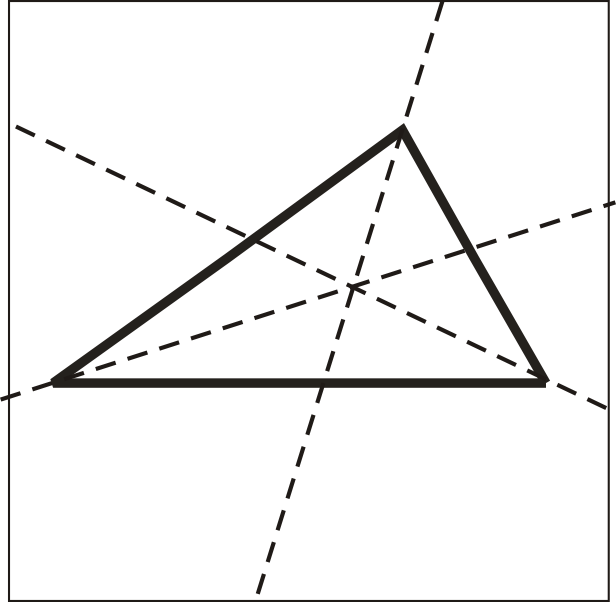
    Коли ми будуємо кутові бісектриси для кутів трикутника, вони зустрічаються в одній точці. Ця точка називається інцентром трикутника.

    F-д_4 ФЕДФ Ф0ББ 605Б65Б4Е1266 АД 46д89 КБД 9975052148Д95Е8Б3Б3 Bee15240+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Що робити, якщо вам сказали, що\(\overrightarrow{GJ}\) це бісектриса кута\(\angle FGH\)? Як би ви знайшли довжину\(FJ\) даної довжини\(HJ\)?

    Приклад\(\PageIndex{1}\)

    Чи достатньо інформації, щоб визначити, чи\(\overrightarrow{AB}\) є кутова бісектриса\(\angle CAD\)? Чому чи чому ні?

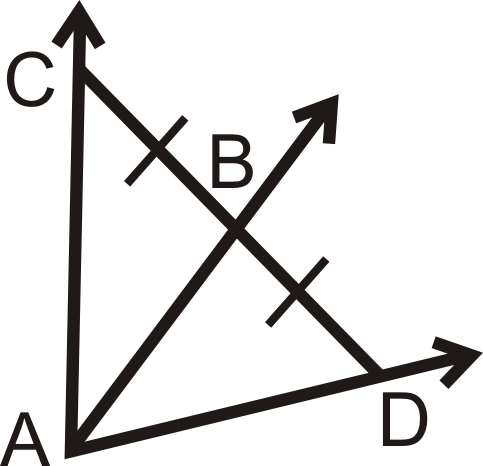
    F-д_д776169A3E60B6E3693852 ББ41Б6А4С30Б5Ф44Е084864Ф2А7D717E+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Рішення

    Ні, тому\(B\) що не обов'язково рівновіддалений від\(\overline{AC}\) і\(\overline{AD}\). Ми не знаємо, чи кути на схемі є прямими кутами.

    Приклад\(\PageIndex{2}\)

    \(108^{\circ}\)Кут розділений навпіл. Які міри одержуваних кутів?

    Рішення

    Ми знаємо, що розрізати навпіл означає розрізати навпіл, тому кожен з отриманих кутів складе половину 108. Міра кожного отриманого кута дорівнює\(54^{\circ}\).

    Приклад\(\PageIndex{3}\)

    Чи є\(Y\) на куті бісектриси\(\angle XWZ\)?

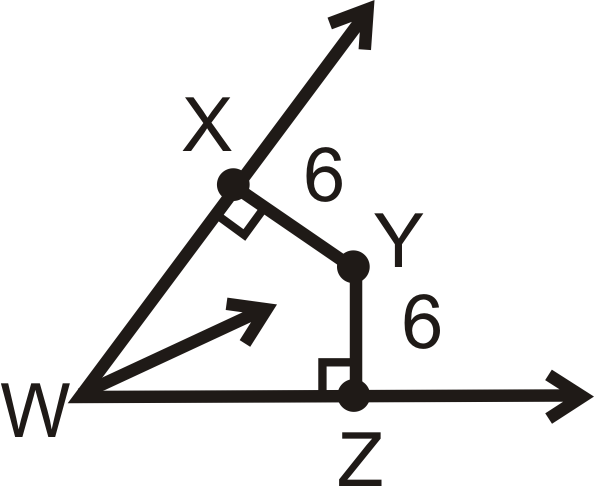
    F-д_22б 6341392E13E4177508 А68Д5Б133828С1377Ф34А4А4Ф900ЕД76А4С+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Якщо\(Y\) на куті бісектриса, то\(XY=YZ\) і обидва відрізки потрібно перпендикулярно сторонам кута. З маркувань ми знаємо\(\overline{XY}\perp \overrightarrow{WX}\) і\(\overline{ZY}\perp \overrightarrow{WZ}\). По-друге,\(XY=YZ=6\). Так, так,\(Y\) знаходиться на куті бісектриси\(\angle XWZ\).

    Приклад\(\PageIndex{4}\)

    \(\overrightarrow{MO}\)є кутом бісектриси\(\angle LMN\). Знайдіть міру\(x\).

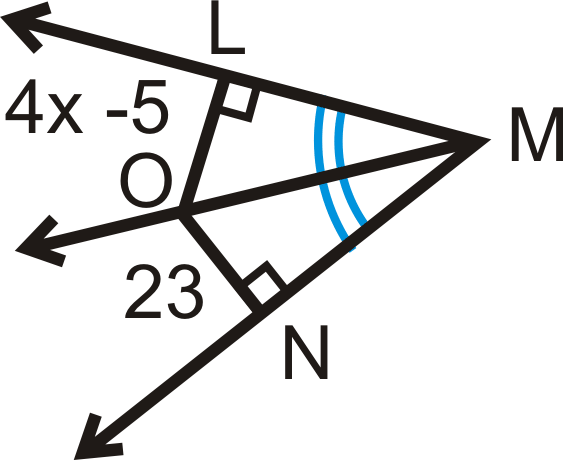
    F-д_04486Ф20ФС 145ЕЕ9ЕБ9824Е3 ЕЕД 9С48880С880С825Б5А83Б1Б4758C7189+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    \(LO=ON\)за теоремою кутової бісектриси.

    \(\begin{align*} 4x−5&=23 \\ 4x&=28 \\ x&=7\end{align*} \)

    Приклад\(\PageIndex{5}\)

    \(\overrightarrow{AB}\)є кутом бісектриси\(\angle CAD\). Вирішити для відсутньої змінної.

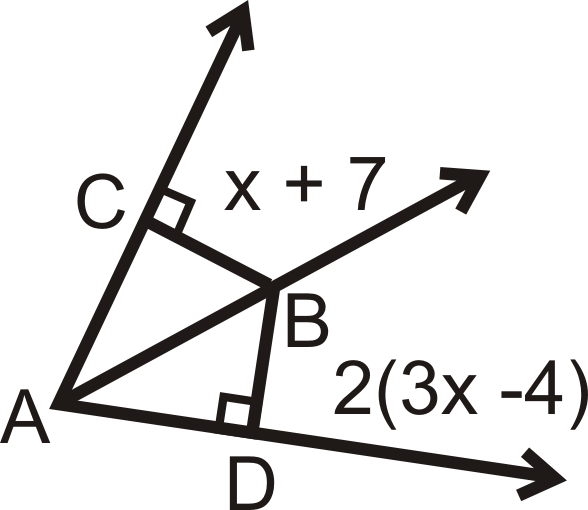
    F-D_A6486 CF6546ABA802FC0D5302814E82DC 9ДБКДЕ4АФД 936306441+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    \(CB=BD\)за теоремою бісектриси кута, так що ми можемо встановити і вирішити рівняння для\(x\).

    \(\begin{align*} x+7&=2(3x−4) \\ x+7&=6x−8 \\ 15x&=5 \\ x&=3\end{align*}\)

    Рецензія

    Для питань 1-4\(\overrightarrow{AB}\) - це кут бісектриси\(\angle CAD\). Вирішити для відсутньої змінної.

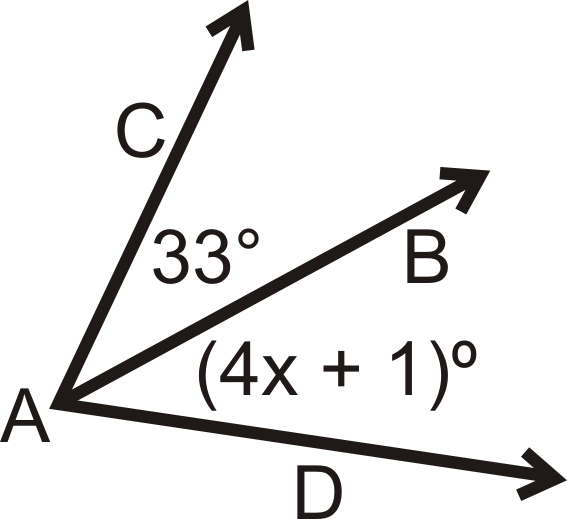
    1. F-D_7ФД8А 0Ф 8384228Д91С3БД 3С354387 ДК630CF3A5E66AECFFD05138+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{7}\)
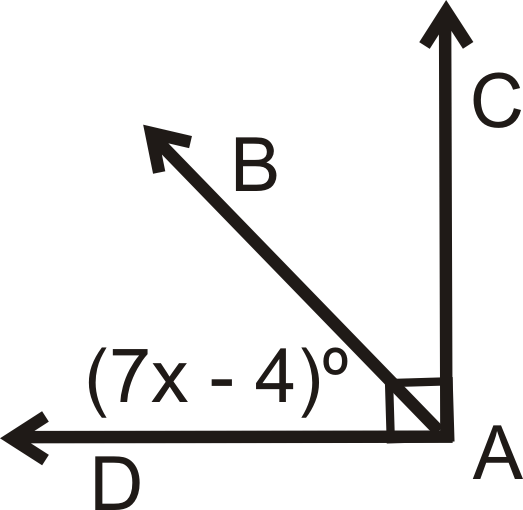
    2. F-д_267939 кд6д9ф46д7Е01Ф309АА07593ЕЕ77КБФ ФКБ4273Б0ФД78+зображення_крихіткий+зображення_крихіткий_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
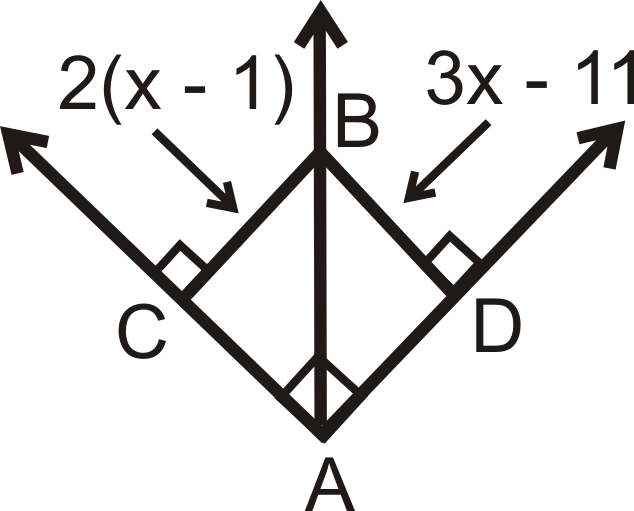
    3. F-д_Е5Ф2Ф 458 БК 5 Ад д 6Ф 679702744c6d8ccc527993A47993A4790517F8A407+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
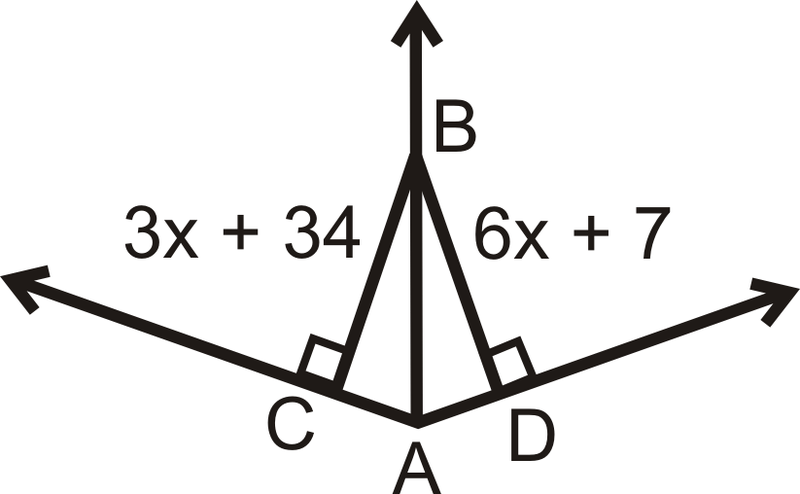
    4. F-D_F8D0DCF74E1485224E2A16D5Д1Б1Е742Д7С8БКС10783 Кабель 4ED5A66+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)

    Чи достатньо інформації, щоб визначити, чи\(\overrightarrow{AB}\) є бісектриса кута\ кута CAD? Чому чи чому ні?

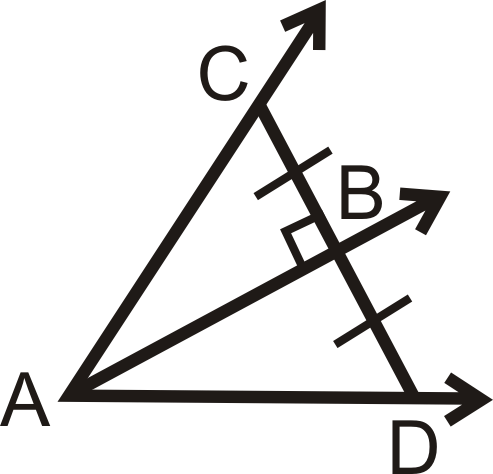
    1. F-D_4E8C638838 БК CA437 Де0Б5Е9 АД Ф 679 АД Ф 5551БФ 15Е6Б0Е331ФА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{11}\)
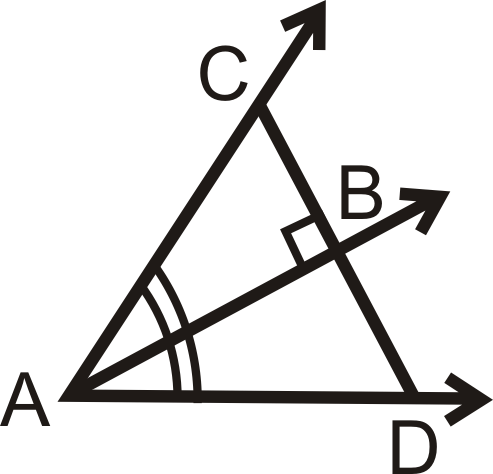
    2. F-D_3DE480A51С4Е0Е0ФББДБ65Б5442Ф074С77Д053ФА4А435Е6ДФ3ДФ3Ф3ДФ33ДФ33ДФ3АА+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{12}\)
    1. У якому типі трикутника всі бісектриси кута будуть проходити через вершини трикутника?
    2. Як інша назва кутових бісектрис вершин квадрата?
    3. Намалюйте в кутових бісектрисах вершин квадрата. Скільки у вас трикутників? Який тип трикутників вони бувають?
    4. Заповніть пробіли в теоремі бісектриси кута Converse.
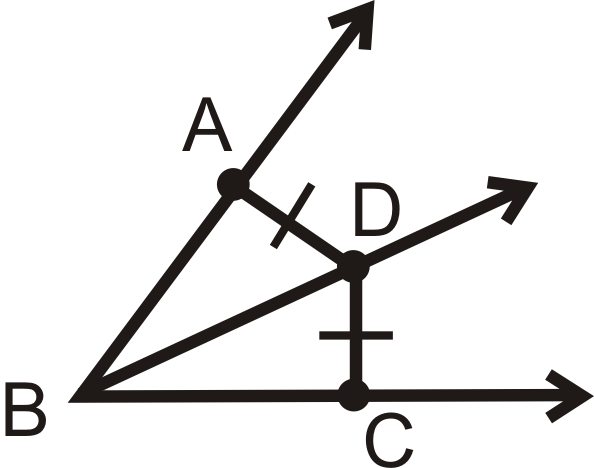
      F-д_ЕД 2358 С987Б9Д8Д2А9307С2С8ФА7А8Ф7Ф71Д52ЕД 328666E8246+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{13}\)

    Дано:\(\overline{AD}\cong \overline{DC}\), такі, що\(AD\) і\(DC\) є найкоротші відстані до\(\overrightarrow{BA}\) і\(\overrightarrow{BC}\)

    Доведіть:\(\overrightarrow{BD} bisects \angle ABC\)

    Заява Причина
    1. 1.
    2. 2. Найкоротша відстань від точки до лінії перпендикулярно.
    3. \(\angle DAB \)і\(\angle DCB\) є прямими кутами 3.
    4. \(\angle DAB\cong \angle DCB\) 4.
    5. \(\overline{BD}\cong \overline{BD}\) 5.
    6. \(\Delta ABD\cong \Delta CBD\) 6.
    7. 7. CPCTC
    8. \(\overrightarrow{BD}\)бісекти\(\angle ABC\) 8.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.3.

    Ресурси

    Лексика

    Термін Визначення
    бісектриса кута Бісектриса кута - це промінь, який розділяє кут на два конгруентні менші кути.
    Теорема про бісектрису кута Теорема бісектриси кута стверджує, що якщо точка знаходиться на бісектрисі кута, то точка рівновіддалена від сторін кута.
    Теорема про бісектрису кута Теорема бісектриси кута converse стверджує, що якщо точка знаходиться всередині кута і рівновіддалена від сторін, то вона лежить на бісектрисі цього кута.
    в центрі Incenter - точка перетину бісектрис кута в трикутнику.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Приклади: Розв'язування невідомих значень з використанням властивостей кутових бісектрис

    Діяльність: Кутові бісектриси в трикутниках Питання обговорення

    Навчальні посібники: Бісектриси, Медіани, Посібник з вивчення висот

    Практика: Кутові бісектриси в трикутниках

    Реальний світ: перпендикулярні бісектриси