4.20: Перпендикулярні бісектриси

Last updated

Oct 27, 2022
Save as PDF
- 4.19: Теорема середнього сегмента
- 4.21: Кутові бісектриси в трикутниках

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Перетинайте відрізки ліній в їх середніх точках і утворюйте з ними кути 90 градусів.

Теорема перпендикулярної бісектриси

Перпендикулярна бісектриса - це лінія, яка перетинає відрізок лінії в середній точці і перпендикулярна цьому відрізку лінії, як показано в конструкції нижче.

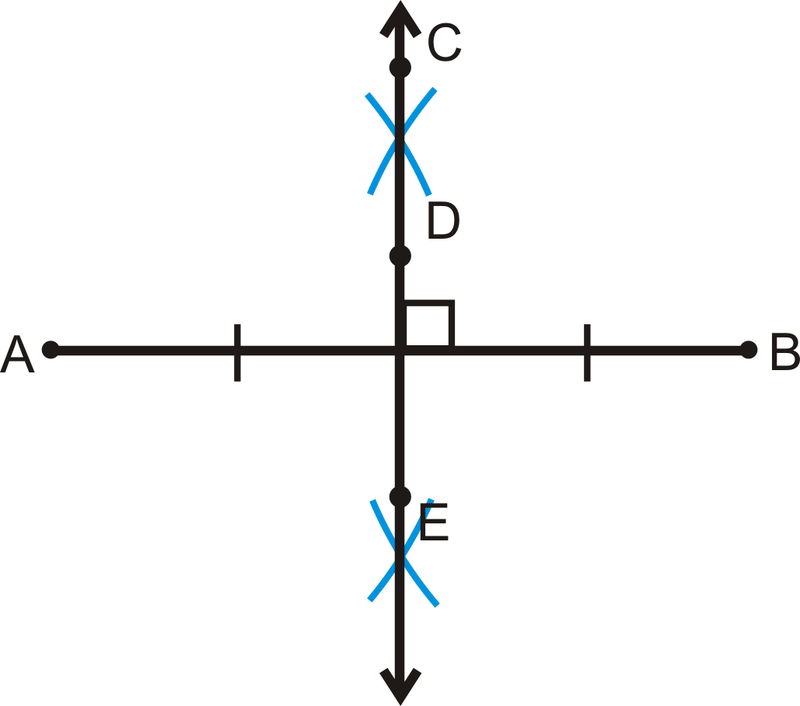
F-D_0054a8 ББД 92Б7Д92С25102801d5f33916c748b55E3A7E469Б417AB7+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Однією з важливих властивостей, пов'язаних з перпендикулярними бісектрисами, є те, що якщо точка знаходиться на перпендикулярній бісектрисі відрізка, то вона рівновіддалена від кінцевих точок відрізка. Це називається теоремою перпендикулярної бісектриси.

Якщо $\overleftrightarrow{CD}\perp \overline{AB}$ і $AD=DB$ , то $AC=CB$ .

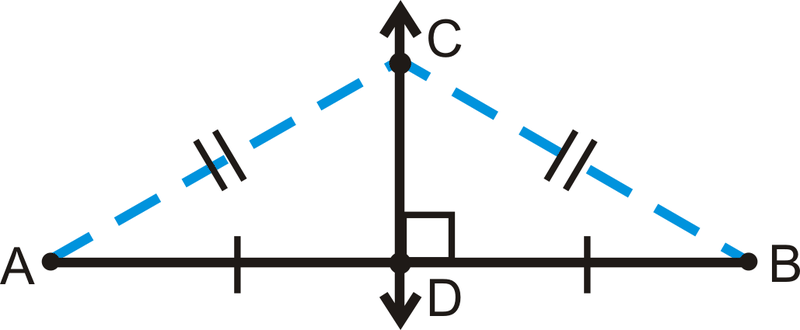
F-д_10068Б965Ф 8675Ф76987Д02А312Д41 Е95Е98043C7E94606FE0+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{2}$

На додаток до теореми перпендикулярної бісектриси, вірно і зворотне.

Перпендикулярна теорема бісектриси Converse: Якщо точка рівновіддалена від кінцевих точок відрізка, то точка знаходиться на перпендикулярній бісектрисі відрізка.

Використовуючи малюнок вище: Якщо $AC=CB$ , то $\overleftrightarrow{CD}\perp \overline{AB}$ і $AD=DB$ .

Коли ми будуємо перпендикулярні бісектриси для сторін трикутника, вони зустрічаються в одній точці. Цю точку називають окружним центром трикутника.

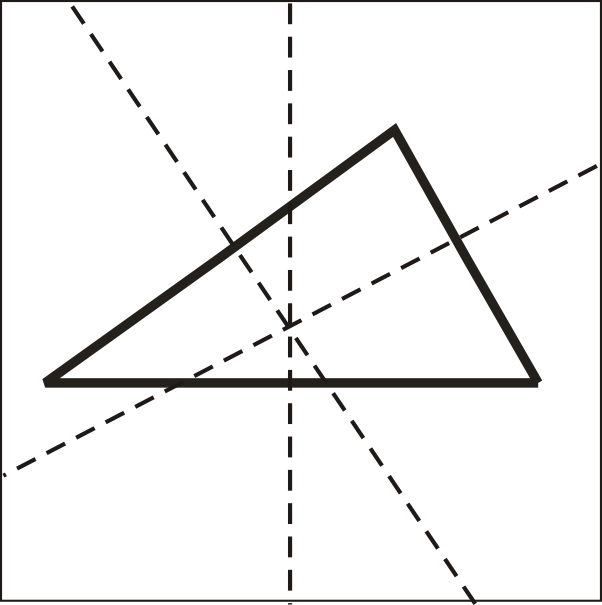
F-д_433867С262А197619126 АА70690А13ЕЕ5С0113Е96Б675ФЕ9Б58+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Що робити, якщо вам дали $\Delta FGH$ і $\overleftrightarrow{GJ}$ сказали, що це перпендикулярна бісектриса $\overline{FH}$ ? Як ви могли знайти довжину FG з урахуванням довжини GH\)?

Приклад $\PageIndex{1}$

$\overleftrightarrow{OQ}$ перпендикулярна бісектриса $\overline{MP}$ .

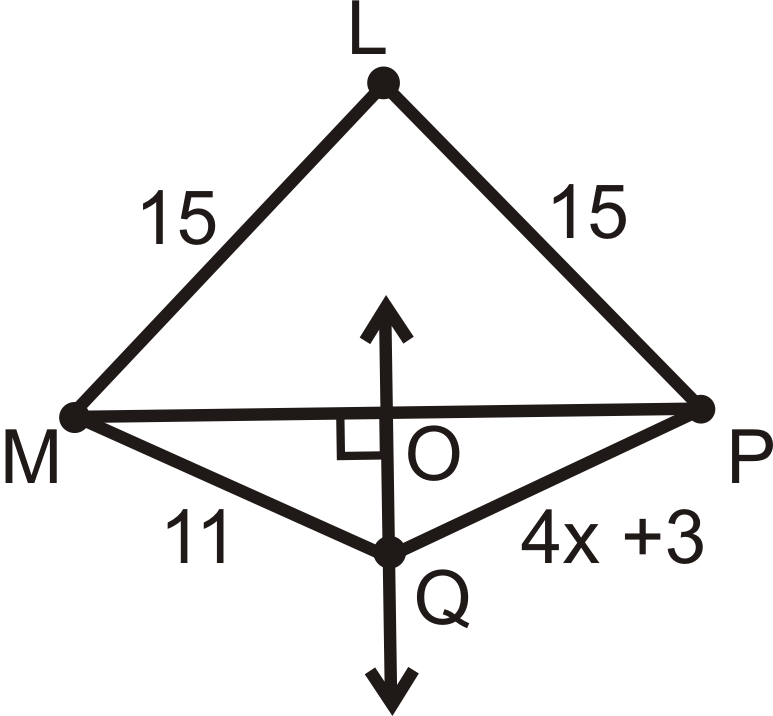
F-д_д140А87Б58FF Додати 3d36edc320117693b93087C6E3ec495201dc7A79+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Які відрізки лінії рівні? Знайти $x$ . $L$ Ввімкнуто $\overleftrightarrow{OQ}$ ? Звідки ти знаєш?

Рішення

$ML=LP$ , $MO=OP$ , і $MQ=QP$ .

$\begin{align*} 4x+3&=11 \\ 4x&=8 \\ x&=2\end{align*}$

Так, $L$ відбувається $\overleftrightarrow{OQ}$ тому, що $ML=LP$ (перпендикулярна теорема бісектриси Converse).

Приклад $\PageIndex{2}$

Визначте $\overleftrightarrow{ST}$ , чи є перпендикулярна бісектриса $\overline{XY}$ . Поясніть, чому чи чому ні.

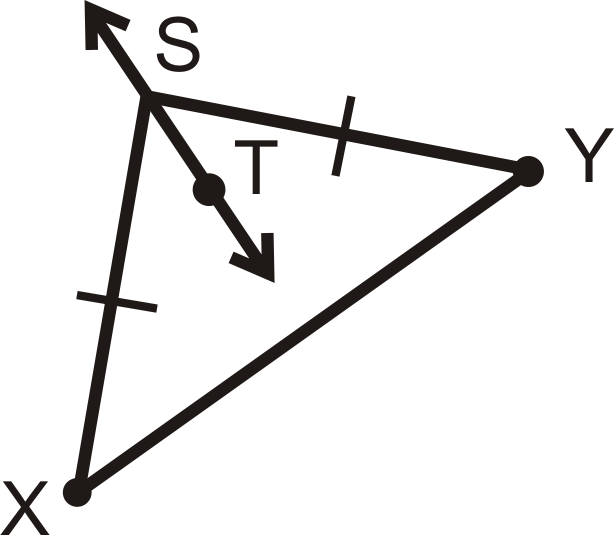
Ф-Д_БА 8КД 1Д238А32Е6042С6684Б025Е2ФЕ8649 CF0561AAF7F0133B2A33+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Рішення

$\overleftrightarrow{ST}$ не обов'язково перпендикулярна бісектриса, $\overline{XY}$ тому що недостатньо інформації наведено на діаграмі. Немає ніякого способу дізнатися з діаграми, якщо $\overleftrightarrow{ST}$ буде розширюватися, щоб зробити прямий кут с $\overline{XY}$ .

Приклад $\PageIndex{3}$

Якщо $\overleftrightarrow{MO}$ − перпендикулярна бісектриса $\overline{LN}$ і $LO=8$ , що таке $ON$ ?

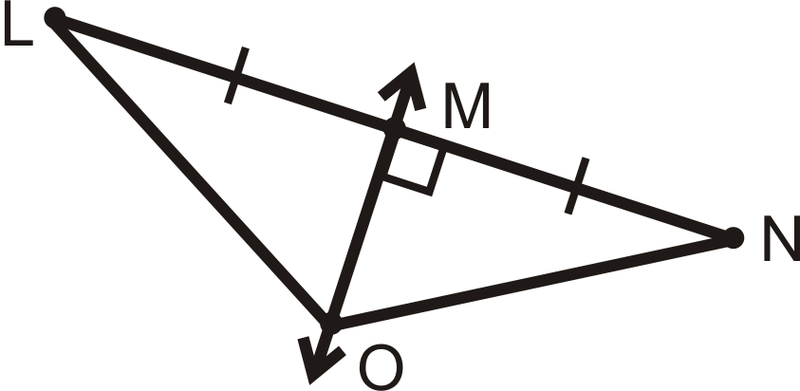
F-D_593C64E8750b5E1 гонорар 95061 фут CC627266b90ddb0EE3d831b2698bfd+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Рішення

За теоремою перпендикулярної бісектриси, $LO=ON$ . Отже, $ON=8$ .

Приклад $\PageIndex{4}$

Знайдіть $x$ і довжину кожного відрізка.

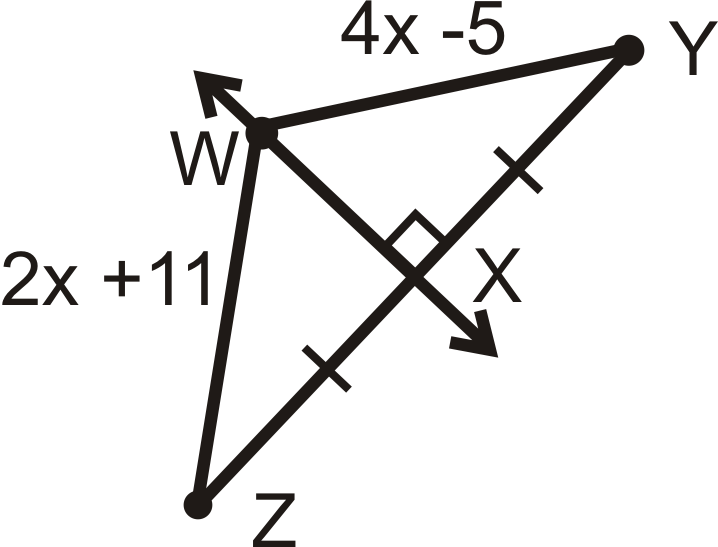
F-д_Д62212БФ 781061578 ЕС8А 3Д 856957327d4d0135362022CC2Фаб64223+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{7}$

Рішення

$\overleftrightarrow{WX}$ − перпендикулярна бісектриса $\overline{XZ}$ та від теореми перпендикулярної бісектриси $WZ=WY$ .

$\begin{align*} 2x+11&=4x−5 \\ 16&=2x \\ 8&=x \end{align*}$

$WZ=WY=2(8)+11=16+11=27$ .

Приклад $\PageIndex{5}$

Знайдіть значення $x$ . $m$ перпендикулярна бісектриса $AB$ .

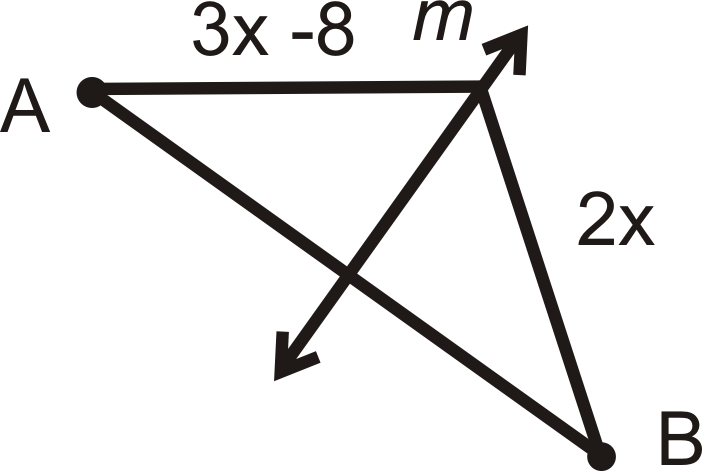
F-D_9C98810069114D983C1CBE4082СБ1А14714Е7АА8БФ739Д7219Е56Ф75+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

Рішення

За теоремою перпендикулярної бісектриси обидва відрізки рівні. Налаштуйте та вирішуйте рівняння.

$\begin{align*}3x−8&=2x \\ x&=8 \end{align*}$

Рецензія

Для питань 1-4 знайти значення $x$ . m\) - перпендикулярна бісектриса $AB$ .

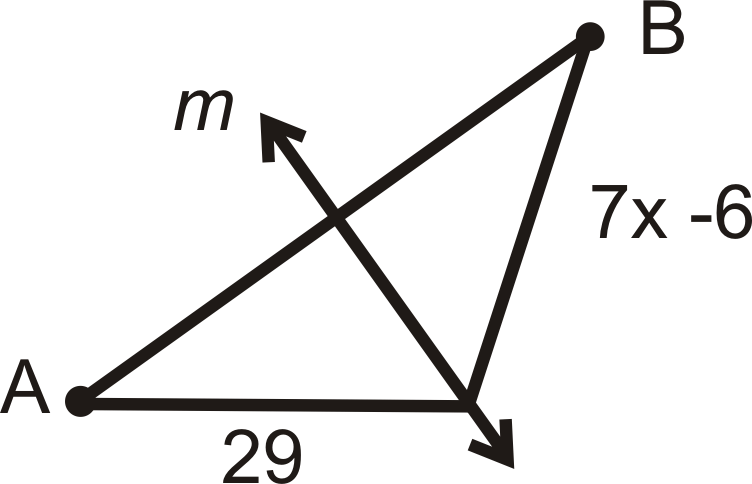
Малюнок $\PageIndex{9}$
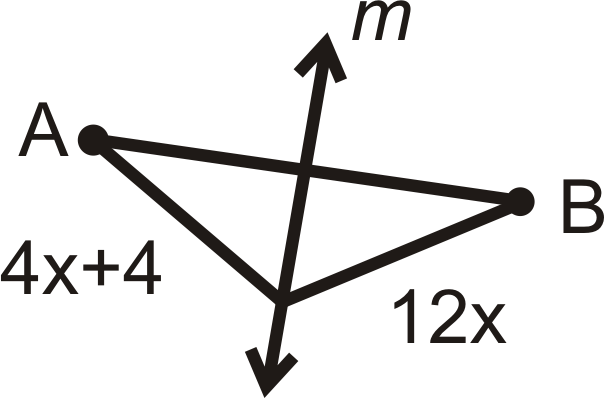
Малюнок $\PageIndex{10}$
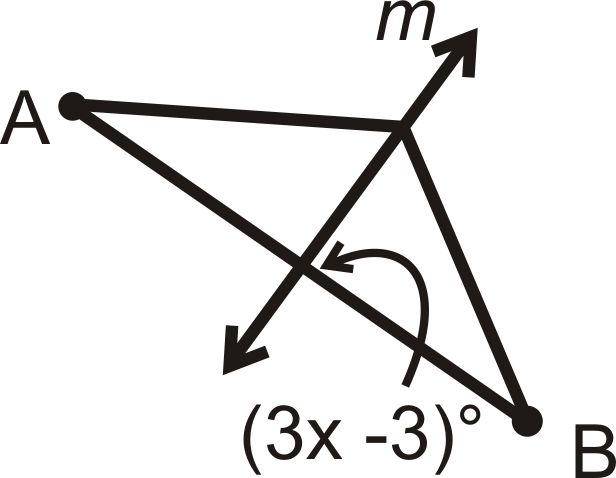
Малюнок $\PageIndex{11}$
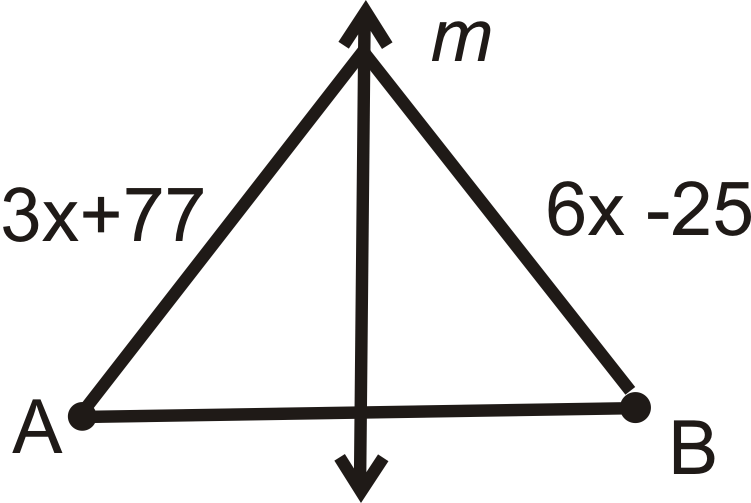
Малюнок $\PageIndex{12}$

m - перпендикулярна бісектриса $\overline{AB}$ .

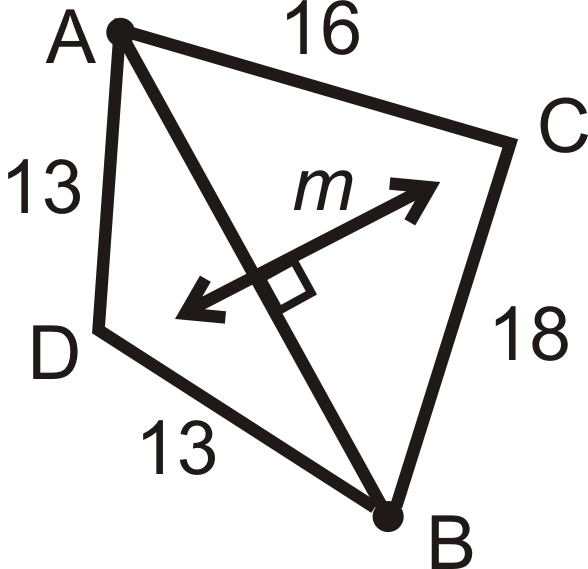
F-д_3Ф4А 69С812А036Д0С50Д4 АБ 9748Е12А9Д25469844716Б4Ф28208264+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{13}$

Перерахуйте всі конгруентні сегменти.
$C$ Ввімкнуто $m$ ? Чому чи чому ні?
$D$ Ввімкнуто $m$ ? Чому чи чому ні?

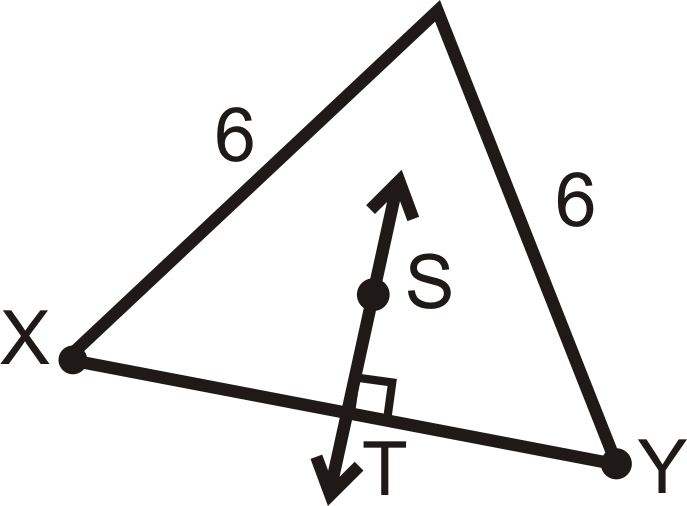
Для питання 8 визначте, чи $\overleftrightarrow{ST}$ є перпендикулярна бісектриса\ overline {XY}\). Поясніть, чому чи чому ні.

$\Індекс сторінки малюнка {14}$
У якому типі трикутника всі перпендикулярні бісектриси будуть проходити через вершини трикутника?
Заповніть пробіли доказу теореми перпендикулярної бісектриси.

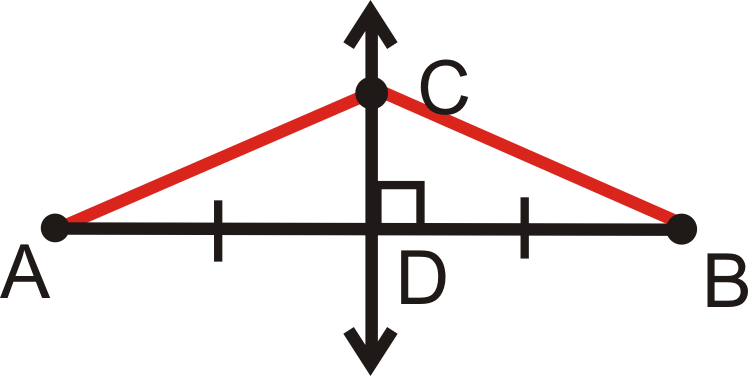
Малюнок $\PageIndex{15}$

Задано: $\overleftrightarrow{CD}$ перпендикулярна бісектриса $\overline{AB}$

Доведіть: $\overline{AC}\cong \overline{CB}$

*Заява*	*Причина*
1.	1.
2. $D$ є середньою точкою $\overline{AB}$	2.
3.	3. Визначення середньої точки
4. $\angle CDA$ і $\angle CDB$ є прямими кутами	4.
5. $\angle CDA\cong \angle CDB$	5.
6.	6. Рефлексивний PoC
7. $\Delta CDA\cong \Delta CDB$	7.
8. $\overline{AC}\cong \overline{CB}$	8.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 5.2.

Лексика

Термін	Визначення
циркумцентр	Окружний центр - точка перетину перпендикулярних бісектрис сторін в трикутнику.
перпендикулярна бісектриса	Перпендикулярна бісектриса відрізка лінії проходить через середину відрізка лінії і перетинає відрізок лінії в $90^{\circ}$ .
Перпендикулярна теорема бісектриси	Якщо точка рівновіддалена від кінцевих точок відрізка, то точка знаходиться на перпендикулярній бісектрисі відрізка.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи перпендикулярної бісектриси - Основні

Діяльність: Перпендикулярні бісектриси Питання обговорення

Навчальна допомога: Бісектриси, Медіани, Посібник з вивчення висот

Практика: Перпендикулярні бісектриси

Реальний світ: перпендикулярні бісектриси