4.19: Теорема середнього сегмента
- Page ID
- 54845
Середній сегмент трикутника з'єднує середні точки двох сторін і становить половину довжини сторони, якій він паралельний.
Відрізок лінії, який з'єднує дві середні точки сторін трикутника, називається середнім сегментом. \(\overline{DF}\)серединний сегмент між\(\overline{AB}\) і\(\overline{BC}\).
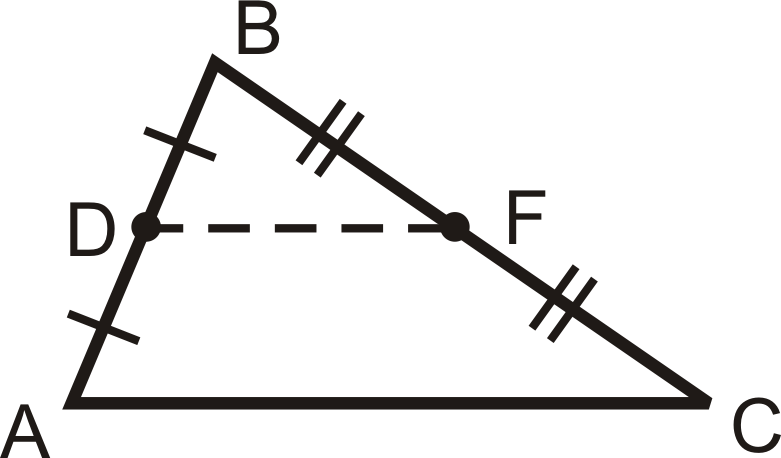
Позначки tic показують, що\(D\) і\(F\) є серединами. \(\overline{AD}\cong \overline{DB}\)і\(\overline{BF}\cong \overline{FC}\). Для кожного трикутника є три серединних сегмента.
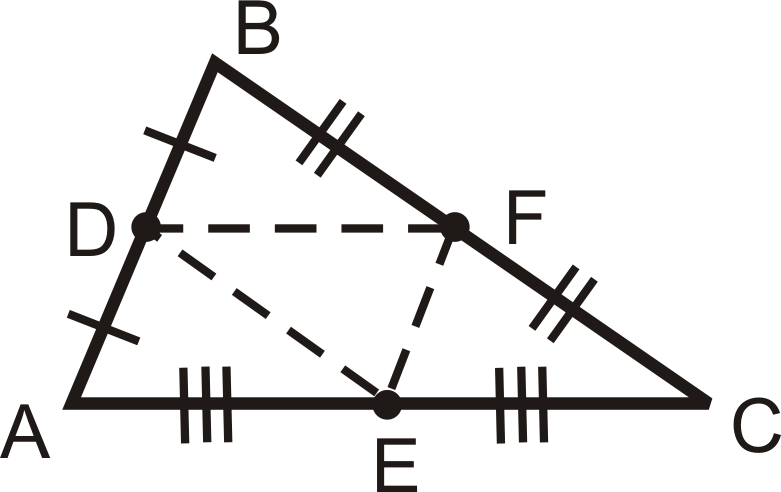
Є дві важливі властивості середніх сегментів, які об'єднуються, щоб зробити теорему середнього сегмента. Теорема середнього сегмента стверджує, що середній сегмент, що з'єднує середні точки двох сторін трикутника, паралельний третій стороні трикутника, а довжина цього середнього сегмента становить половину довжини третьої сторони. Отже, якщо\(\overline{DF}\) є середнім сегментом\(\Delta ABC\), то\(DF=\dfrac{1}{2}AC=AE=EC\) і\(\overline{DF} \parallel \overline{AC}\).
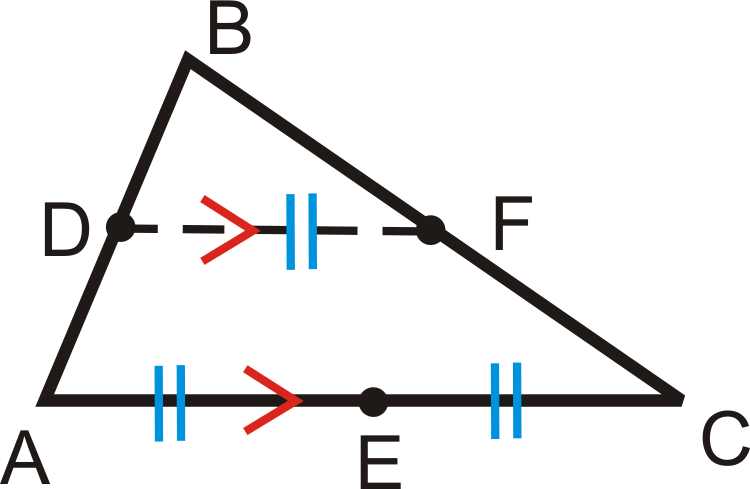
Зверніть увагу, що тут є дві важливі ідеї. Один з них полягає в тому, що середній сегмент паралельний стороні трикутника. Інша полягає в тому, що середній сегмент завжди дорівнює половині довжини цієї сторони.
Що робити, якщо вам дали\(\Delta FGH\) і\(\overline{JK}\) сказали, що це його середній сегмент? Як ви могли знайти довжину\(JK\) заданої довжини третьої сторони трикутника\(FH\)?
Приклад\(\PageIndex{1}\)
Знайдіть значення\(x\) і АВ. \(A\)і\(B\) є серединами.
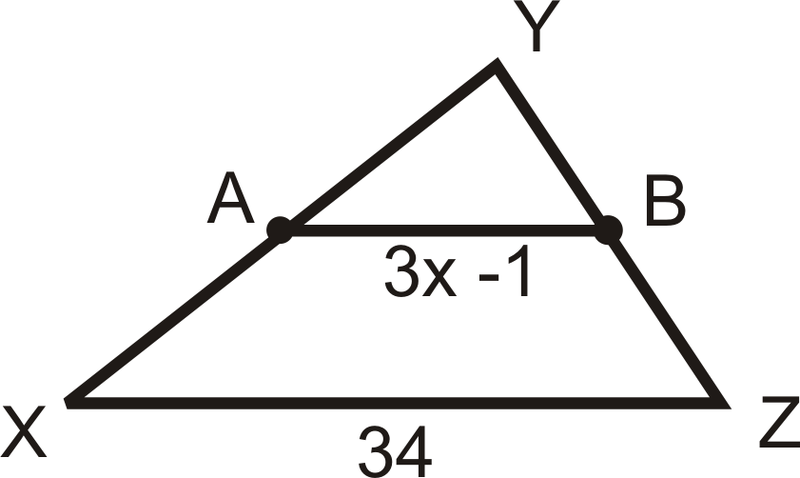
Рішення
\(AB=34\div 2=17\). Щоб знайти\(x\), встановіть\(3x−1\) рівним 17.
\(\begin{align*} 3x−1&=17 \\ 3x&=18 \\ x&=6\end{align*}\)
Приклад\(\PageIndex{2}\)
True або false: Якщо лінія проходить через дві сторони трикутника і паралельна третій стороні, то вона є середнім сегментом.
Рішення
Це твердження є помилковим. Лінія, яка проходить через дві сторони трикутника, є лише середнім сегментом, якщо вона проходить через середні точки двох сторін трикутника.
Приклад\(\PageIndex{3}\)
Вершини\(\Delta LMN\) є\(L(4,5),\: M(−2,−7)\:and\: N(−8,3)\). Знайдіть середні точки всіх трьох сторін, позначте їх O, P і Q. потім намалюйте трикутник, намалюйте середні точки і намалюйте середні сегменти.
Рішення
Щоб вирішити цю проблему, скористайтеся формулою середньої точки 3 рази, щоб знайти всі середні точки. Нагадаємо, що формула середньої точки є\(\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)\).
\(L\)і\(M=\left(\dfrac{4+(−2)}{2}, \dfrac{5+(−7)}{2}\right)=(1,−1),\: point\: O\)
\(M\)і\(N=\left(\dfrac{−2+(−8)}{2},\dfrac{−7+3}{2}\right)=(−5,−2),\: point\: P\)
\(L\)і\(N=\left(\dfrac{4+(−8)}{2}, \dfrac{5+3}{2}\right)=(−2,4),\: point\: Q\)
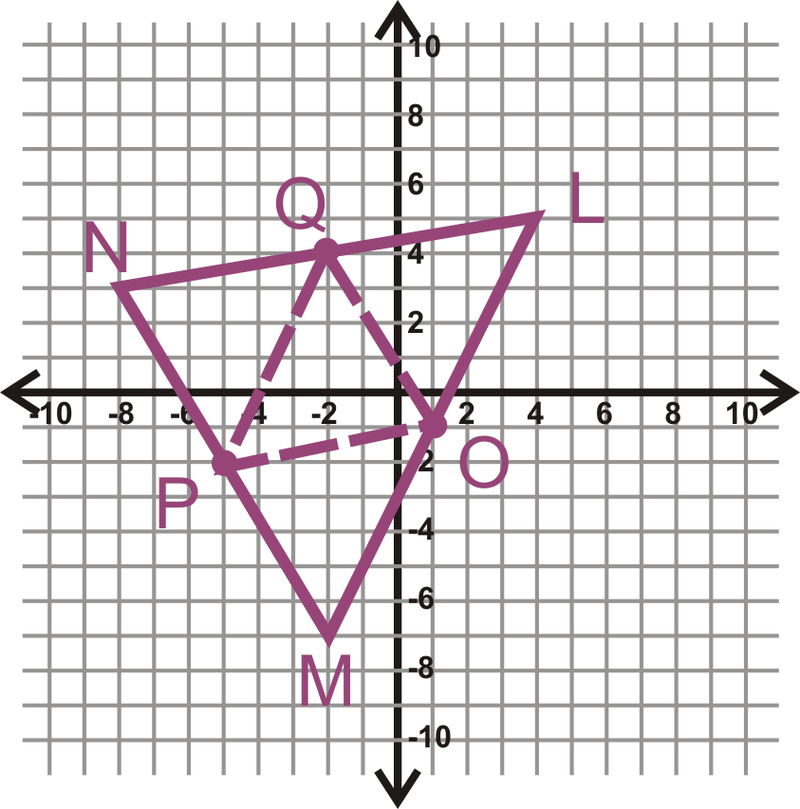
Приклад\(\PageIndex{4}\)

Позначте всі конгруентні сегменти\(\Delta ABC\) з середніми точками\(D\)\(E\), і\(F\).
Рішення
Малюючи у всіх трьох середніх сегментах, ми маємо:
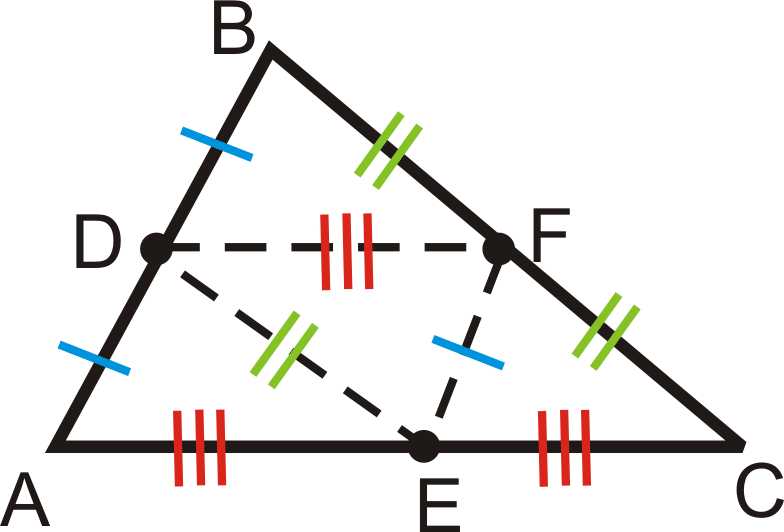
Крім того, це означає, що чотири менші трикутники є конгруентними SSS.
Тепер позначте всі паралельні лінії на\(\Delta ABC\), з серединами\(D\)\(E\), і\(F\).
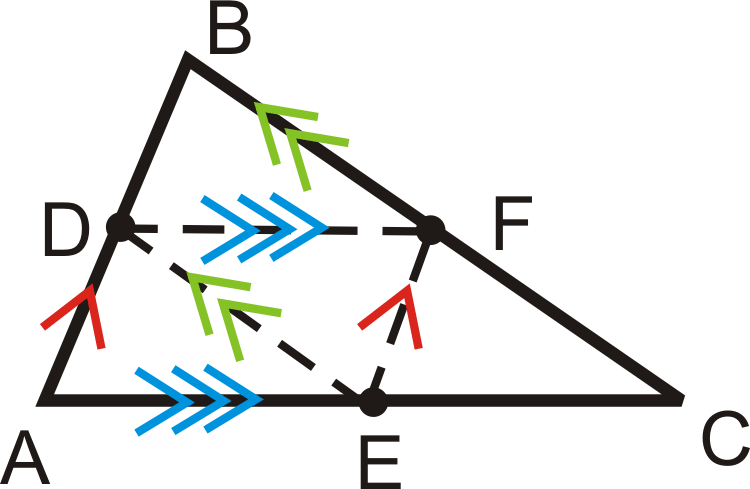
Приклад\(\PageIndex{5}\)
\(M\),\(N\), і\(O\) є серединами сторін\(\Delta \(x\) YZ\).
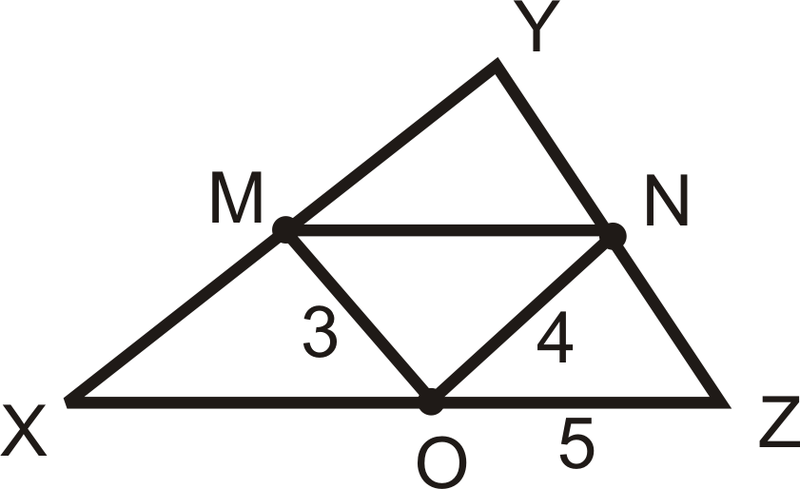
Рішення
Знайти\(MN\)\(XY\), і периметр\(\Delta \(x\) YZ\).
Використовуйте теорему середнього сегмента:
\(MN=OZ=5\)
\(XY=2(ON)=2\cdot 4=8\)
Складіть три сторони,\(\Delta XYZ\) щоб знайти периметр.
\(XY+YZ+XZ=2\cdot 4+2\cdot 3+2\cdot 5=8+6+10=24\)
Пам'ятайте: Відсутність відрізка лінії над MN означає довжину або відстань.
Рецензія
Визначте, чи є кожне твердження істинним чи помилковим.
- Кінцевими точками середнього сегмента є середні точки.
- Середній сегмент паралельний стороні трикутника, щоб він не перетинався.
- Існують три конгруентні трикутники, утворені середніми сегментами та сторонами трикутника.
- У кожному трикутнику є три середні сегменти.
R, S, T і U - середні точки сторін\(\Delta XPO\) і\(\Delta YPO\)
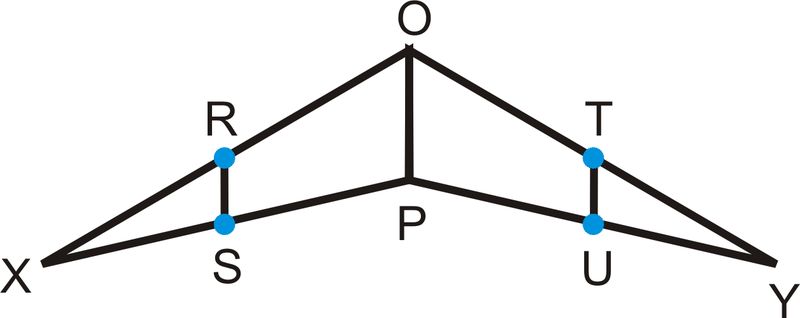
- Якщо\(OP=12\), знайдіть\(RS\) і\(TU\).
- Якщо\(RS=8\), знайдіть\(TU\).
- Якщо\(RS=2x\), і\(OP=20\), знайти\(x\) і\(TU\).
- Якщо\(OP=4x\) і\(RS=6x−8\), знайдіть\(x\).
Для питань 9-15 знайдіть вказану змінну (и). Ви можете припустити, що всі відрізки лінії всередині трикутника є середніми сегментами.
-
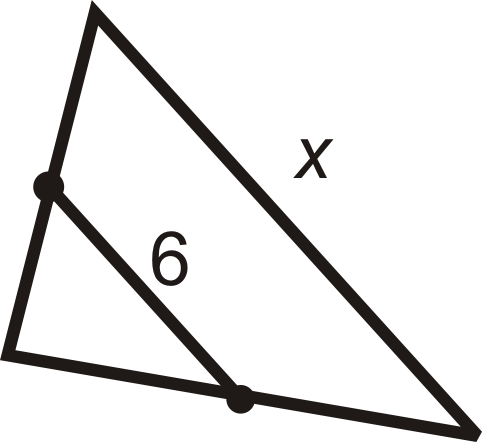
Малюнок\(\PageIndex{11}\) -
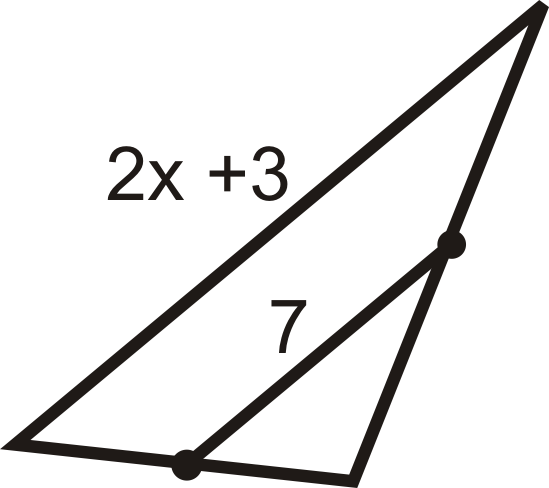
Малюнок\(\PageIndex{12}\) -
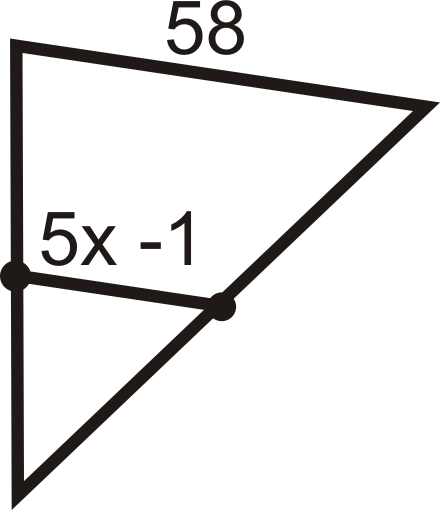
Малюнок\(\PageIndex{13}\) -
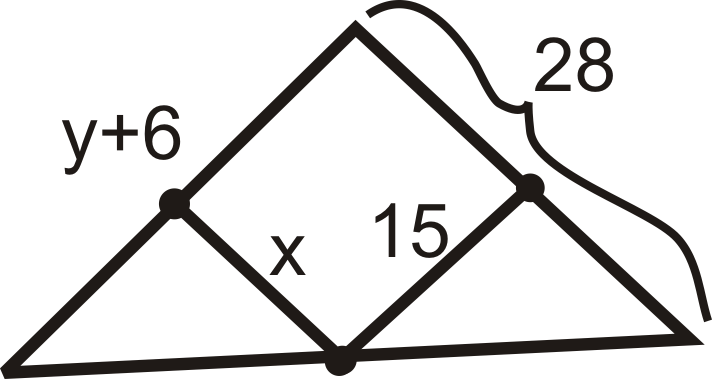
Малюнок\(\PageIndex{14}\) -
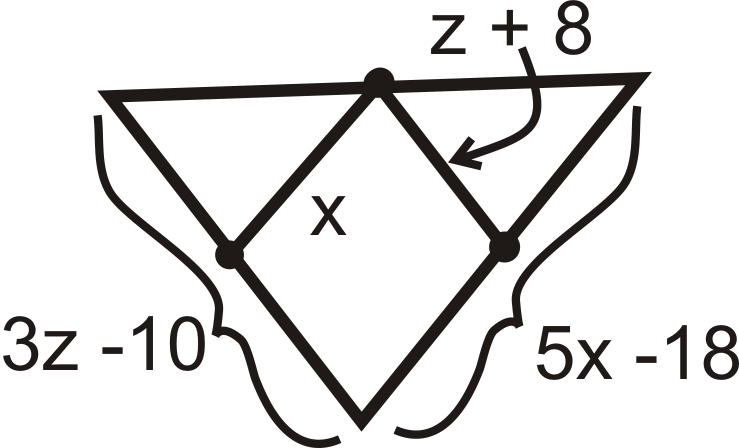
Малюнок\(\PageIndex{15}\) -
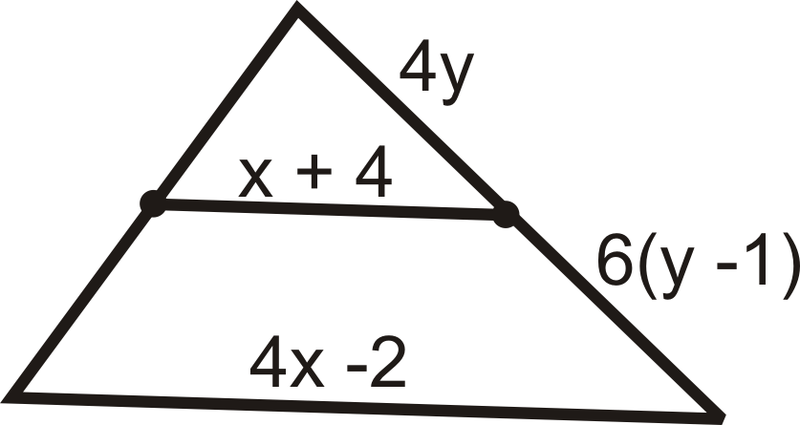
Малюнок\(\PageIndex{16}\) -
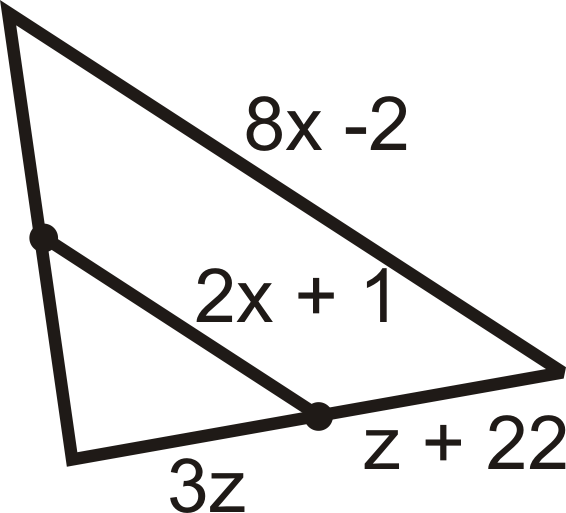
Малюнок\(\PageIndex{17}\) - \(\Delta XYZ\)Сторони - 26, 38 і 42. \(\Delta ABC\)формується шляхом приєднання серединних точок\(\Delta XYZ\).
- Які довжини сторін\(\Delta ABC\)?
- Знайдіть периметр\(\Delta ABC\).
- Знайдіть периметр\(\Delta XYZ\).
- Яка залежність між периметром трикутника і периметром трикутника, утвореного з'єднанням його середніх точок?
Геометрія координат За допомогою вершин\(\Delta ABC\) нижче знайдіть середні точки кожної сторони.
- \(A(5,−2),\: B(9,4)\: and\: C(−3,8)\)
- \(A(−10,1),\: B(4,11)\: and \:C(0,−7)\)
- \(A(−1,3),\: B(5,7)\: and\: C(9,−5)\)
- \(A(−4,−15),\: B(2,−1)\: and\: C(−20,11)\)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.1.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| середній сегмент | Середній сегмент з'єднує середні точки двох сторін трикутника або непаралельних сторін трапеції. |
| Конгруентний | Конгруентні фігури ідентичні за розміром, формою і мірою. |
| Формула середньої точки | Формула середньої точки говорить\((x_2,y_2)\), що для кінцевих точок\((x_1,y_1)\) і середина є (\ dfrac {x_1+x_2} {2},\ frac {y_1+y_2} {2})\). |
Додаткові ресурси
Відео: Визначення невідомих значень за допомогою властивостей середніх сегментів трикутника
Види діяльності: Питання обговорення теореми середнього сегмента
Навчальні посібники: Бісектриси, Медіани, Посібник з вивчення висот
Практика: Теорема середнього сегмента
Реальний світ: теорема середнього сегмента