4.18: Зовнішні кути та теореми
- Page ID
- 54786
Зовнішні кути дорівнюють сумі віддалених інтер'єрів.
Зовнішні кути
Зовнішній кут - це кут, утворений однією стороною багатокутника та продовженням сусідньої сторони.
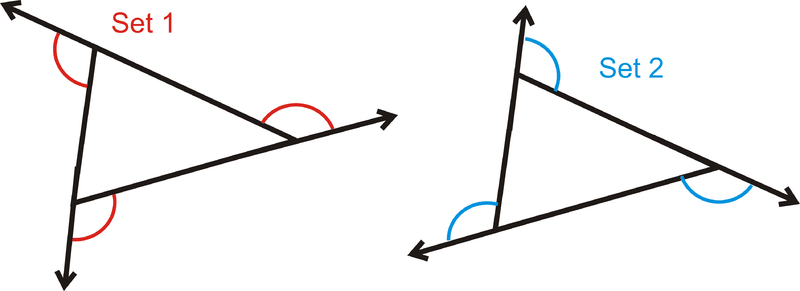
У всіх багатокутників є два набори зовнішніх кутів, один, який йде навколо годинникової стрілки, а інший - проти годинникової стрілки.
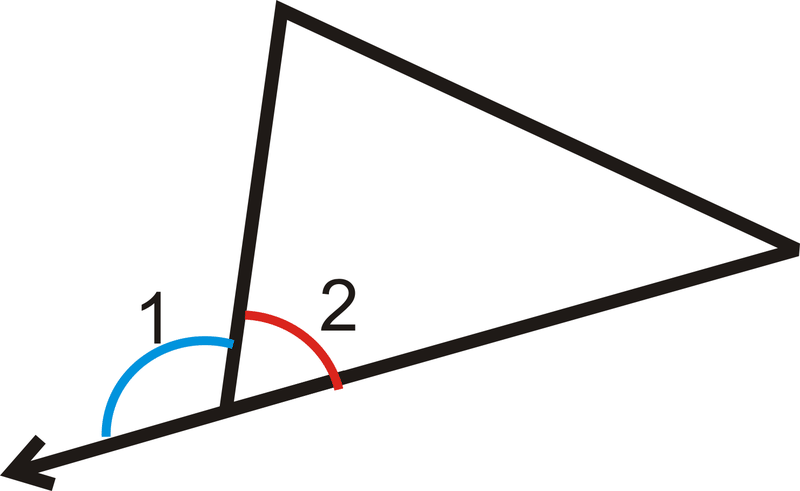
Зверніть увагу, що внутрішній кут і його сусідній зовнішній кут утворюють лінійну пару і складають до\(180^{\circ}\).
\(m\angle 1+m\angle 2=180^{\circ} \)
Є дві важливі теореми, які потрібно знати, що стосуються зовнішніх кутів: Теорема про суму зовнішнього кута та теорема зовнішнього кута.
Теорема про суму зовнішнього кута стверджує, що зовнішні кути будь-якого багатокутника завжди будуть складатися\(360^{\circ}\).
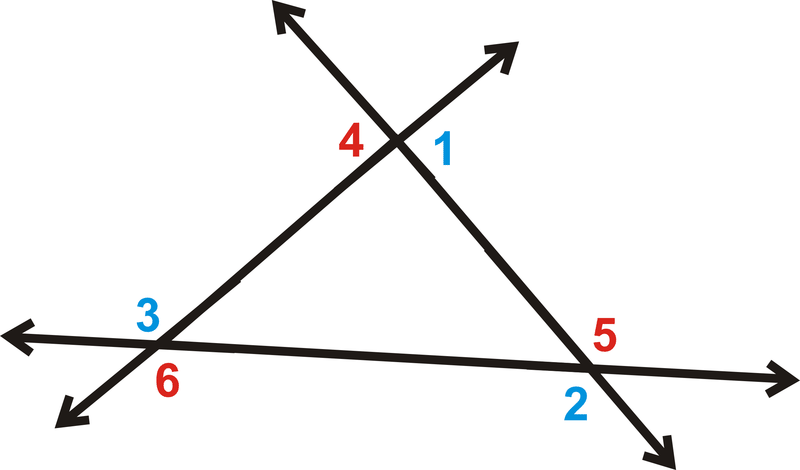
\(m\angle 1+m\angle 2+m\angle 3=360^{\circ}\)
\(m\angle 4+m\angle 5+m\angle 6=360^{\circ}\).
Теорема про зовнішній кут стверджує, що зовнішній кут трикутника дорівнює сумі його віддалених внутрішніх кутів. (Віддалені внутрішні кути - це два внутрішні кути в трикутнику, які не примикають до вказаного зовнішнього кута.)
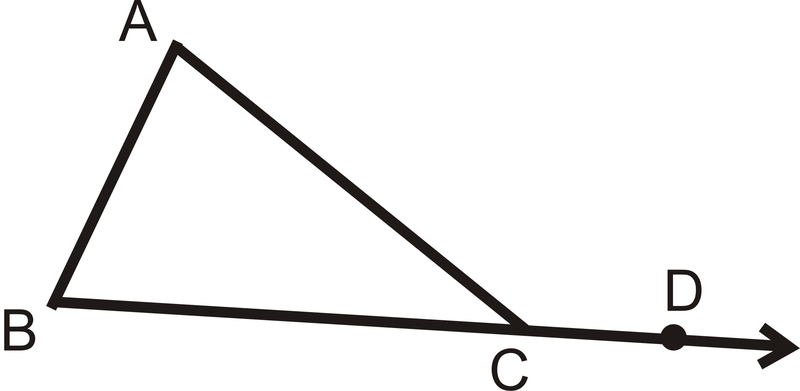Малюнок\(\PageIndex{4}\)\(m\angle A+m\angle B=m\angle ACD\)
Що робити, якби ви знали, що два зовнішніх кути трикутника виміряні\(130^{\circ}\)? Як ви могли знайти міру третього зовнішнього кута?
Приклад\(\PageIndex{1}\)
Два внутрішніх кута трикутника - це\(40^{\circ}\) і\(73^{\circ}\). Які міри трьох зовнішніх кутів трикутника?
Рішення
Пам'ятайте, що кожен внутрішній кут утворює лінійну пару (додає до\(180^{\circ}\)) із зовнішнім кутом. Отже, оскільки один з внутрішніх кутів це означає\(40^{\circ}\), що один із зовнішніх кутів є\(140^{\circ}\) (тому що\(40+140=180\)). Аналогічно, оскільки ще один з внутрішніх кутів є\(73^{\circ}\), один із зовнішніх кутів повинен бути\(107^{\circ}\). Третій внутрішній кут нам не дано, але ми могли б зрозуміти це, використовуючи теорему про суму трикутника. Ми також можемо використовувати теорему про суму зовнішнього кута. Якщо два зовнішніх кути є\(140^{\circ}\) і\(107^{\circ}\), то третій Зовнішній кут повинен бути\(113^{\circ}\) так\(140+107+113=360\).
Так, міри трьох зовнішніх кутів - 140, 107 і 113.
Приклад\(\PageIndex{2}\)
Знайдіть значення\(x\) і міру кожного кута.
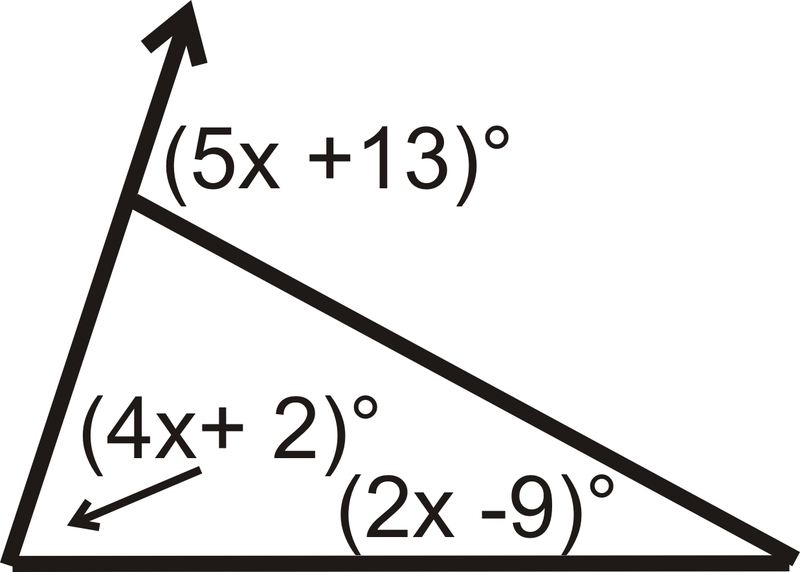
Рішення
Налаштуйте рівняння за допомогою теореми зовнішнього кута.
\(\begin{align*} \underbrace{(4x+2)^{\circ}+(2x−9)^{\circ}}_\text{remote interior angles}&=\underbrace{(5x+13)^{\circ}}_\text{exterior angle} \\ (6x−7)^{\circ}&=(5x+13)^{\circ} \\ x&=20 \end{align*}\)
Підставляємо в 20 для\(x\) того, щоб знайти кожен кут.
\([4(20)+2]^{\circ}=82^{\circ}[2(20)−9]^{\circ}=31^{\circ} \qquad Exterior \:angle:\: [5(20)+13]^{\circ}=113^{\circ}\)
Приклад\(\PageIndex{3}\)
Знайдіть міру\(\angle RQS\).
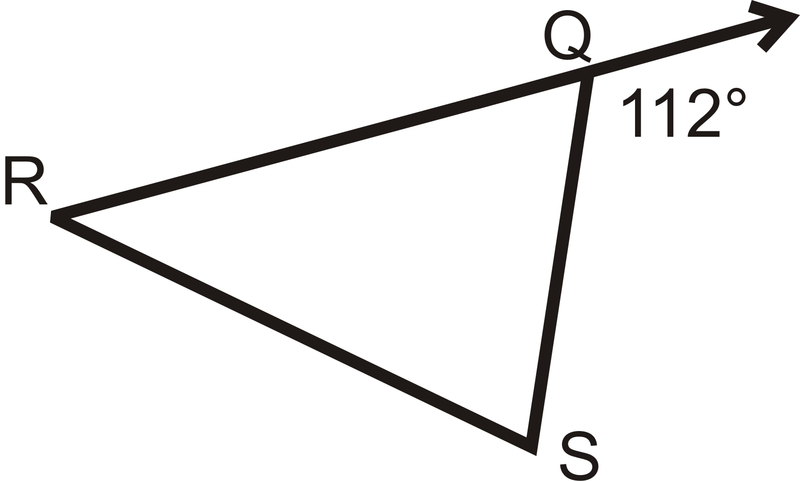Малюнок\(\PageIndex{5}\)Рішення
Зверніть увагу, що\(112^{\circ}\) є зовнішнім кутом\(\Delta RQS\) і є додатковим до\(\angle RQS\).
Налаштуйте рівняння для розв'язання відсутнього кута.
\(\begin{align*}112^{\circ}+m\angle RQS &=180^{\circ} \\ m\angle RQS&=68^{\circ}\end{align*}\)
Приклад\(\PageIndex{4}\)
Знайдіть міри нумерованих внутрішніх і зовнішніх кутів у трикутнику.
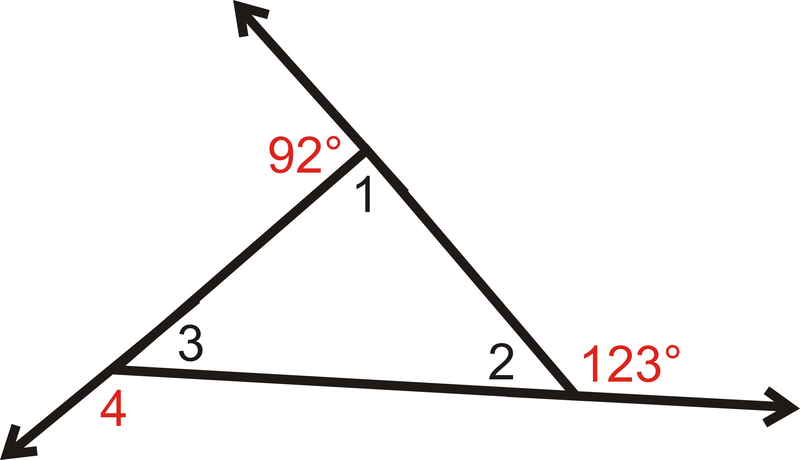Малюнок\(\PageIndex{6}\)Рішення
Ми знаємо це\(m\angle 1+92^{\circ}=180^{\circ}\) тому, що вони утворюють лінійну пару. Отже, м\ кут 1=88^ {\ circ}\).
Аналогічно,\(m\angle 2+123^{\circ}=180^{\circ}\) тому що вони утворюють лінійну пару. Отже, м\ кут 2=57^ {\ circ}\).
Ми також знаємо, що три внутрішні кути повинні складати до 180^ {\ circ}\) за теоремою про суму трикутника.
\(\begin{align*} m\angle 1+m\angle 2+m\angle 3&=180^{\circ} \qquad by\: the \:Triangle \:Sum \:Theorem. \\ 88^{\circ}+57^{\circ}+m\angle 3&=180 \\ m\angle 3&=35^{\circ}\end{align*}\)
Нарешті,\(m\angle 3+m\angle 4=180^{\circ} \qquad because\: they\: form \:a \:linear \:pair.\)
\(\begin{align*} 35^{\circ}+m\angle 4&=180^{\circ} \\ m\angle 4&=145^{\circ}\end{align*}\)
Приклад\(\PageIndex{5}\)
Яке значення\(p\) в трикутнику нижче?
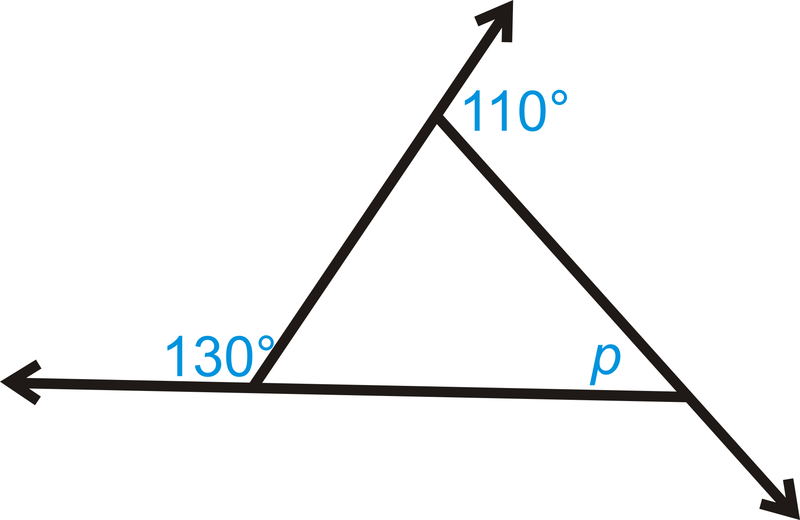
Рішення
Для початку нам потрібно знайти відсутній зовнішній кут, який ми і будемо називати\(x\). Налаштуйте рівняння за допомогою теореми про суму зовнішнього кута.
\(\begin{align*} 130^{\circ}+110^{\circ}+x&=360^{\circ} \\ x&=360^{\circ}−130^{\circ}−110^{\circ} \\ x&=120^{\circ}\end{align*} \)
\(x\)і\(p\) додати до\(180^{\circ}\) тому, що вони є лінійною парою.
\(\begin{align*} x+p&=180^{\circ} \\ 120^{\circ}+p&=180^{\circ} \\ p&=60^{\circ}\end{align*}\)
Рецензія
Визначте\(m\angle 1\).
-
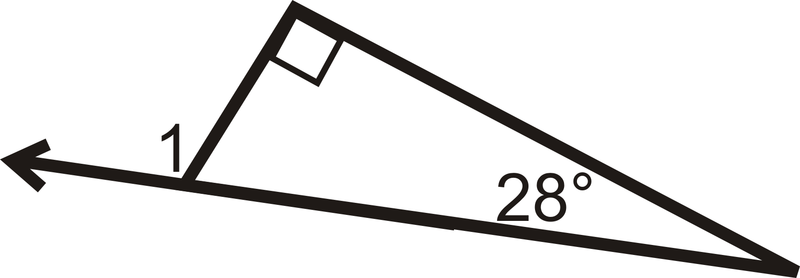
Малюнок\(\PageIndex{8}\) -
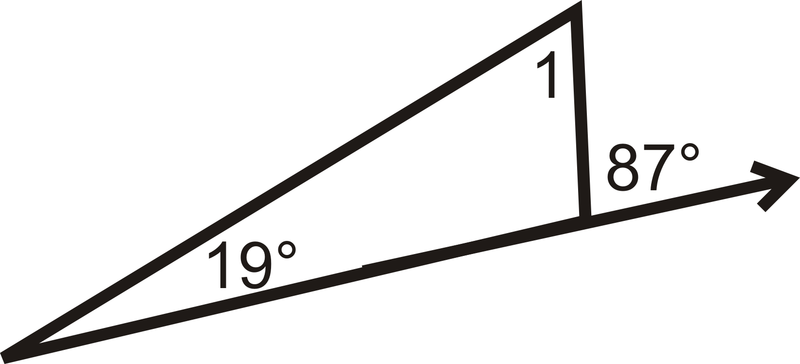
Малюнок\(\PageIndex{9}\) -
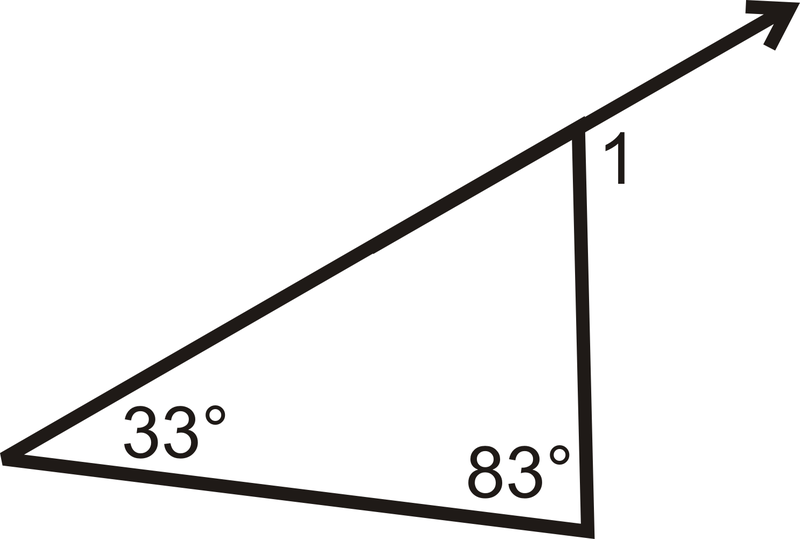
Малюнок\(\PageIndex{10}\) -
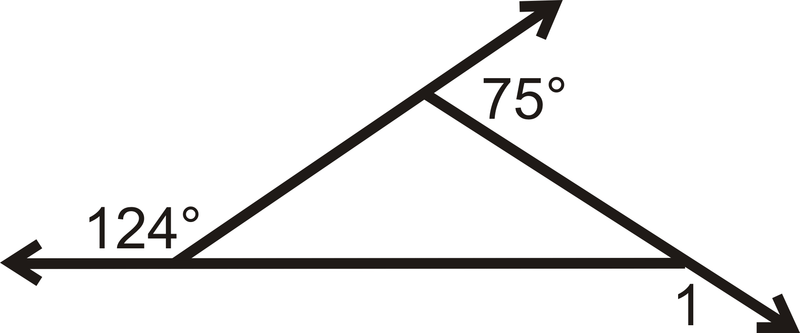
Малюнок\(\PageIndex{11}\) -
Малюнок\(\PageIndex{12}\) -
Малюнок\(\PageIndex{13}\)
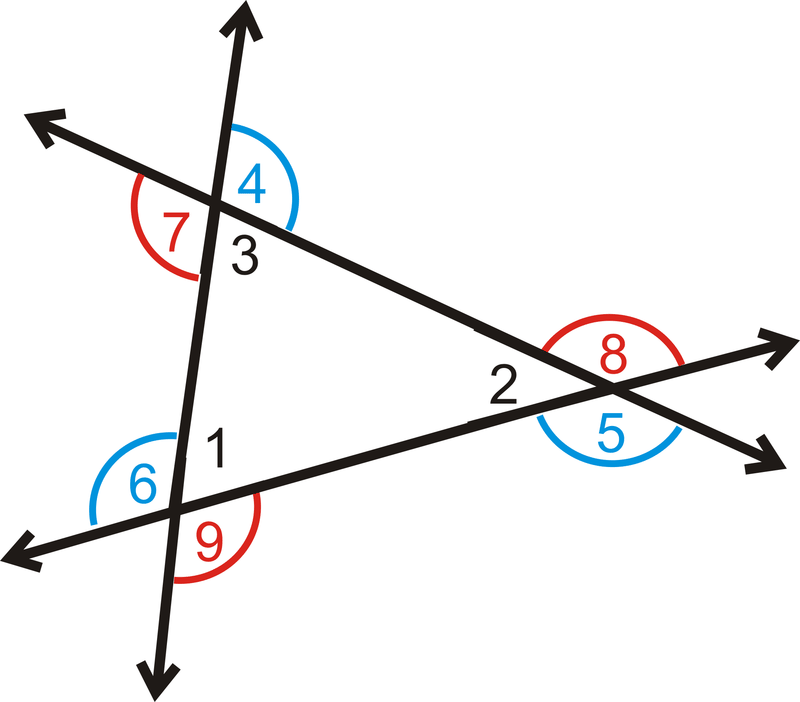
Використовуйте наступну картинку для наступних трьох проблем:
- Що таке\(m\angle 1+m\angle 2+m\angle 3\)?
- Що таке\(m\angle 4+m\angle 5+m\angle 6\)?
- Що таке\(m\angle 7+m\angle 8+m\angle 9\)?
Вирішити для\(x\).
-
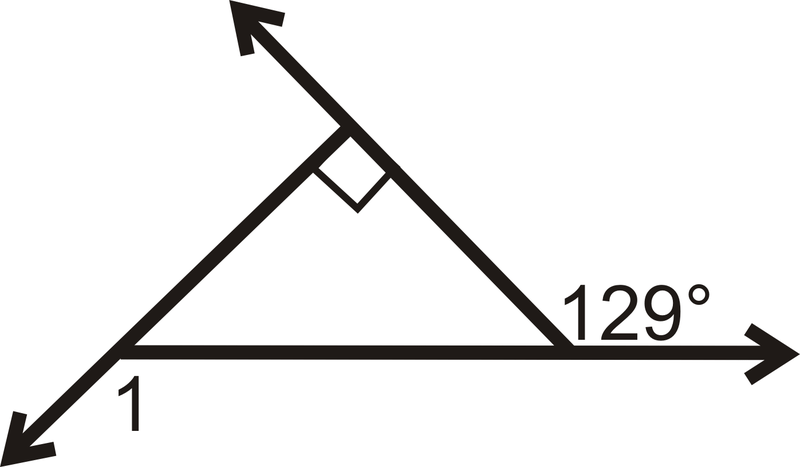
Малюнок\(\PageIndex{14}\) -
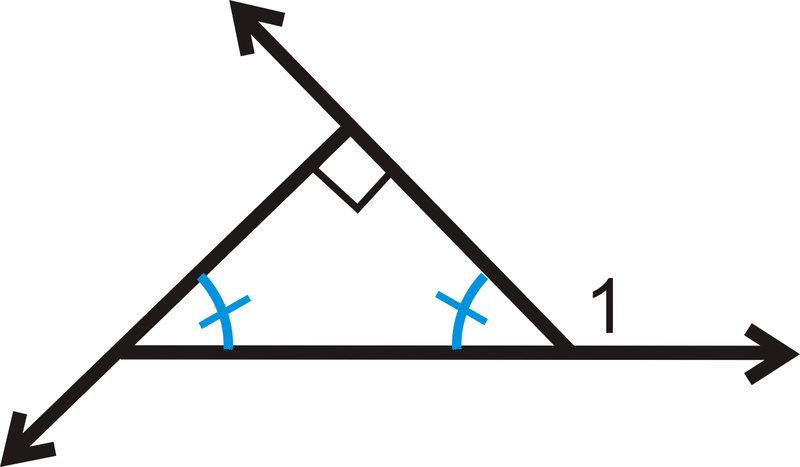
Малюнок\(\PageIndex{15}\) -
Малюнок\(\PageIndex{16}\)
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Зовнішні кути | Зовнішній кут - це кут, утворений однією стороною багатокутника і продовженням сусідньої сторони. |
| внутрішні кути | Кути на внутрішній стороні багатокутника. |
| виносні внутрішні кути | Віддалені внутрішні кути (трикутника) - це два внутрішні кути, які не примикають до зазначеного зовнішнього кута. |
| Теорема про суму трикутника | Теорема про суму трикутника стверджує, що три внутрішні кути будь-якого трикутника завжди будуть складатися до\(180^{\circ}\). |
| Теорема про суму зовнішнього кута | Теорема про зовнішню кутову суму стверджує, що зовнішні кути будь-якого багатокутника завжди додаватимуться до 360 градусів. |
Додаткові ресурси
Інтерактивний елемент
Відео: Приклади теорем про зовнішні кути - основні
Види діяльності: Зовнішні кути Теореми Обговорення Питання
Навчальні посібники: Посібник з вивчення відносин з
Практика: Зовнішні кути і теореми
Реальний світ: Теорема про зовнішні кути