4.17: Теорема про суму кута трикутника
- Page ID
- 54797
Внутрішні кути трикутника додають до 180 градусів Використовуйте рівняння, щоб знайти відсутні кутові міри, враховуючи суму 180 градусів.
Теорема про суму трикутника
Теорема про суму трикутника говорить, що три внутрішні кути будь-якого трикутника складають до\(180^{\circ}\).
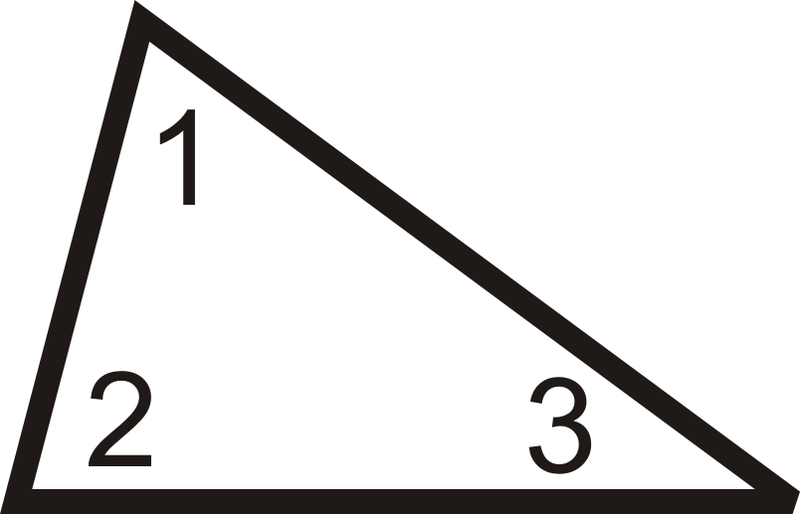
\(m\angle 1+m\angle 2+m\angle 3=180^{\circ}\).
Ось один доказ теореми про суму трикутника.
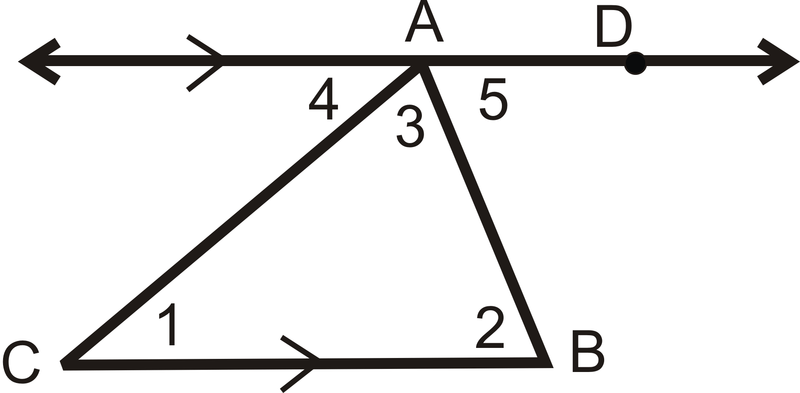
Дано:\(\Delta ABC\) з\(\overleftrightarrow{AD} \parallel \overline{BC}\)
Доведіть:\(m\angle 1+m\angle 2+m\angle 3=180^{\circ}\)
| Заява | Причина |
|---|---|
| 1. \(\Delta ABC with \overleftrightarrow{AD} \parallel \overline{BC}\) | Враховується |
| 2. \\(angle 1\cong \angle 4,\: \angle 2\cong \angle 5\) | Теорема про альтернативні внутрішні кути |
| 3. \(m\angle 1=m\angle 4,\: m\angle 2=m\angle 5\) | \ cong кути мають = заходи |
| 4. \(m\angle 4+m\angle CAD=180^{\circ}\) | Постулат лінійної пари |
| 5. \(m\angle 3+m\angle 5=m\angle CAD\) | Постулат додавання кута |
| 6. \(m\angle 4+m\angle 3+m\angle 5=180^{\circ}\) | Підміна PoE |
| 7. \(m\angle 1+m\angle 3+m\angle 2=180^{\circ}\) | Підміна PoE |
Ви можете використовувати теорему про суму трикутника, щоб знайти відсутні кути в трикутниках.
Що робити, якби ви знали, що два кути в трикутнику виміряні\(55^{\circ}\)? Як ви могли знайти міру третього кута?
Приклад\(\PageIndex{1}\)
Два внутрішніх кута трикутника вимірюють\(50^{\circ}\) і\(70^{\circ}\). Який третій внутрішній кут трикутника?
Рішення
\(50^{\circ}+70^{\circ}+x=180^{\circ}\).
Вирішіть це рівняння, і ви виявите, що третій кут є\(60^{\circ}\).
Приклад\(\PageIndex{2}\)
Знайдіть значення\(x\) і міру кожного кута.
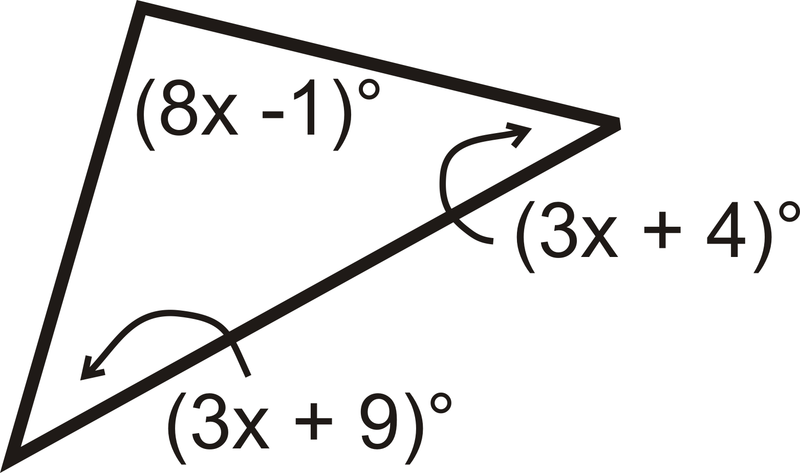
Рішення
Всі кути складаємо до\(180^{\circ}\).
\(\begin{align*} (8x−1)^{\circ}+(3x+9)^{\circ}+(3x+4)^{\circ}&=180^{\circ} \\ (14x+12)^{\circ}&=180^{\circ} \\ 14x&=168 \\ x&=12\end{align*} \)
Підставляємо в 12 для\(x\) того, щоб знайти кожен кут.
\([3(12)+9]^{\circ}=45^{\circ} \qquad [3(12)+4]^{\circ}=40^{\circ} \qquad [8(12)−1]^{\circ}=95^{\circ}\)
Приклад\(\PageIndex{3}\)
Що таке м\ кут Т?
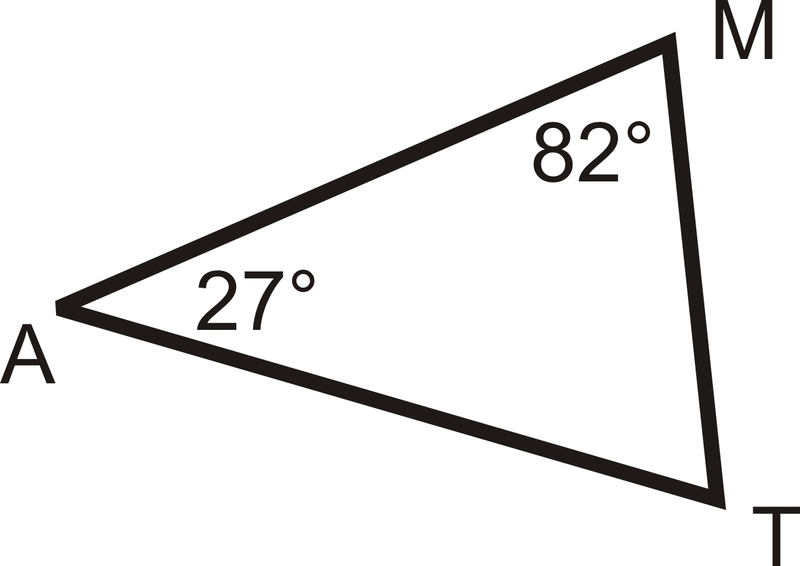
Рішення
Ми знаємо, що три кути в трикутнику повинні скласти до\(180^{\circ}\). Щоб вирішити цю задачу, налаштуйте рівняння і підставляйте в відому вам інформацію.
\(\begin{align*} m\angle M+m\angle A+m\angle T&=180^{\circ} \\ 82^{\circ}+27^{\circ}+m\angle T&=180^{\circ} \\ 109^{\circ}+m\angle T&=180^{\circ} \\ m\angle T &=71^{\circ}\end{align*}\)
Приклад\(\PageIndex{4}\)
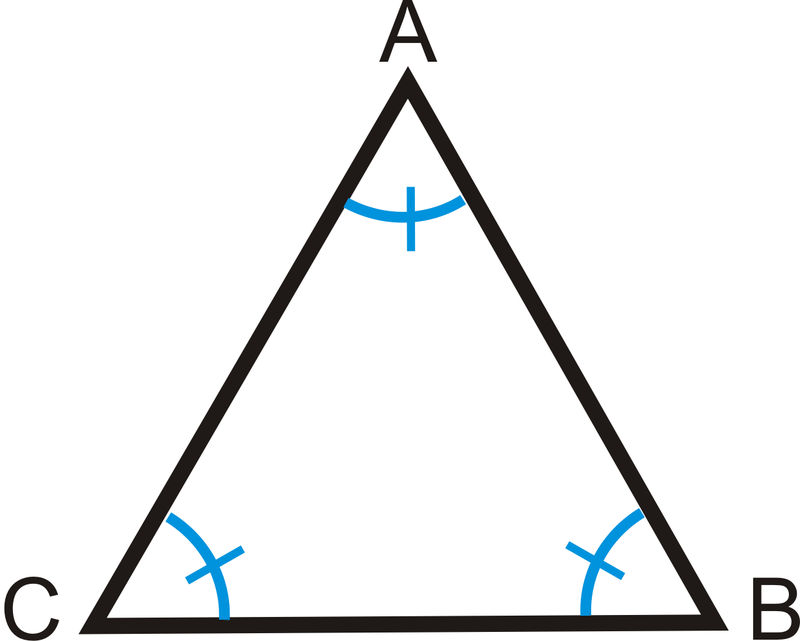
Яка міра кожного кута в рівнокутному трикутнику?
Рішення
Щоб вирішити, пам'ятайте, що\(\Delta ABC\) це рівнокутний трикутник, тому всі три кути рівні. Напишіть рівняння.
\(\begin{align*} m\angle A+m\angle B+m\angle C &=180^{\circ} \\ m\angle A+m\angle A+m\angle A&=180^{\circ} \qquad &Substitute,\: all\: angles\: are \: equal. \\ 3m\angle A&=180^{\circ} \qquad &Combine\:like \:terms. \\ m\angle A&=60^{\circ}\end{align*}\)
Якщо\(m\angle A=60^{\circ}\), то\(m\angle B=60^{\circ}\) і\(m\angle C=60^{\circ}\).
Кожен кут в рівнокутний трикутник є\(60^{\circ}\).
Приклад\(\PageIndex{5}\)
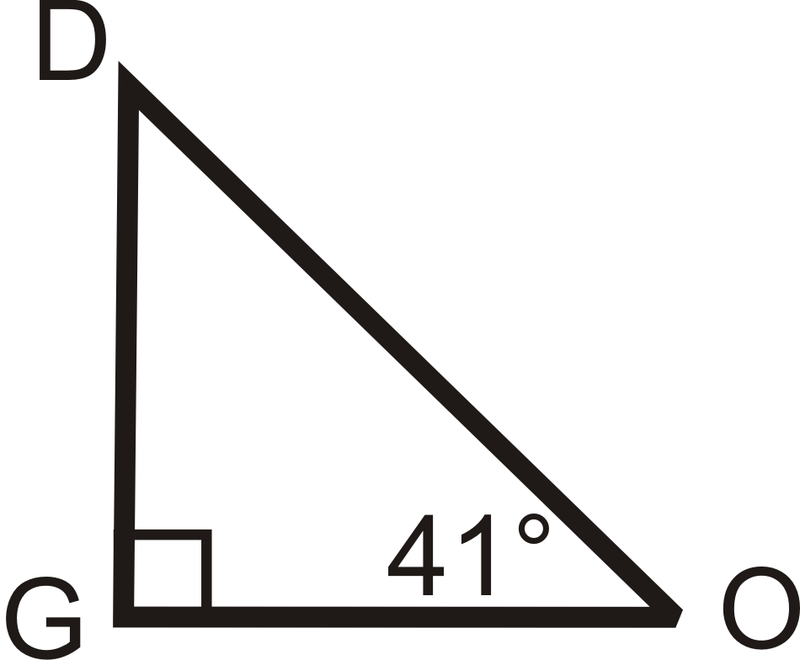
Знайдіть міру відсутнього кута.
Рішення
Ми це знаємо\(m\angle O=41^{\circ}\) і\(m\angle G=90^{\circ}\) тому, що це прямий кут. Налаштуйте рівняння, як у прикладі 3.
\(\begin{align*} m\angle D+m\angle O+m\angle G&=180^{\circ} \\ m\angle D+41^{\circ}+90^{\circ}&=180^{\circ} \\ m\angle D+41^{\circ}&=90^{\circ}\\ m\angle D=49^{\circ}\end{align*}\)
Рецензія
Визначте\(m\angle 1\) в кожному трикутнику.
1.
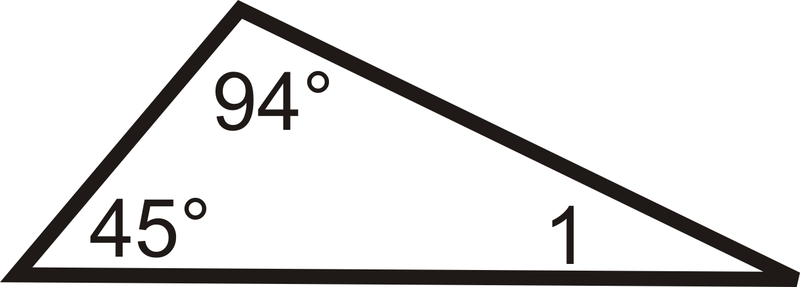
2.
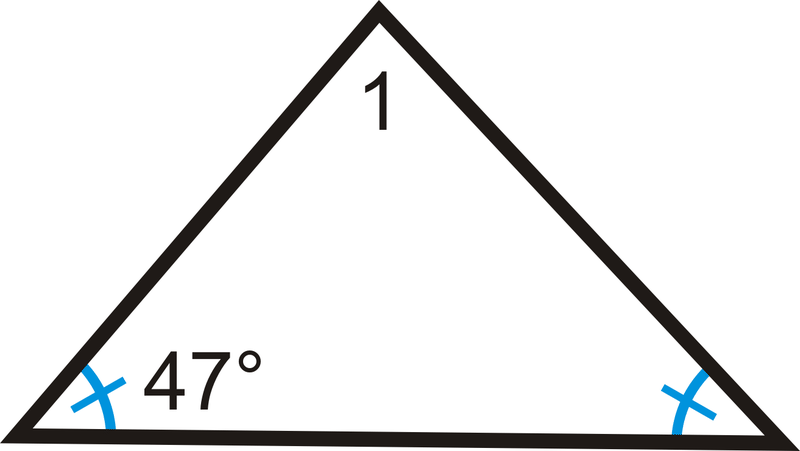
3.
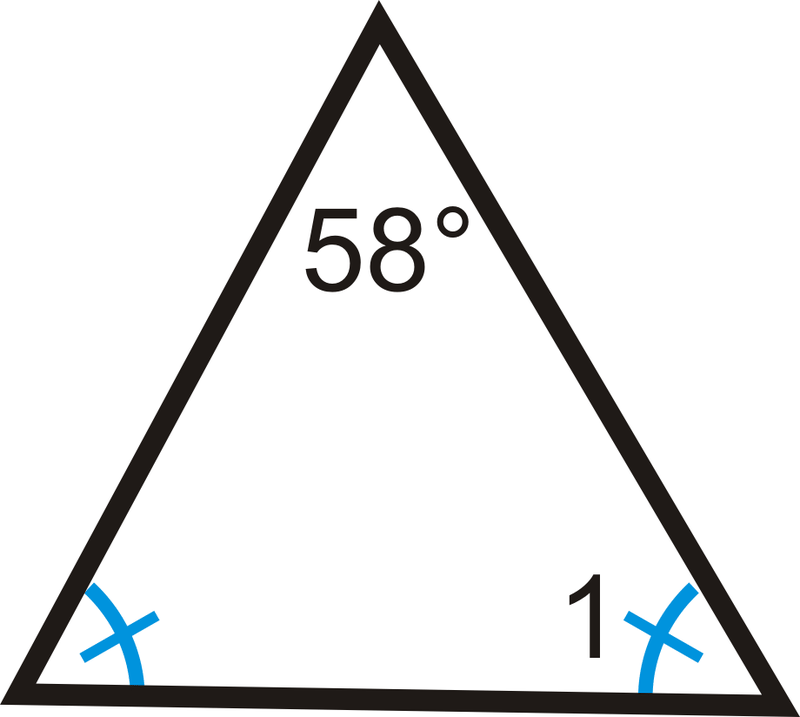
4.

5.
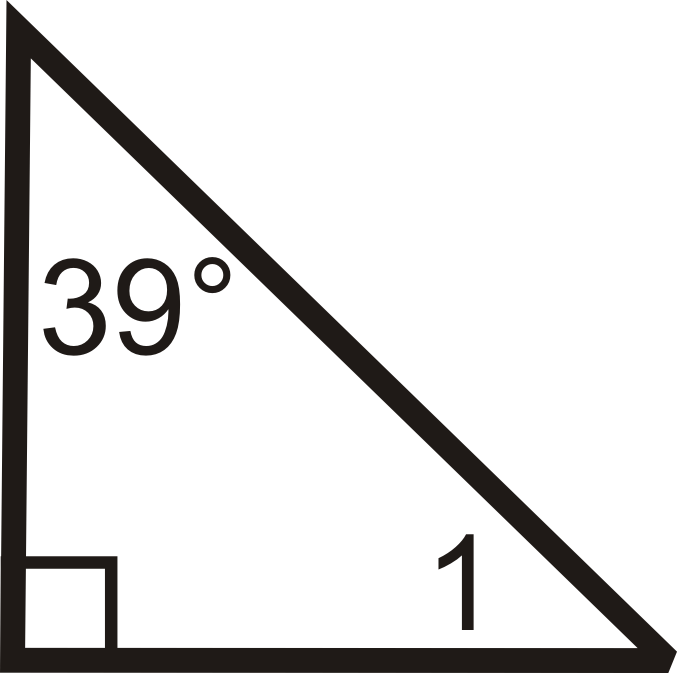
6.

7.
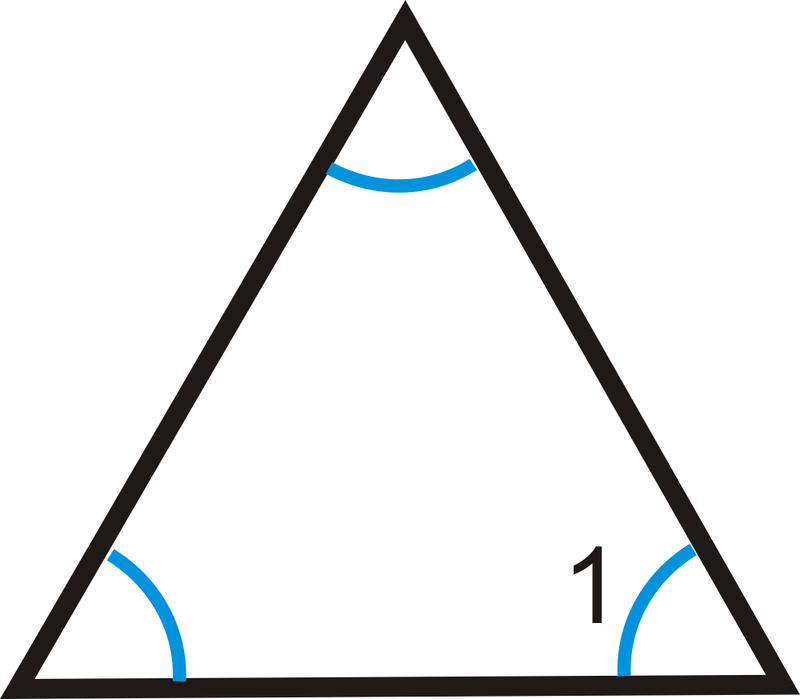
8. Два внутрішніх кута трикутника вимірюють\(32^{\circ}\) і\(64^{\circ}\). Який третій внутрішній кут трикутника?
9. Два внутрішніх кута трикутника вимірюють\(111^{\circ}\) і\(12^{\circ}\). Який третій внутрішній кут трикутника?
10. Два внутрішніх кута трикутника вимірюють\(2^{\circ}\) і\(157^{\circ}\). Який третій внутрішній кут трикутника?
Знайдіть значення\(x\) і міру кожного кута.
11.

12.
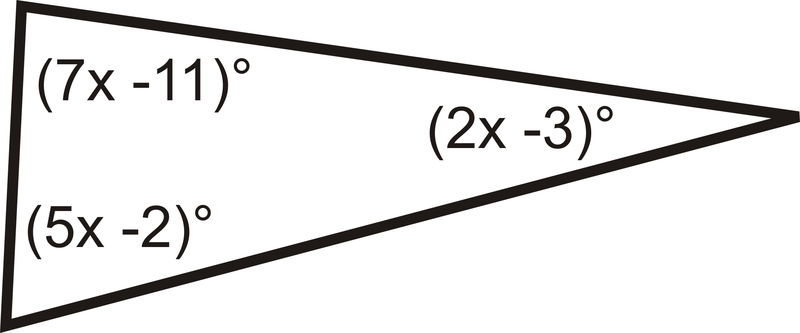
13.
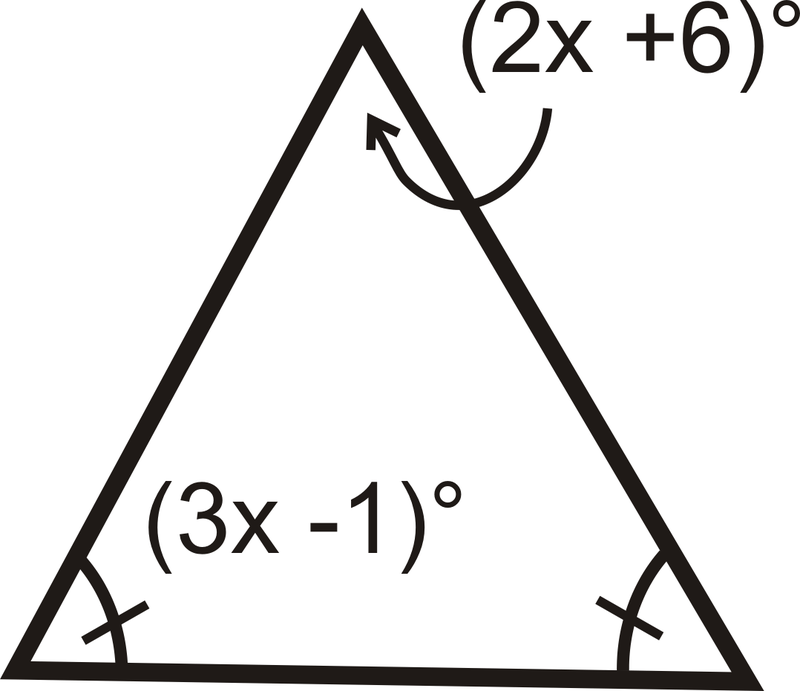
14.
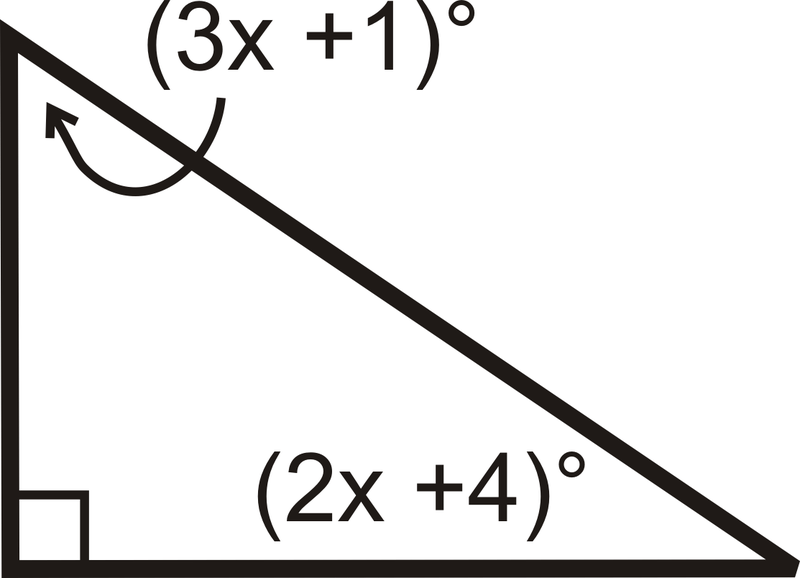
15.
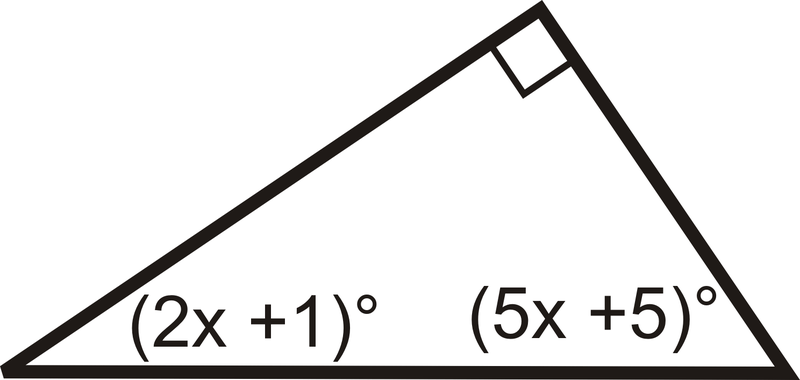
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 4.1.
Ресурси
Лексика
| Термін | Визначення |
|---|---|
| Теорема про суму трикутника | Теорема про суму трикутника стверджує, що три внутрішні кути будь-якого трикутника складають до 180 градусів. |
Додаткові ресурси
Інтерактивний елемент
Відео: Принципи теореми про суму трикутника - Основні
Види діяльності: Питання обговорення теореми суми трикутника
Навчальні посібники: Посібник з вивчення відносин з
Практика: Теорема про суму кута трикутника
Реальний світ: Теорема про суму трикутника