Skip to main content
LibreTexts - Ukrayinska

4.13: ССС

  1. Last updated
  2. Save as PDF
  • Page ID
    54805

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Три набори рівних довжин сторін визначають конгруентність.

    Бічний бічний постулат

    Якщо 3 сторони в одному трикутнику конгруентні 3 сторонам в іншому трикутнику, то трикутники конгруентні.

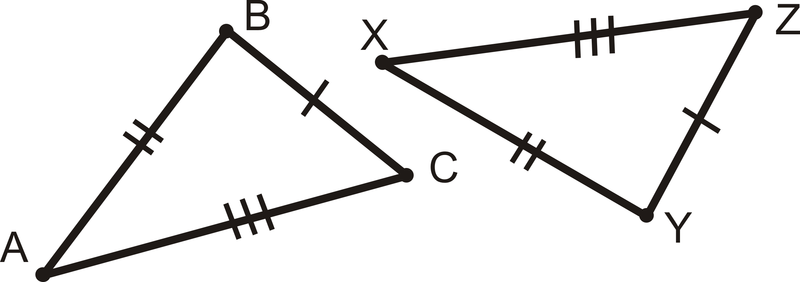
    Ф-д_9906А5Д9ЕД 0Е9Д13де де 591Ф0716 БДФ Додати С90289Ф1794Б2СБ40А98Б4Б8+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    \(\overline{BC}\cong \overline{YZ}\),\(\overline{AB}\cong \overline{XY}\), а\(\overline{AB}\cong \overline{XZ}\) потім\(\Delta ABC \cong \Delta XYZ\).

    Це називається Постулатом Side-Side (SSS), і це ярлик для доведення того, що два трикутники є конгруентними. Раніше ви повинні були показати 3 сторони і 3 кути в одному трикутнику були конгруентні 3 сторони і 3 кути в іншому трикутнику. Тепер вам потрібно лише показати 3 сторони в одному трикутнику конгруентні 3 сторони в іншому.

    Що робити, якщо вам дали два трикутника і надали інформацію тільки про їх довжині сторін? Як ви могли визначити, чи два трикутники були конгруентними?

    Приклад\(\PageIndex{1}\)

    Визначте, чи є два трикутника конгруентними.

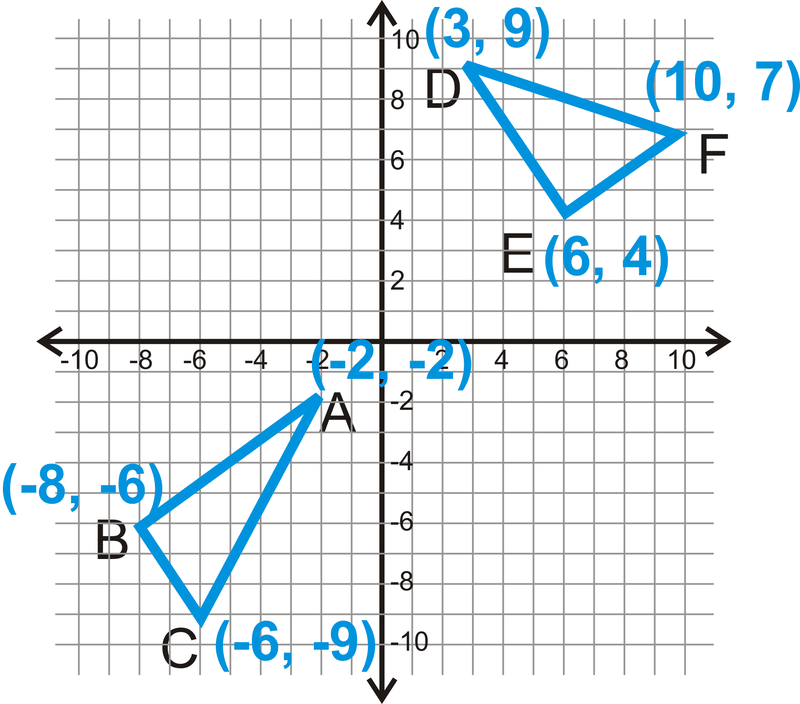
    F-D_D3623 Ф1ФС7Е489Ф75Ф8АФ 8Е02Ф Кабель 340А447224677EBD4B816C+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Рішення

    Почніть з\(\Delta ABC\).

    \(\begin{align*} AB &=\sqrt{(−2−(−8))^2+(−2−(−6))^2}\\ &=\sqrt{(6)^2+(4)^2}\\ &=\sqrt{36+16}\\ &=\sqrt{52}\\ &=\sqrt{213} \\ BC&=\sqrt{(−8−(−6))^2+(−6−(−9))^2}\\ &=\sqrt{(−2)^2+(3)^2}\\ &=\sqrt{4+9}\\ &=\sqrt{13} \\ AC&=\sqrt{(−2−(−6))^2+(−2−(−9))^2}\\ &=\sqrt{(4)^2+(7)^2}\\ &=\sqrt{16+49}\\ &=\sqrt{65} \end{align*} \)

    Тепер знайдіть сторони\(\Delta DEF\).

    \(\begin{align*} DE &=\sqrt{(3−6)^2+(9−4)^2}\\ &=\sqrt{(−3)^2+(5)^2}\\ &=\sqrt{9+25}\\ &=\sqrt{34} \\ EF&=\sqrt{(6−10)^2+(4−7)^2}\\ &=\sqrt{(−4)^2+(−3)^2}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ &=5 \\ DF&=\sqrt{(3−10)^2+(9−7)^2}\\ &=\sqrt{(−7)^2+(2)^2}\\ &=\sqrt{49+4}\\ &=\sqrt{53} \end{align*}\)

    Жодна сторона не має рівних мір, тому трикутники не є конгруентними.

    Приклад\(\PageIndex{2}\)

    Заповніть пропуски в доказі нижче.

    З огляду на:\( \overline{AB}\cong \overline{DC}\),\(\overline{AC}\cong \overline{DB}\)

    Доведіть:\(\Delta ABC\cong \Delta DCB\)

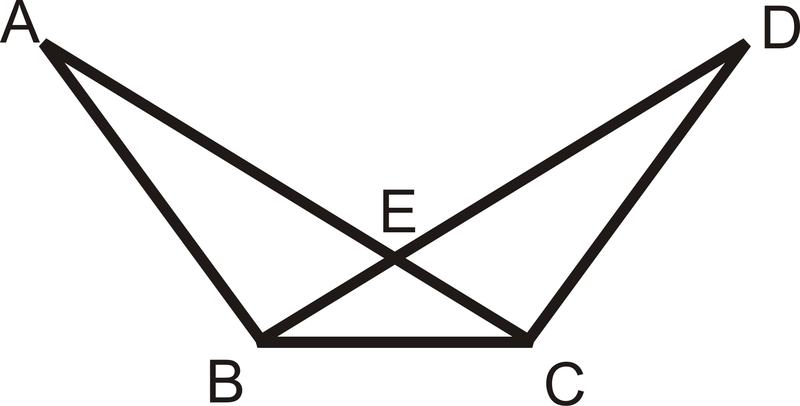    F-д_ЕД 6Б2ЕС8Б08531А60А49С17Б954Б3А9Б0ЕЕ7Ф95Б3С5863Д663018533+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)

    Рішення

    Заява Причина
    1. 1.
    2. 2. Рефлексивний\(PoC\)
    3. \(\Delta ABC\cong \Delta DCB\) 3.
    Заява Причина
    1. \(\overline{AB}\cong \overline{DC}, \overline{AC}\cong \overline{DB}\) 1. Враховується
    2. \(\overline{BC}\cong \overline{CB}\) 2. Рефлексивний\(PoC\)
    3. \(\Delta ABC\cong \Delta DCB\) 3. Постулат ССС

    Приклад\(\PageIndex{3}\)

    Напишіть заяву про конгруентність трикутника на основі малюнка нижче:

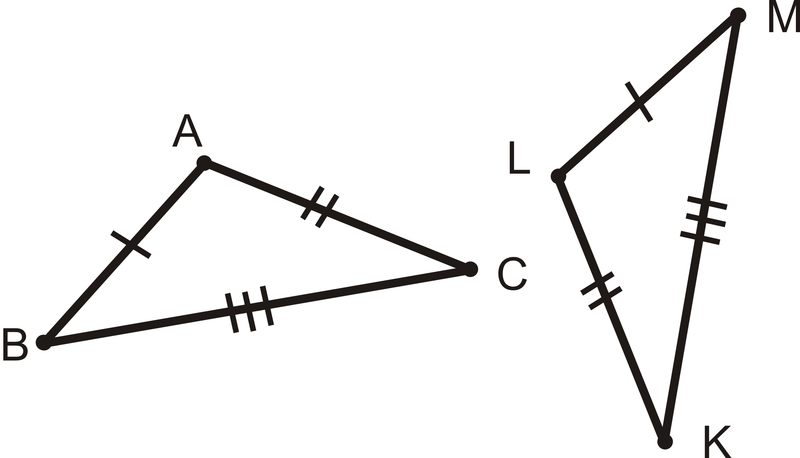    F-д_Е14Б58552ФА520Е48Е12ФЦ24Б1ДД46С4ФБ23286171426 ДК1С111168+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{5}\)

    Рішення

    З міток тик ми знаємо AB\ overline {AB}\ cong LM\ overline {AB}\), AC\ overline {AB}\ cong LK\ overline {AB}\),\ overline {BC}\ cong MK\ overline {AB}\). З Постулату ССС трикутники конгруентні. Вибудовуючи відповідні сторони, маємо\ Delta ABC\ cong\ Delta LMK\).

    Не забувайте ЗАМОВЛЕННЯ ПИТАНЬ під час написання заяв про конгруентність. Вирівняйте сторони однаковою кількістю міток tic.

    Приклад\(\PageIndex{4}\)

    Напишіть докази з двох стовпців, щоб показати, що два трикутники конгруентні.

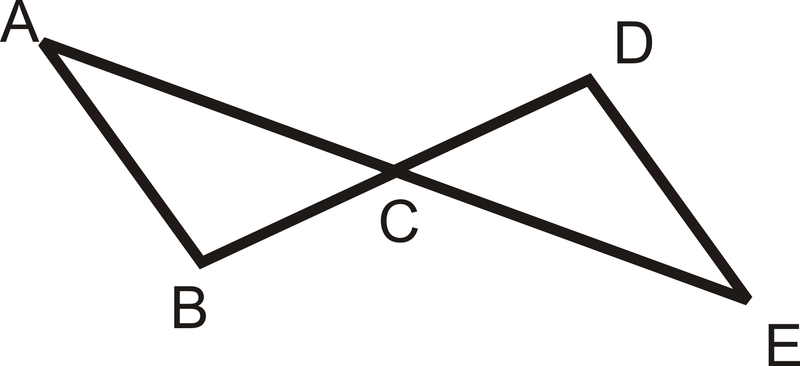    Ф-Д_БДК9Б47С6Б83591762Б3А 6505065 Ф5Ф5Ф34Д420АФФ 3432Д869А+зображення_крихіткий+зображення_крихіткий_PNGМалюнок\(\PageIndex{6}\)

    Дано:\(\overline{AB}\cong \overline{DE}\)

    \(C\)середина\(\overline{AE}\) і\(\overline{DB}\).

    Доведіть:\(\Delta ACB\cong \Delta ECD\)

    Рішення

    Заява Причина

    1. \(\overline{AB}\cong \overline{DE}\)

    \(C\)є середньою точкою\(\overline{AE} and \(\overline{DB}\)

    		 1. Дано
    2. \(\overline{AC}\cong \overline{CE}, \overline{BC}\cong \overline{CD}\) 2. Визначення середньої точки
    3. \(\Delta ACB\cong \Delta ECD\) 3. Постулат SSS

    Зверніть увагу, що ви повинні чітко вказати, що три набори сторін є конгруентними ПЕРЕД тим, як заявити, що трикутники є конгруентними.

    Приклад\(\PageIndex{5}\)

    Єдиний спосіб, яким ми покажемо, що два трикутники є конгруентними в\(x−y\) площині, - це використання SSS.

    Знайдіть довжини всіх відрізків ліній від обох трикутників, щоб побачити, чи є два трикутники конгруентними.

    Рішення

    Для цього потрібно скористатися формулою відстані.

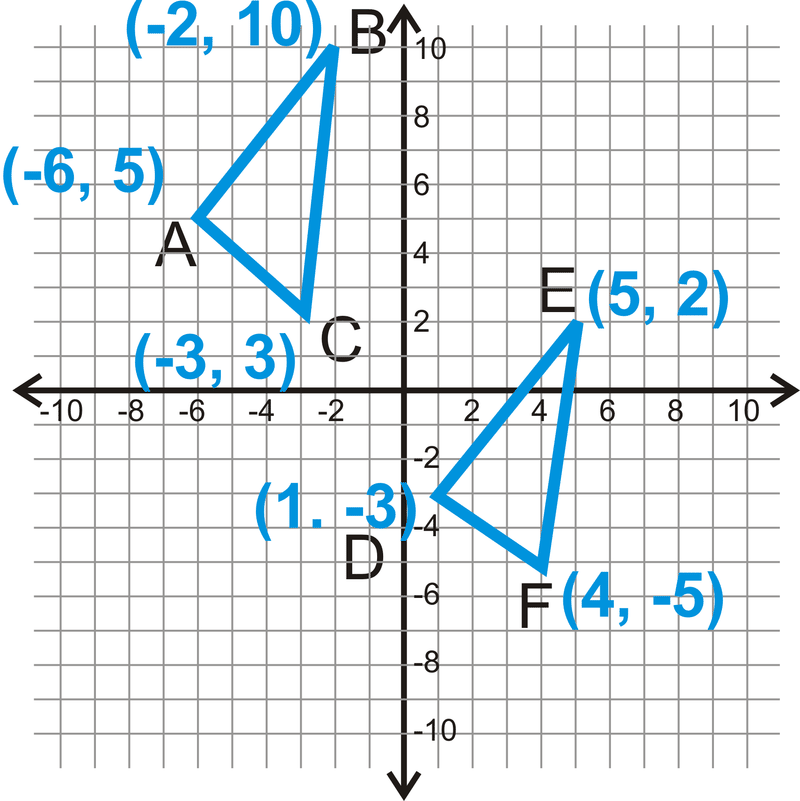
    F-D_619CFA 690Ф664 ФД1Ф35Ф3255360Ф Ф Ф 2ФЕ14 BEAC AC50F338C99967B758+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)

    Починають з\(\Delta ABC\) і його боків.

    \(\begin{align*} AB&=\sqrt{(−6−(−2))^2+(5−10)^2}\\ &=(−4)^2+(−5)^2\\ &=\sqrt{16+25}\\ &=\sqrt{41} \\ BC&=\sqrt{(−2−(−3))^2+(10−3)^2}\\ &=(1)^2+(7)^2\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=\sqrt{52} \\ AC&=\sqrt{(−6−(−3))^2+(5−3)^2}\\ &=\sqrt{(−3)^2+(2)^2}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align*}\)

    Тепер знайдіть довжини всіх сторін в\(\Delta DEF\).

    \(\begin{align*} DE&=\sqrt{(1−5)^2+(−3−2)^2}\\ &=\sqrt{(−4)^2+(−5)^2}\\ &=\sqrt{16+25}\\ &=\sqrt{41} \\ EF&=\sqrt{(5−4)^2+(2−(−5))^2}\\ &=\sqrt{(1)^2+(7)^2}\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=5\sqrt{2}\\ DF&=\sqrt{(1−4)^2+(−3−(−5))^2}\\ &=\sqrt{(−3)^2+(2)^2}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align*}\)

    \(AB=DE\), і\(BC=EF\)\(AC=DF\), таким чином, два трикутники є конгруентними по SSS.

    Рецензія

    Чи збігаються пари трикутників? Якщо так, напишіть заяву про конгруентність і чому.

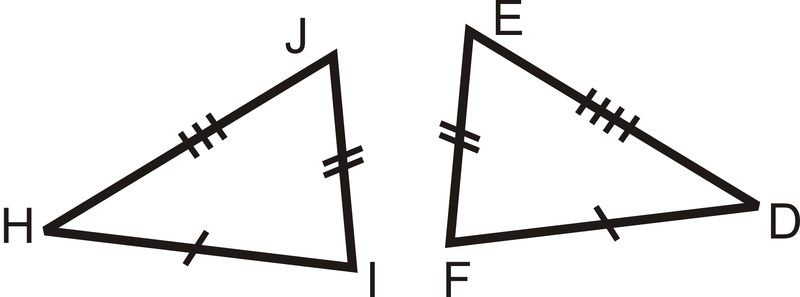
    1. F-D_2FA3C05AC23C205131DA71478E45D02AF3ФАЕ85А4 ЕЕЕ49Д5Е67+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{8}\)
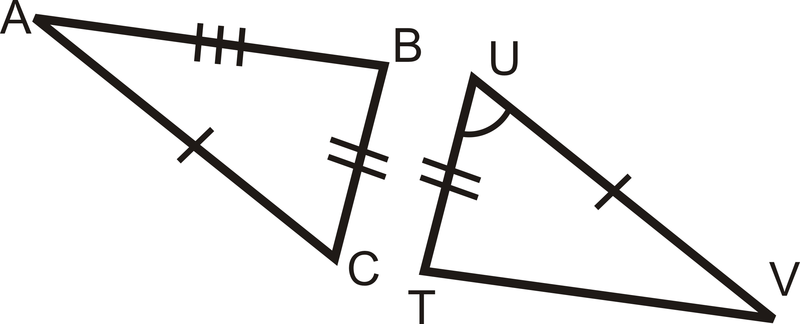
    2. Ф-Д_681975197 ФКФ 08Ф9739463Б9АЕ 87616А1АК 1Б1Ф06ЕБДФ 91988498+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{9}\)
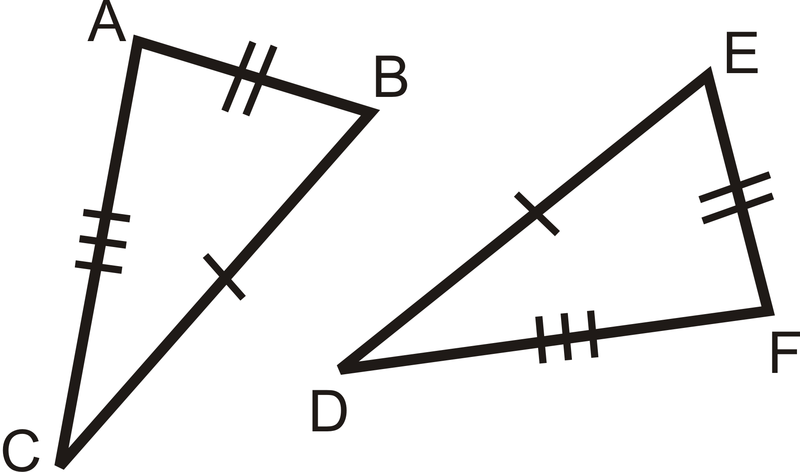
    3. F-D_8АЕ 601675Е29Б9710544 А238 ДК 2С41Д3А7Ф4720Д29С664024D462B8D+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{10}\)
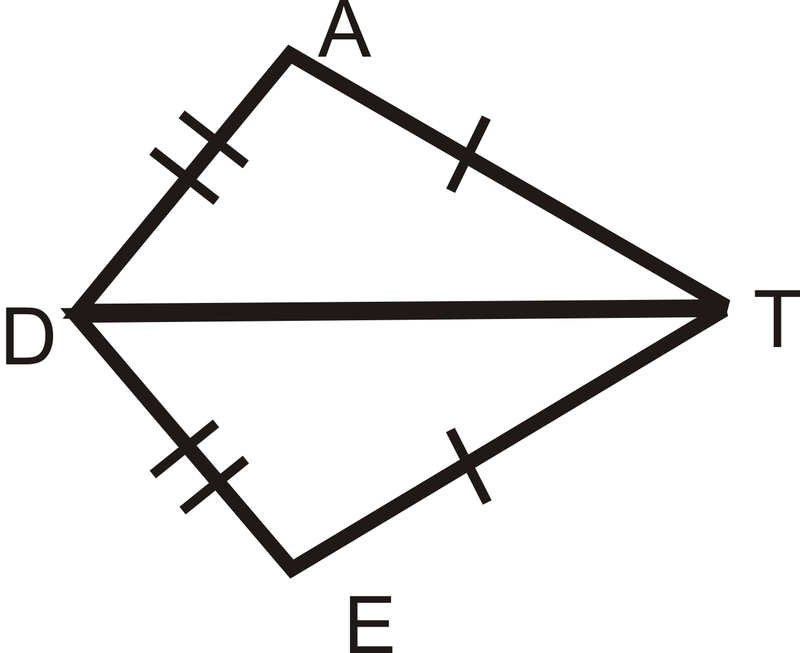    4. F-д_АС 2СА 3ДД ДЭ05 ББ2 АББ 43БД 98078д7А7Е8Б0Е8Б63622Б9Е8Ф6А28+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{11}\)

    Вкажіть додаткову інформацію, необхідну для того, щоб показати, що кожна пара трикутників є конгруентною.

    1. Використовувати SSS
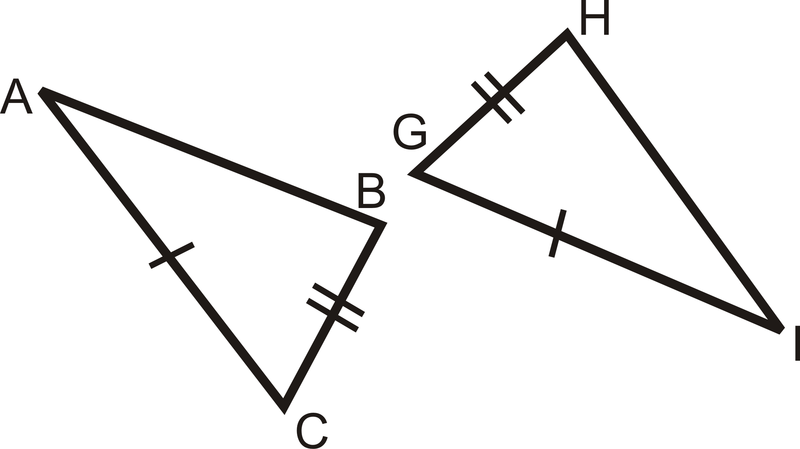      F-D_241 цеб 6317Д76 CFD44148А92Б63368 ФК3С0 Ди028Ф9Б5ФК2Д6859287+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{12}\)
    2. Використовувати SSS
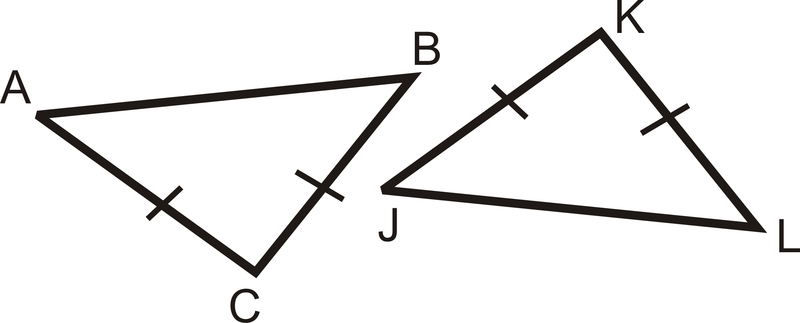      F-Д_ФК 90Б95065ДААБ 8СБ558 CFF 608472А845Б94Д58Д2372BE4E0F39+зображення_крихітка_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{13}\)

    Заповніть пропуски в докази нижче.

    1. З огляду на: B - середина\(\overline{DC} \overline{AD}\cong \overline{AC}\) Довести:\(\Delta ABD\cong \Delta ABC \)
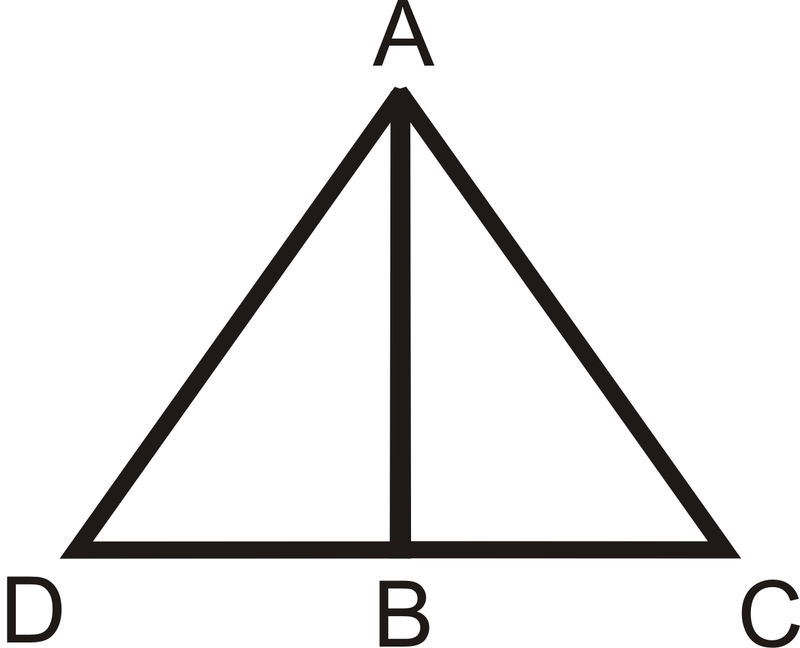
      F-D_150648577D2E3777 CAF 7E05299F91A609AC 26271341 ACD63182+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{14}\)
    Заява Причина
    1. 1.
    2. 2. Визначення середньої точки
    3. 3. Рефлексивний\(PoC\)
    4. \(\Delta ABD\cong \Delta ABC\) 4.

    Знайдіть довжини сторін кожного трикутника, щоб побачити, чи є два трикутника конгруентними. Залиште свої відповіді під радикалом.

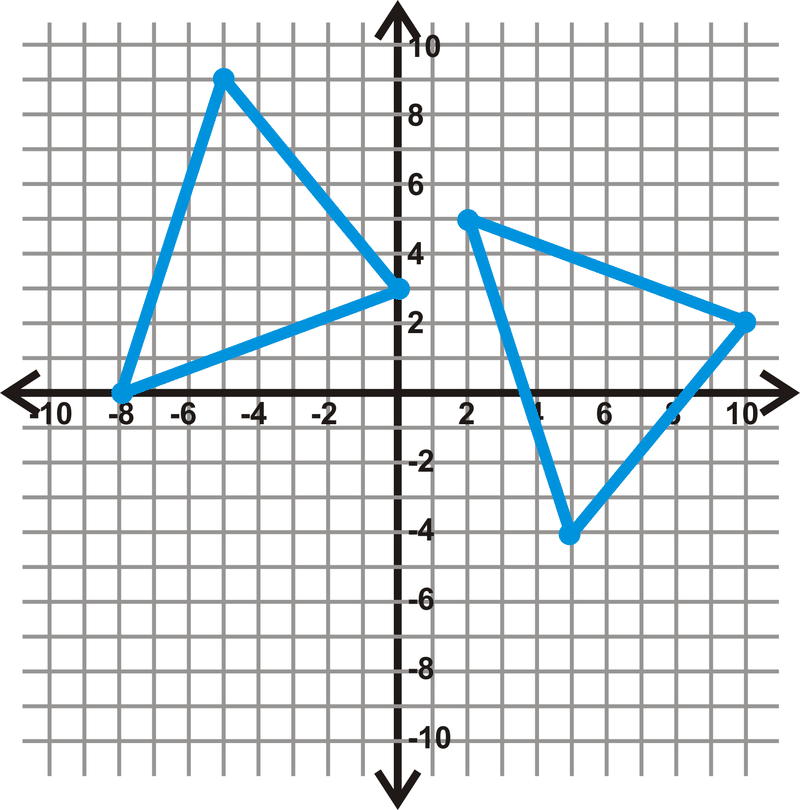
    1. F-D_532C993E268EB336ДБ3А7Е8 ФД2Ф0С5075Е5 CFD59DAA921B6CBF04B+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{15}\)
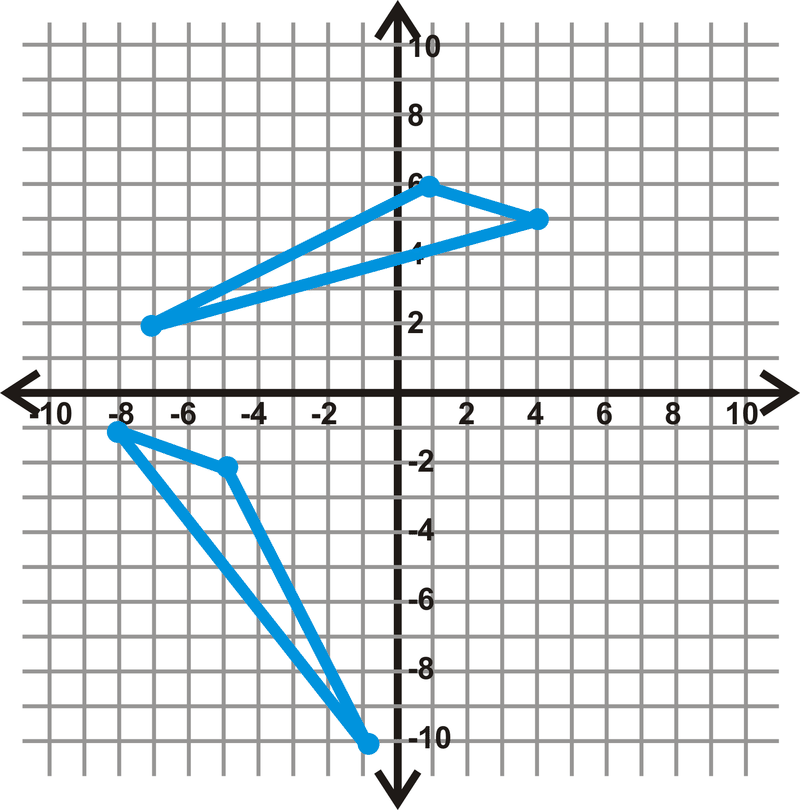
    2. F-д_де 638 де 63222FF1E34B4C4 АЕС86525121Е28ЕФ386А5А89167D666E82+зображення_крихіткий+зображення_крихіткий.PNG
      Малюнок\(\PageIndex{16}\)
    3. \(\Delta ABC: A(−1,5), B(−4,2), C(2,−2)\)і\(\Delta DEF: D(7,−5), E(4,2), F(8,−9)\)
    4. \(\Delta ABC: A(−8,−3), B(−2,−4), C(−5,−9)\)і\(\Delta DEF: D(−7,2), E(−1,3), F(−4,8)\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.6.

    Ресурси

    Лексика

    Термін Визначення
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.
    Формула відстані Відстань між двома точками\((x_1, y_1)\) і\((x_2, y_2)\) може бути визначено як\(d=(x_2−x_1)^2+(y_2−y_1)^2\).
    Теорема конгруентності H-L (гіпотенузи-ніжка) Якщо гіпотенуза і катет в одному прямокутному трикутнику конгруентні гіпотенузі і катета в іншому прямокутному трикутнику, то два трикутника конгруентні.
    Бічний бічний трикутник Бічний бічний трикутник - це трикутник, де довжини всіх трьох сторін є відомими величинами.
    ССС SSS означає сторону, сторону, сторону і відноситься до того, що всі три сторони трикутника відомі в задачі.
    Конгруентність трикутника Конгруентність трикутника виникає, якщо 3 сторони в одному трикутнику конгруентні 3 сторонам в іншому трикутнику.
    Жорстке перетворення Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Вступ до конгруентних трикутників

    Діяльність: SSS Трикутник Конгруентність обговорення Питання

    Навчальні посібники: Посібник з вивчення конгруентності три

    Практика: SSS

    Реальний світ: Конгруентність трикутника SSS