4.15: АСА та ААС

Last updated
Save as PDF

Page ID: 54811

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Два набори відповідних кутів і будь-який відповідний набір сторін доводять конгруентні трикутники.

Кут-бічний кут постулат і кут-кут-бічна теорема

Якщо два кути і одна сторона в одному трикутнику конгруентні відповідним двом кутам і одна сторона в іншому трикутнику, то два трикутника конгруентні. Ця ідея охоплює два ярлики конгруентності трикутника: кут-бічний кут і кут-кут-сторона.

Постулат конгруентності кута-бічного кута (ASA): Якщо два кути і включена сторона в одному трикутнику конгруентні двом кутам, а включена сторона в іншому трикутнику, то два трикутники конгруентні.

Теорема конгруентності кута-кута-сторона (AAS): Якщо два кути і не включена сторона в одному трикутнику конгруентні двом кутам і відповідній невключеній стороні в іншому трикутнику, то трикутники конгруентні.

Розміщення слова Side важливо, оскільки воно вказує, де сторона, яку вам дано по відношенню до кутів. Зображення нижче допомагають показати різницю між двома ярликами.

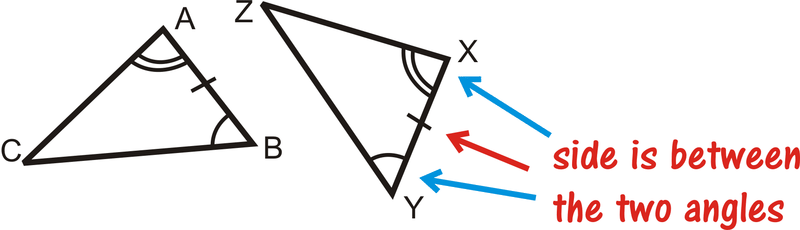
F-д_387a0f5cd927d97d4b15b14c30c0279a5d762c0302a00f36ed0817d+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

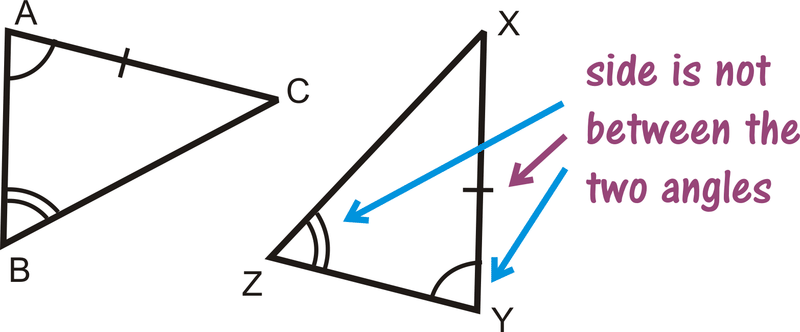
Ф-д_Е77Ф631 БФ 177 СА4 ЕДБ561 Бада 4Д53Б10С50ФБ38Б334А8 ДД3107Б106+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Що робити, якщо вам дали два трикутника і надали лише міру двох їх кутів та однієї довжини їх сторін? Як ви могли визначити, чи два трикутники були конгруентними?

Приклад\(\PageIndex{1}\)

Чи можете ви довести, що наступні трикутники є конгруентними? Чому чи чому ні?

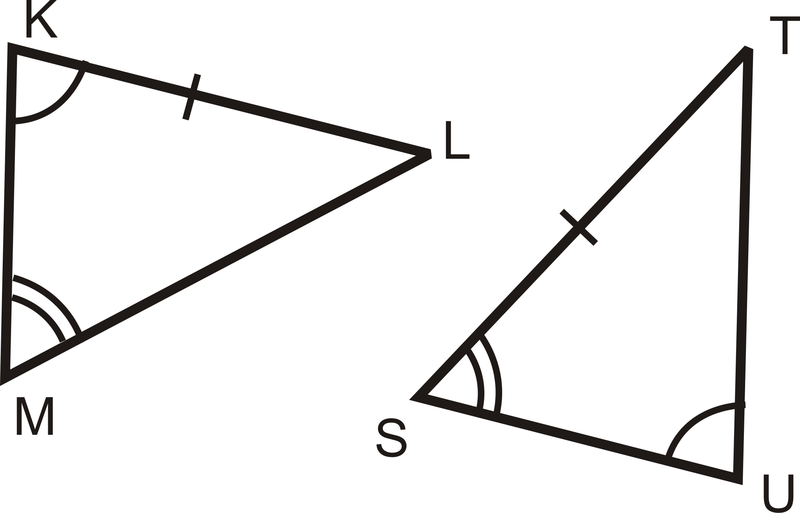
F-D_604А4 А4 АБ 66Б876C8FFF98CF5305 Деф6Е188Д3Б07574А820180E+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

Ми не можемо показати, що трикутники є\(\overline{ST}\) конгруентними, тому що\(\overline{KL}\) і не відповідають, хоча вони є конгруентними. Щоб визначити, чи\(\overline{ST}\) відповідають\(\(\overline{KL}\) і, подивіться на кути навколо них,\(\(\angle K\)\(\angle L\) і\ кут S\) і\(\angle T\). \(\angle K\)має одну дугу і\ кут L не позначений. \(\angle S\)має дві дуги і\(\angle T\) не має маркування. Для того, щоб використовувати AAS,\(\angle S\) потрібно бути конгруентним\(\angle K\).

Приклад\(\PageIndex{2}\)

Напишіть 2-стовпцеве доказ.

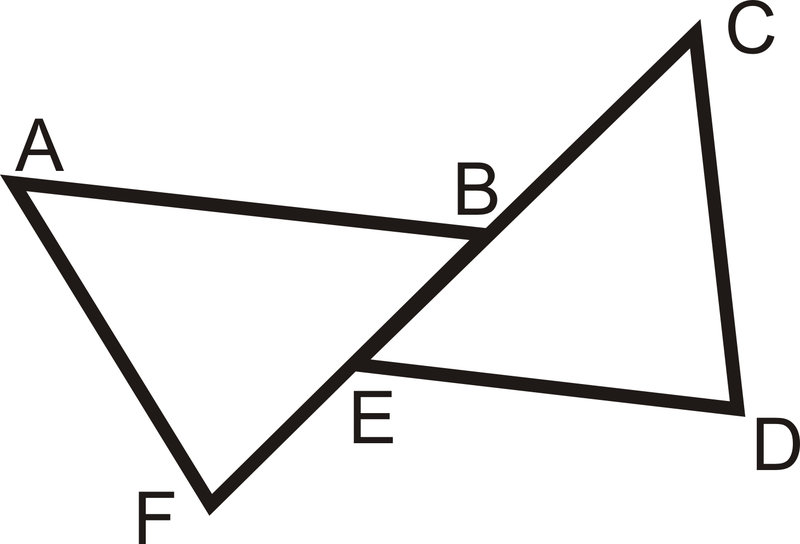
F-D_53666 БД04Д 0678 ДБ5СД 62622 ФА178 ЕКА ЕФА ФС491Ф1Б20Ф561Е5С0АФ87+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

З огляду на:\(\overline{AB}\parallel \overline{ED}\),\(\angle C\cong \angle F\),\(\overline{AB}\cong \overline{ED}\)

Доведіть:\(\overline{AF}\cong \overline{CD}\)

Рішення

*Заява*	*Причина*
1. \(\overline{AB}\parallel \overline{ED}\),\(\angle C\cong \angle F\),\(\overline{AB}\cong \overline{ED}\)	1. Враховується
2. \(\angle ABE\cong \angle DEB\)	2. Теорема про альтернативні внутрішні кути
3. \(\Delta ABF\cong \Delta DEC\)	3. АСА
4. \(\overline{AF}\cong \overline{CD}\)	4. CPCTC (відповідні частини конгруентних трикутників є конгруентними)

Приклад\(\PageIndex{3}\)

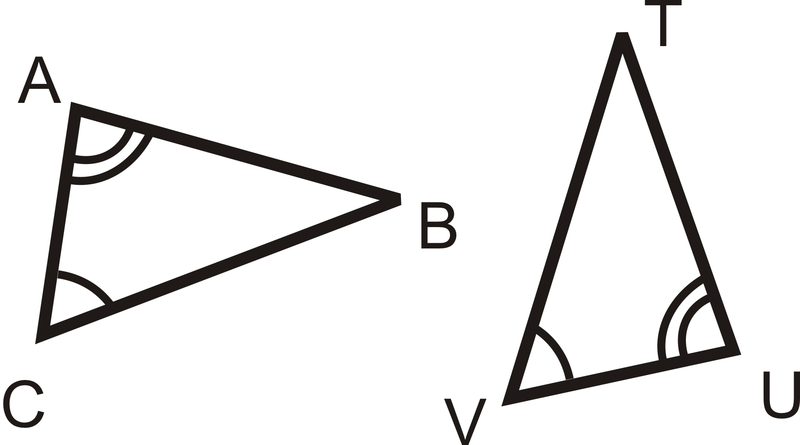
Яка інформація вам потрібна, щоб довести, що ці два трикутники є конгруентними, використовуючи Постулат ASA\(\overline{AB}\cong UT\overline{AB}\),\(\overline{AC}\cong \overline{UV}\),\(\overline{BC}\cong \overline{TV}\), або\(\angle B\cong \angle T\)?

F-D_C37D23AC282D8562DCC04E31178 ECBE419СБ15Ф4ДБ0А7Ф3А2587E9+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

Для ASA нам потрібна сторона між двома заданими кутами, яка є\(\overline{AC}\) і\(\overline{UV}\). Відповідь є\(\overline{AC}\cong \overline{UV}\).

Приклад\(\PageIndex{4}\)

Напишіть 2-стовпцеве доказ.

З огляду на:\(\angle C\cong \angle E\),\(\overline{AC}\cong \overline{AE}\)

Доведіть:\(\Delta ACF\cong \Delta AEB \)

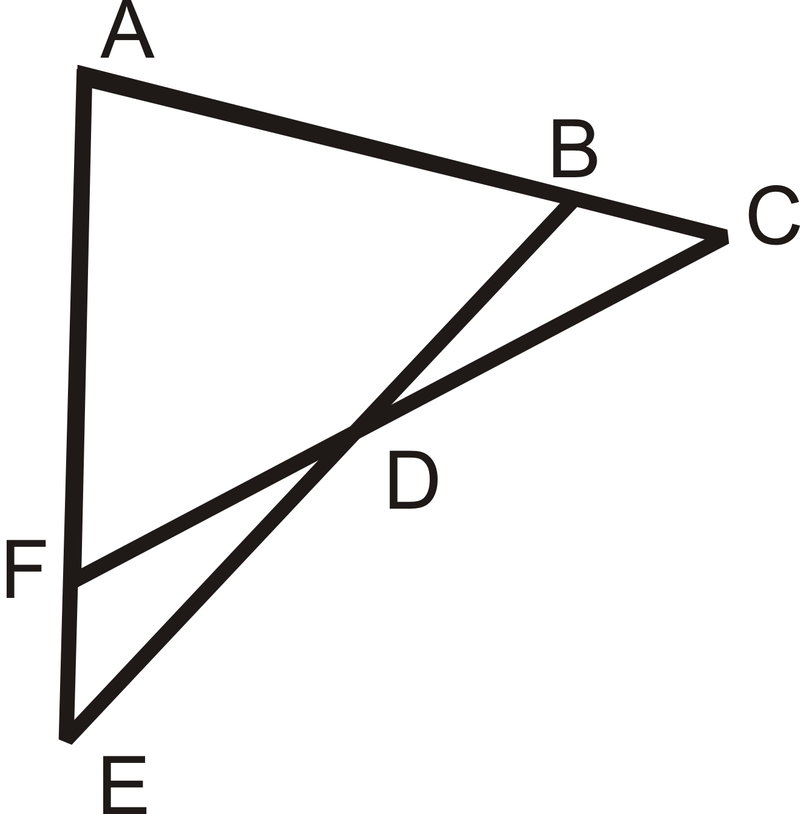
Ф-д_19СА 64Ф76Б2Д32023002С593ФДА10С05кД8Е5Ф571090 КБ40Ф8С13+зображення_крихіткий+зображення_крихіткий_крошечкий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

*Заява*	*Причина*
1. \(\angle C\cong \angle E\),\(\overline{AC}\cong \overline{AE}\)	1. Враховується
2. \(\angle A\cong \angle A\)	2. Рефлексивний\(PoC\)
3. \(\Delta ACF \cong \Delta AEB\)	3. АСА

Приклад\(\PageIndex{5}\)

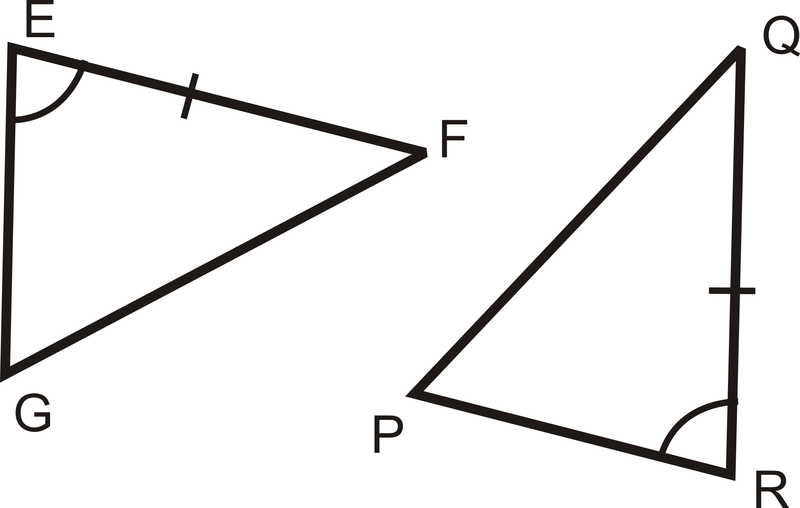
Яка інформація вам потрібна, щоб довести, що ці два трикутники конгруентні за допомогою ASA? ААС?

F-д_Е7203Д943А47Б15690А47Е22Б6Е722А980E3B179931069E4C46DEF2+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Рішення

Для ASA нам потрібні кути з іншого боку\(\overline{EF}\) і\(\overline{QR}\). \(\angle F\cong \angle Q\)

Для AAS нам знадобиться інший кут. \(\angle G\cong \angle P\)

Рецензія

З питань 1-3 визначте, чи є трикутники конгруентними. Якщо вони є, напишіть заяву про конгруентність і який постулат конгруентності або теорему ви використовували.

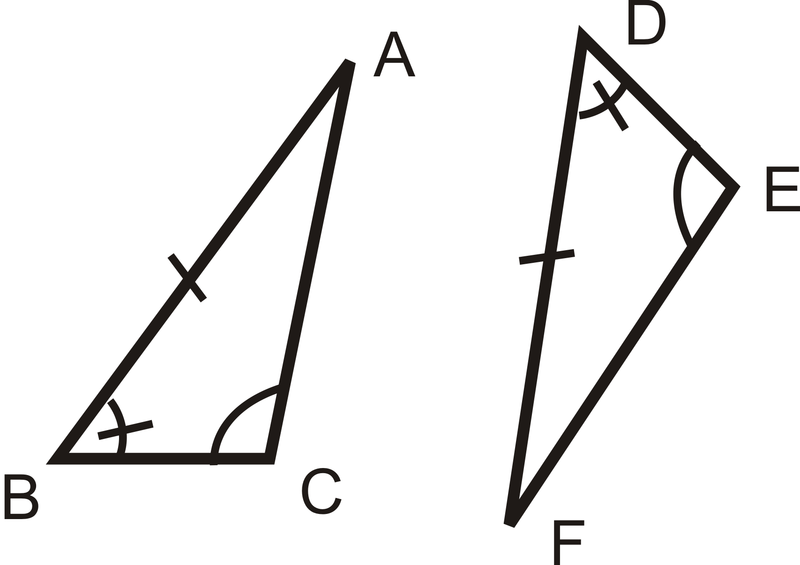
Малюнок\(\PageIndex{8}\)
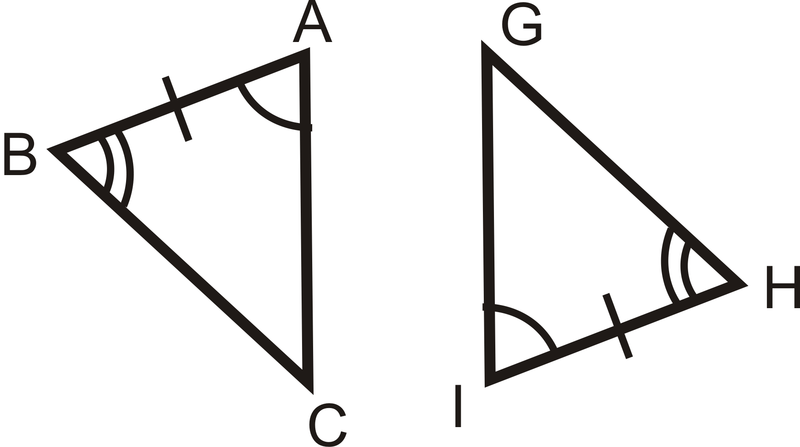
Малюнок\(\PageIndex{9}\)
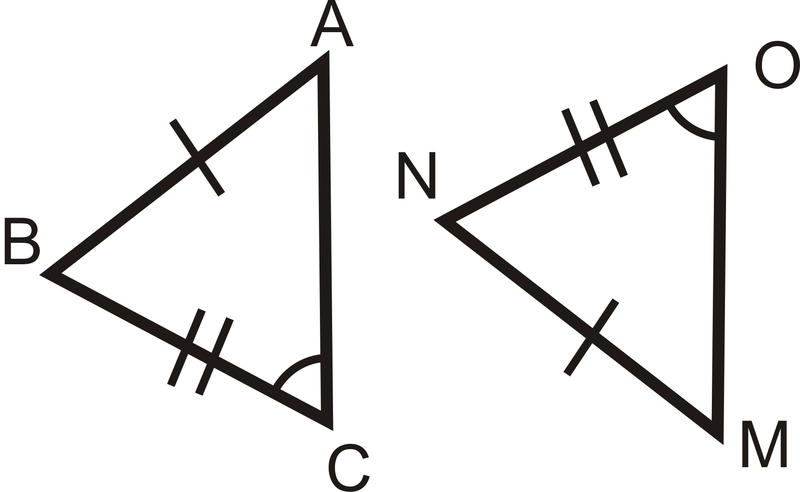
Малюнок\(\PageIndex{10}\)

Для питань 4-8 використовуйте картинку і наведену нижче інформацію.

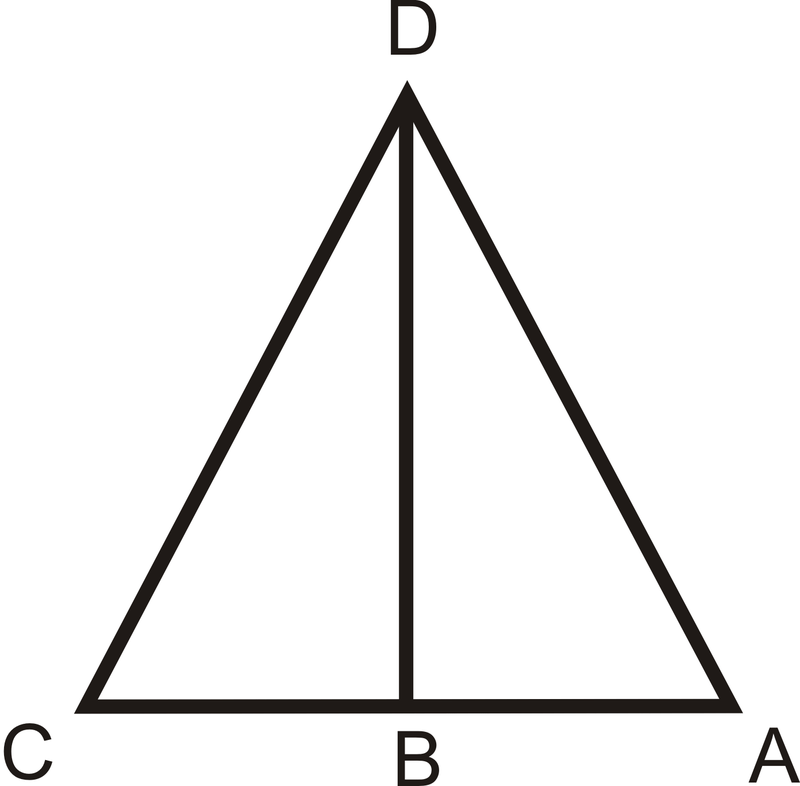
Ф-Д_Е70 БФД 46Ф7Ф52518Б052Д9 АФ 1104ЕД 20Б46С281880D5D329387D2+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{11}\)

Задано:\(\overline{DB}\perp \overline{AC}\),\(\overline{DB}\) є кутовою бісектрисою\(\angle CDA\)

З\(\overline{DB}\perp \overline{AC}\), які кути конгруентні і чому?
Тому\(\overline{DB}\) що кут бісектриса\(\angle CDA\), які два кути є конгруентними?
З погляду на картинку, яку додаткову інформацію ви даєте? Чи достатньо цього, щоб довести, що два трикутники є конгруентними?
Напишіть 2-стовпцевий доказ\(\Delta CDB\cong \Delta ADB\), щоб довести, використовуючи #4 -6.
Якою була б ваша причина\(\angle C\cong \angle A\)?

Для питань 9-13 використовуйте картинку і надану інформацію.

З огляду на:\(\overline{LP}\parallel \overline{NO}\),\(\overline{LP}\cong \overline{NO}\)

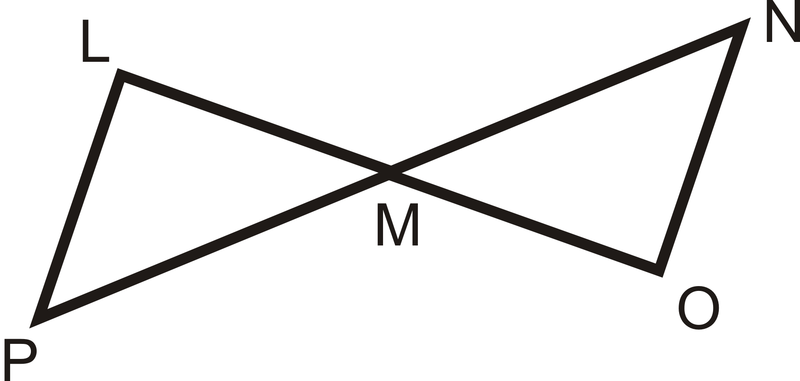
F-D_9538C6 змінного струму постійного струму 8ДБА 1D71239B6CD210A6ЕБ8 ДБКСФ 534683E9372F3CF3+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

З\(\overline{LP}\parallel \overline{NO}\), які кути конгруентні і чому?
З погляду на картину, яку додаткову інформацію ви можете зробити висновок?
Напишіть 2-стовпцевий доказ, щоб довести\(\Delta LMP\cong \Delta OMN\).
Якою була б ваша причина\(\overline{LM}\cong \overline{MO}\)?
Заповніть пропуски для доказу нижче. Використовуйте наведене зверху. Доведіть:\(M\) це середина\(\overline{PN}\).

*Заява*	*Причина*
1. \(\overline{LP}\parallel \overline{NO}\),\(\overline{LP}\cong \overline{NO}\)	1. Враховується
2.	2. Альтернативні внутрішні кути
3.	3. АСА
4. \(\overline{LM}\cong \overline{MO}\)	4.
5. \(M\)є серединою\(\overline{PN}\).	5.

Визначте додаткову інформацію, необхідну для того, щоб показати, що два трикутники збігаються за заданим постулатом.

ААС

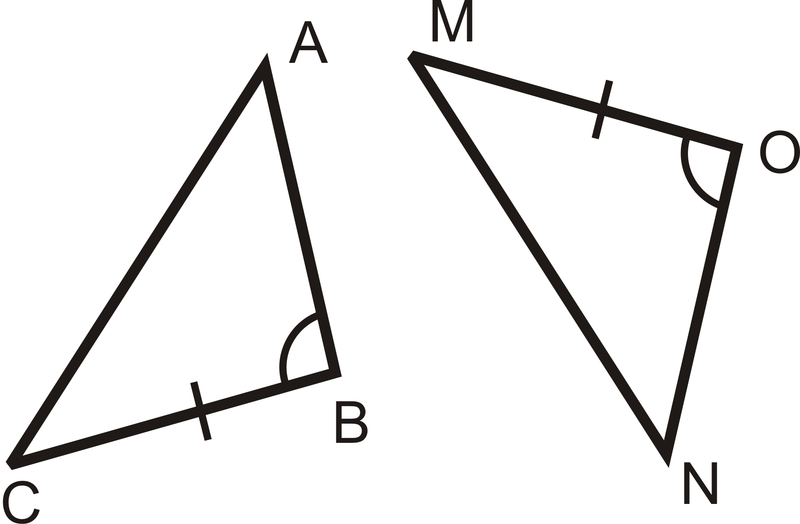
Малюнок\(\PageIndex{13}\)
ASA

Малюнок\(\PageIndex{14}\)
ASA

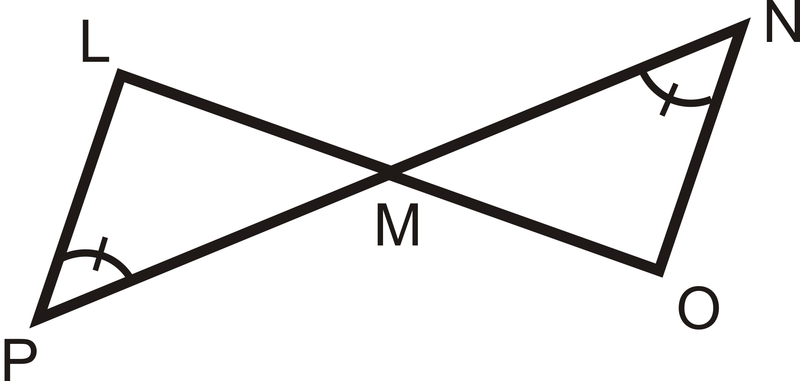
Малюнок\(\PageIndex{15}\)
ААС

Малюнок\(\PageIndex{16}\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.8.

Ресурси

Лексика

Термін	Визначення
CPCTC	*Відповідні частини конгруентних трикутників є конгруентними*. Він використовується для показу двох сторін або двох кутів у трикутниках конгруентні після того, як довів, що трикутники є конгруентними.
AAS (кут-кут-сторона)	Якщо два кути і не включена сторона в одному трикутнику конгруентні двом кутам, а відповідна не включена сторона в іншому трикутнику, то трикутники конгруентні.
Кут бічний кут трикутника	Термін «кутовий трикутник» відноситься до трикутника з відомими мірами двох кутів і довжини сторони між ними.
ASA	ASA, кут-бічний кут, відноситься до двох відомих кутів у трикутнику з однією відомою стороною між відомими кутами.
Конгруентний	Конгруентні фігури ідентичні за розміром, формою і мірою.
Конгруентність трикутника	Конгруентність трикутника виникає, якщо 3 сторони в одному трикутнику конгруентні 3 сторонам в іншому трикутнику.
Жорстке перетворення	Жорстке перетворення - це перетворення, яке зберігає відстань і кути, воно не змінює розмір або форму фігури.

Додаткові ресурси

Відео: Вступ до конгруентних трикутників

Діяльність: ASA і AAS Трикутник Конгруентність обговорення питання

Навчальні посібники: Посібник з вивчення конгруентності три

Практика: ASA та AAS

Реальний світ: Конгруентність трикутника SSS