4.12: Конгруентні трикутники
- Page ID
- 54902
Перевірте відповідність SSS, SAS, RHS та ASA
Застосування конгруентних трикутників
Два трикутника є конгруентними тоді і тільки тоді, коли відповідні пари сторін і відповідні пари є конгруентними.
Наступний список узагальнює різні критерії, які можуть бути використані для відображення конгруентності трикутника:
- AAS (кут-кут-сторона): Якщо два трикутники мають дві пари конгруентних кутів, а незагальна сторона кутів в одному трикутнику конгруентна відповідній стороні в іншому трикутнику, то трикутники конгруентні.
- ASA (кут-бічний кут): Якщо два трикутники мають дві пари конгруентних кутів, а загальна сторона кутів (сторона між конгруентними кутами) в одному трикутнику конгруентна відповідній стороні в іншому трикутнику, то трикутники конгруентні.
- SAS (Side-Angle-Side): Якщо два трикутники мають дві пари конгруентних сторін, а включений кут в один трикутник конгруентний включеному куту в іншому трикутнику, то трикутники конгруентні.
- SSS (Side-Side): Якщо два трикутники мають три пари конгруентних сторін, то трикутники конгруентні.
- Лише правильні трикутники: HL (Гіпотенуза-Ніг): Якщо два правильних трикутника мають одну пару катетів конгруентні та гіпотенузи конгруентні, то трикутники конгруентні.
Якщо два трикутника не задовольняють хоча б одному з наведених вище критеріїв, ви не можете бути впевнені, що вони збігаються.
Інтерактивний елемент
Визнання перпендикулярних бісектрис
У трикутнику нижче\ overline {BC} - перпендикулярна бісектриса AD\ overline {AB}. Тому\ overline {AC}\ cong\ overline {CD}. Крім того, м\ кут ACB = 90^ {\ circ} і м\ кут DCB=90^ {\ circ}, так\ кут ACB\ cong\ кут DCB. Ви також знаєте, що\ overline {BC} є стороною обох трикутників, і явно конгруентна собі (це називається рефлексивним властивістю).

Трикутники конгруентні по SAS. Зверніть увагу, що хоча це правильні трикутники, ви не використовуватимете HL для показу конгруентності трикутника в цьому випадку, оскільки вам не дано, що гіпотенуси є конгруентними.
Вимірювання кутів
Використовуючи інформацію з попередньої проблеми, якщо\(m\angle A=50^{\circ}\), що таке\(m\angle D\)?
\(m\angle D=50^{\circ}\)
Оскільки трикутники конгруентні, всі їхні відповідні кути та сторони повинні бути конгруентними. \ кут A\) і\ кут D\) є відповідними кутами, так що\(\angle A\cong \angle D\).
Конгруентні трикутники
Чи одна діагональ прямокутника ділить прямокутник на конгруентні трикутники?
- Нагадаємо, що прямокутник - це чотирикутник з чотирма прямими кутами.
- Протилежні сторони прямокутника конгруентні.

Існує більш ніж достатньо інформації, щоб показати, що\ (\ Delta EFG\ cong\ Delta GHE)\.
- Метод #1: Трикутники мають три пари конгруентних сторін, тому вони конгруентні SSS.
- Метод #2: Трикутники мають дві пари конгруентних сторін і конгруентні включені кути, тому вони конгруентні SAS.
- Метод #3: Трикутники - це прямі трикутники з конгруентними гіпотенузами та парою конгруентних катетів, тому вони конгруентні по HL.
Приклад\(\PageIndex{1}\)
Макс будує трикутник за допомогою онлайн-інструменту. Він розповідає Алісії, що його трикутник має кут 42^ {\ circ}, сторону довжини 12 і сторону довжини 8. Маючи лише цю інформацію, чи зможе Алісія побудувати трикутник, який повинен бути конгруентним трикутнику Макса?
Рішення
Якби Макс також сказав Алісії, що кут знаходиться між двома сторонами, то вона зможе побудувати трикутник, який повинен бути конгруентним завдяки SAS. Якщо кут не між двома сторонами, вона не може бути впевнена, що її трикутник є конгруентним, оскільки SSA не є критерієм конгруентності трикутника. Оскільки Макс не заявив, де кут стосовно сторін, Алісія не може створити трикутник, який повинен бути конгруентним трикутнику Макса.
Приклад\(\PageIndex{2}\)
Чи є наступні трикутники конгруентними? Поясніть.

Рішення
Зверніть увагу, що крім однієї пари конгруентних сторін і однієї пари конгруентних кутів,\(\overline{AC}\cong \overline{CA}\).
\(\Delta ACB\cong \Delta CAD\)по SAS.
Приклад\(\PageIndex{3}\)
Чи є наступні трикутники конгруентними? Поясніть.
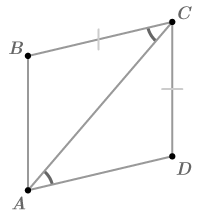
Рішення
Конгруентні сторони не відповідають так само, як відповідні конгруентні кути. Дана інформація для\(\Delta ACB\) SAS, тоді як дана інформація для\(\Delta CAD\) SSA. Трикутники не обов'язково конгруентні.
Приклад\(\PageIndex{4}\)
\(G\)є середньою точкою\(\overline{EH}\). Чи є наступні трикутники конгруентними? Поясніть.

Рішення
Тому що G\) є середньою точкою\(\overline{EH}\),\(\overline{EG}\cong \overline{GH}\). Ви також знаєте, що\(\angle EGF\cong \angle HGI\) тому, що вони є вертикальними кутами. \(\Delta EGF\cong \Delta HGI\)по ASA.
Рецензія
1. Перерахуйте п'ять критеріїв конгруентності трикутника і намалюйте малюнок, який демонструє кожен.
2. Враховуючи два трикутники, чи завжди вам потрібно принаймні три частини інформації про кожен трикутник, щоб мати можливість стверджувати, що трикутники є конгруентними?
Для кожної пари трикутників скажіть, чи достатньо наведеної інформації, щоб показати, що трикутники конгруентні. Якщо трикутники конгруентні, вкажіть критерій, який ви використовували для визначення конгруентності, і напишіть заяву конгруентності.
Зверніть увагу, що зображення не обов'язково малюються в масштабі.
3.
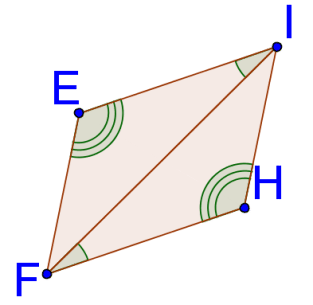
4.
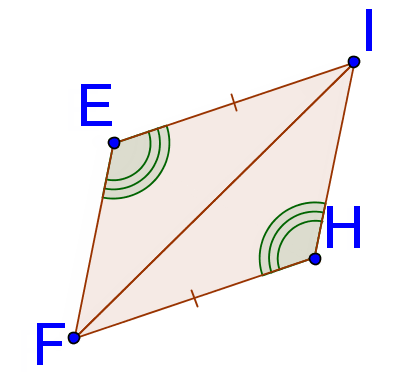
5.
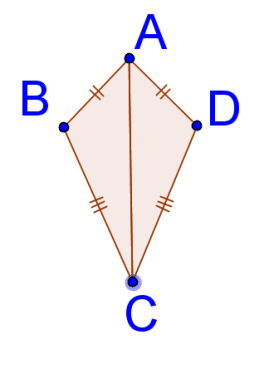
6.
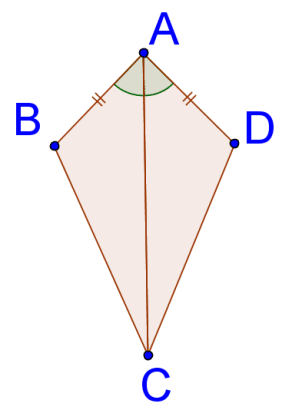
7.
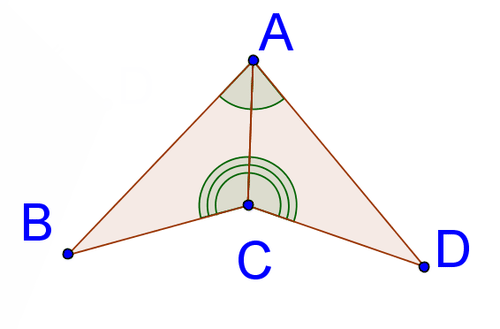
8.
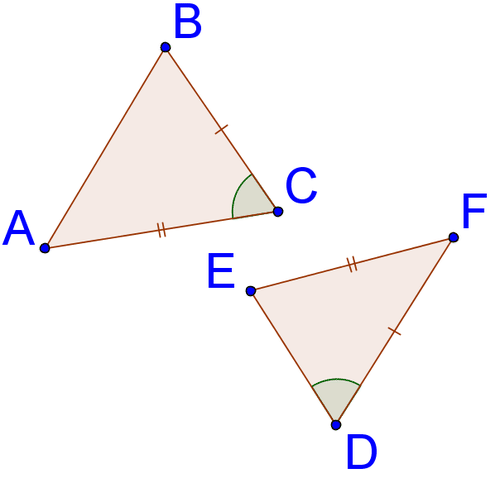
Для 9-11 вкажіть, чи достатньо заданої інформації про прихований трикутник для побудови трикутника, який повинен бути конгруентним із прихованим трикутником. Поясніть свою відповідь.
9. \(\Delta ABC\)з\(m\angle A=72^{\circ},\: AB=6 \:cm, \:BC=8 \:cm.\)
10. \(\Delta ABC\)з\(m\angle A=90^{\circ},\: AB=4 \:cm, \:BC=5 \:cm.\)
11. \(\Delta ABC\)з\(m\angle A=72^{\circ},\: AB=6 \:cm, \:AC=8 \:cm.\)
12. Нагадаємо, що квадрат - це чотирикутник з чотирма прямими кутами і чотирма конгруентними сторонами. Покажіть і поясніть, чому діагональ квадрата ділить квадрат на два конгруентних трикутника.
13. Покажіть та поясніть, використовуючи інший критерій конгруентності трикутника, чому діагональ квадрата ділить квадрат на два конгруентні трикутники.
14. Нагадаємо, що повітряний змій - це чотирикутник з двома парами суміжних, конгруентних сторін. Чи розділить одна з діагоналей повітряного змія на два конгруентних трикутника? Покажіть і поясніть свою відповідь.
15. На малюнку нижче,\(G\) це середина обох\(\overline{EH}\) і\(\overline{FI}\). Поясніть, чому\(\overline{FH}\cong \overline{IE}\) і\(\overline{FE}\cong \overline{HI}\).
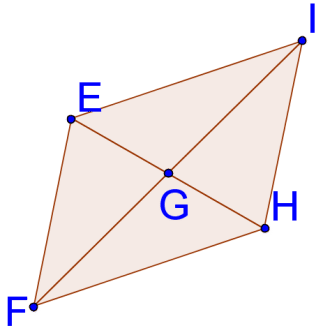
16. Поясніть, чому ААА не є критерієм конгруентності трикутника.
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, натисніть тут.
Додаткові ресурси
Відео: Конгруентні та подібні трикутники - КА
Практика: Конгруентні трикутники