4.11: Теорема третього кута

Last updated
Save as PDF

Page ID: 54751

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Треті кути рівні, якщо інші дві множини є конгруентними.

Якщо два кути в одному трикутнику конгруентні двом кутам в іншому трикутнику, то третя пара кутів також повинна бути конгруентною. Це називається теоремою третього кута.

Якщо\(\angle A\cong \angle D\) і\(\angle B\cong \angle E\), то\(\angle C\cong \angle F\).

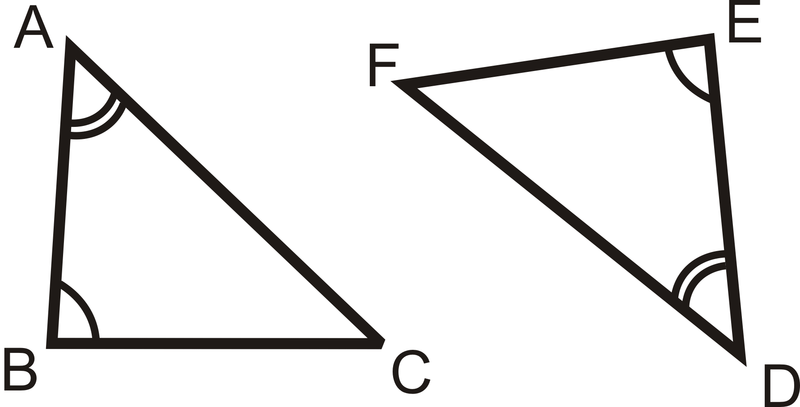
F-д_471д734ФД862 Д213Ф14Б32Д06Ф34ФФ 18Е11324Д937Д1СА29 дек 099C+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Що робити, якщо вам дали\(\Delta FGH\)\(\Delta XYZ\) і вам сказали, що\(\angle F\cong \angle X\) і\(\angle G\cong \angle Y\)? Який висновок ви могли б зробити\(\angle H\) і\(\angle Z\)?

Приклад\(\PageIndex{1}\)

Визначте міру всіх кутів в кожному трикутнику.

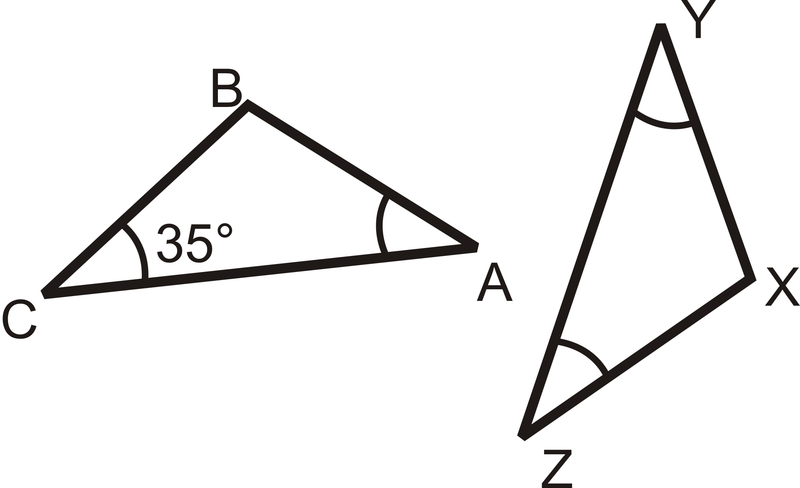
F-D_56Д05С34153466А65АЕ6254 ДБК9Е4Ф76Е75СА6606ФА EBF3975C19E6+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

\(m\angle C=m\angle A=m\angle Y=m\angle Z=35\). За теоремою про суму трикутника\(m\angle B=m\angle X=110\).

Приклад\(\PageIndex{2}\)

Визначте міру всіх кутів в кожному трикутнику.

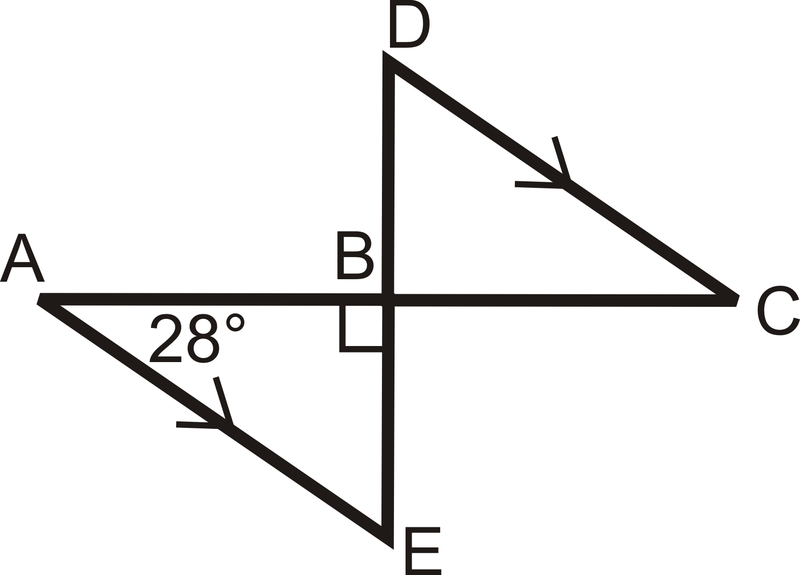
Ф-д_282193С299А005Б0Е5Б8 ААФ ФС431192ДФ 59AD3DE99AC2DF1E6CF46476+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

\(m\angle A=28\),\(m\angle ABE=90\) і за теоремою про суму трикутника,\(m\angle E=62\). \(m\angle D=m\angle E=62\)тому що вони чергуються внутрішні кути, а лінії паралельні. \(m\angle C=m\angle A=28\)тому що вони чергуються внутрішні кути, а лінії паралельні. \(m\angle DBC=m\angle ABE=90\)тому що вони є вертикальними кутами.

Приклад\(\PageIndex{3}\)

Визначте міру відсутніх кутів.

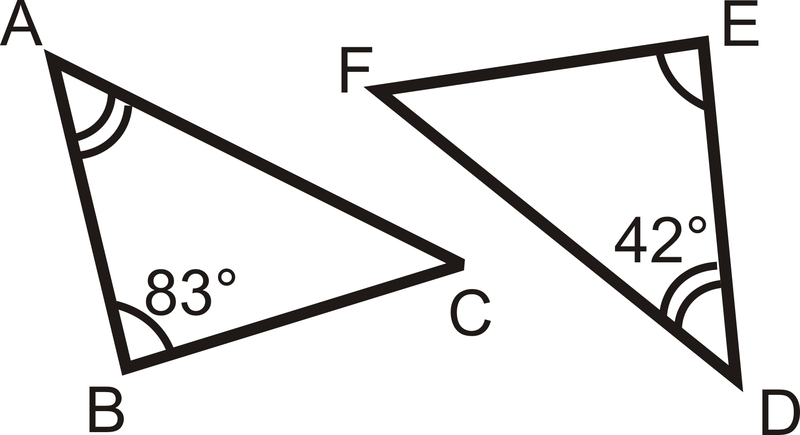
F-D_28FC2A 1 плата 2 ABF 230CFE 9034DC 130E4ЕС09FE93BA86E16490597B79A+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

З теореми третього кута ми знаємо\(\angle C\cong \angle F\). З теореми про суму трикутника ми знаємо, що сума внутрішніх кутів у кожному трикутнику є\(180^{\circ}\).

\(\begin{align*} m\angle A+m\angle B+m\angle C &=180^{\circ} \\ m\angle D+m\angle B+m\angle C=180^{\circ} \\ 42^{\circ}+83^{\circ}+m\angle C &=180^{\circ}\\ m\angle C &=55^{\circ}=m\angle F\end{align*}\)

Приклад\(\PageIndex{4}\)

Поясніть, чому працює теорема третього кута.

Рішення

Теорема третього кута дійсно схожа на продовження теореми про суму трикутника. Після того, як ви знаєте два кути в трикутнику, ви автоматично знаєте третій через теорему про суму трикутника. Це означає, що якщо у вас є два трикутники з двома парами кутів, конгруентних між ними, коли ви використовуєте теорему про суму трикутника на кожному трикутнику, щоб придумати третій кут, ви отримаєте однакову відповідь обидва рази. Тому третя пара кутів також повинна бути конгруентною.

Приклад\(\PageIndex{5}\)

Визначаємо міру всіх кутів в трикутнику:

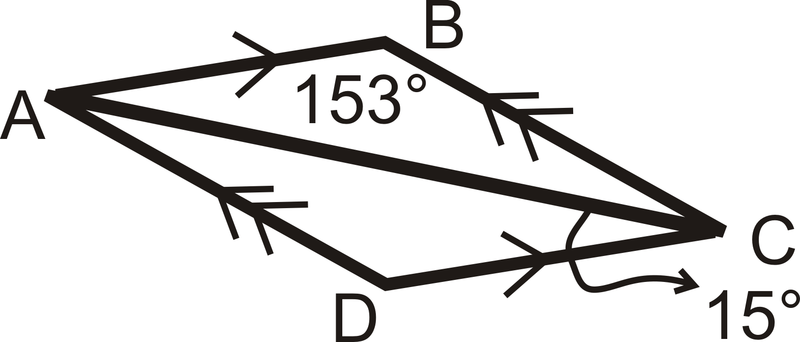
Ф-Д_ДА 675016 ФК 17472 ББ403А2А18997А80С652648Е6Д9Д4ЕЕ078CF90+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

Спочатку ми можемо це побачити\(m\angle DCA=15^{\circ}\). Це означає, що\(m\angle BAC=15^{\circ}\) ще й тому, що вони чергують внутрішні кути. \(m\angle ABC=153^{\circ}\)було дано. Це означає, що теорема про суму трикутника\(m\angle BCA=12^{\circ}\). Це означає, що\(m\angle CAD=12^{\circ}\) ще й тому, що вони чергують внутрішні кути. Нарешті,\(m\angle ADC=153^{\circ}\) за теоремою про суму трикутника.

Рецензія

Визначте міри невідомих кутів.

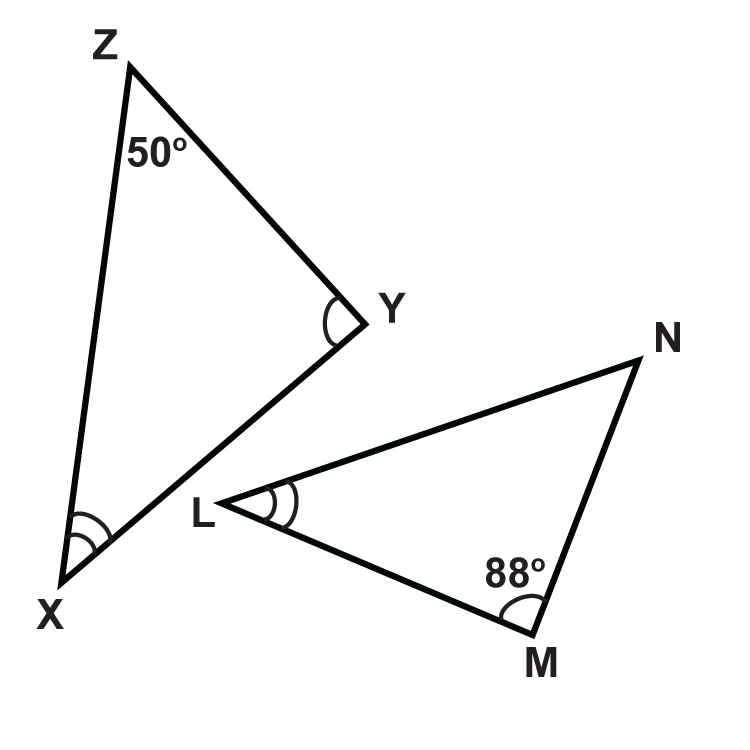
F-D_CF693ЕД 363Ф17Ф9595ФБ7А 76897Е 06181Б3298ДБД21456Д9БК520Б3Б+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

\(\angle Y\)
\(\angle x\)
\(\angle N\)
\(\angle L\)

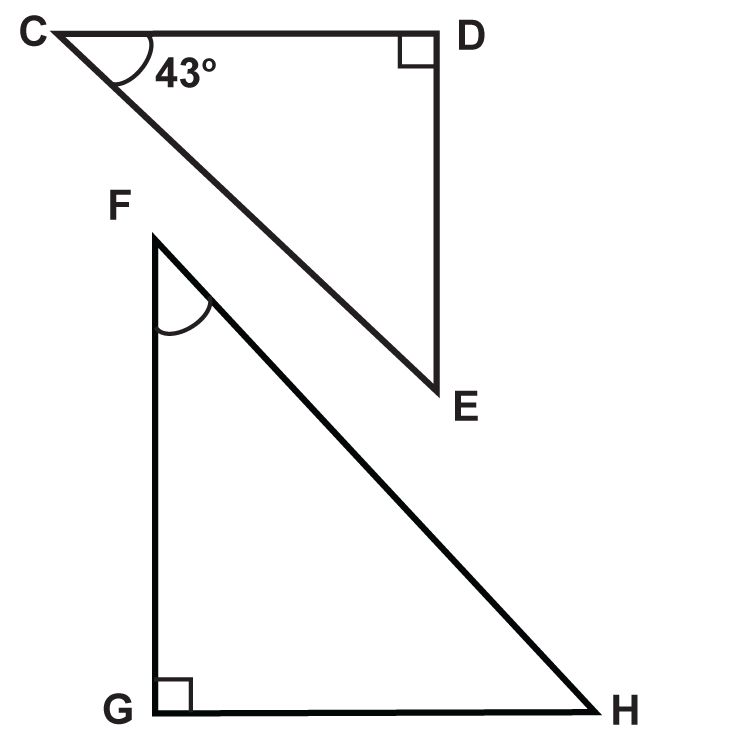
Ф-д_С359Е41КСА 6А5БФ9Б26БК 1974Д60С87А6А7Е8Д84Ф28С68Е39АФ+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

\(\angle E\)
\(\angle F\)
\(\angle H\)

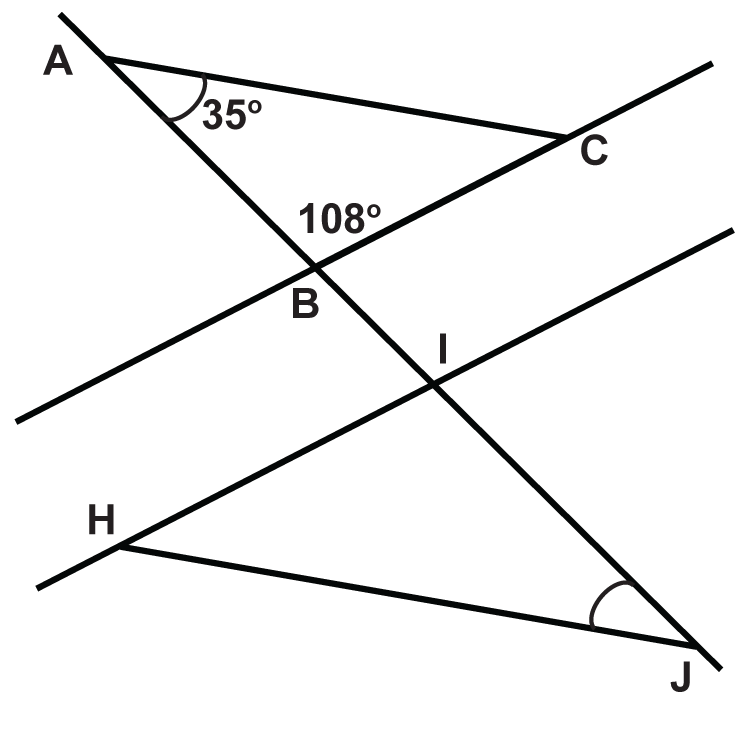
F-д_99224d57d978d8467f1dca05760e7 АФД5022Д151А11Е6Б3Б93Е2А+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Ви можете припустити, що\(\overleftrightarrow{BC}\parallel\overleftrightarrow{HI}\).

\(\angle ACB\)
\(\angle HIJ\)
\(\angle HJI\)
\(\angle IHJ\)

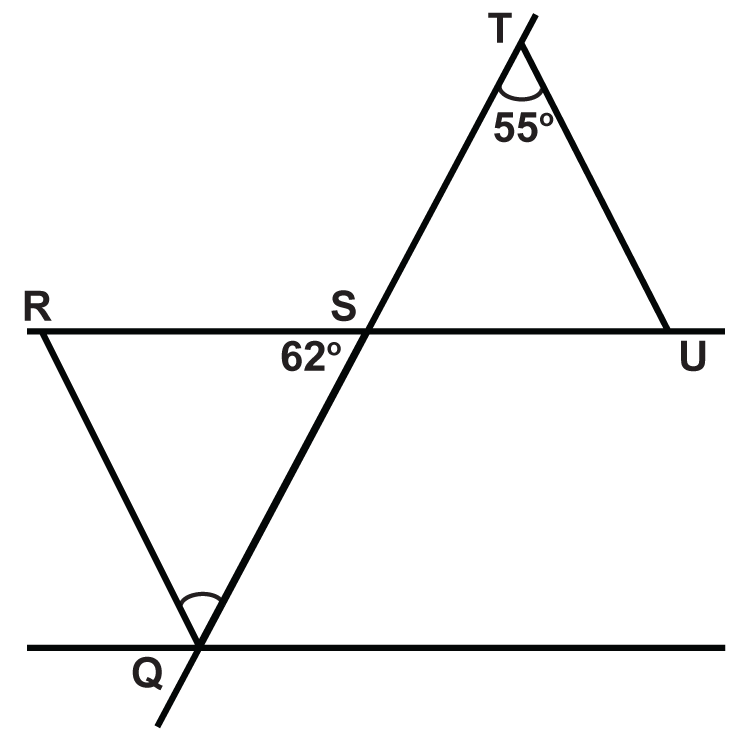
F-д_Д81С43676 ФА4Д30А28 СА49Е8А9АА7Ф9Ф44Ф8Е2Д7Ф66С7941+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

\(\angle RQS\)
\(\angle SRQ\)
\(\angle TSU\)
\(\angle TUS\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.5.

Лексика

Термін	Визначення
Теорема про суму трикутника	*Теорема про суму трикутника* стверджує, що міра трьох внутрішніх кутів будь-якого трикутника буде складатися до\(180^{\circ}\).
Теорема третього кута	Якщо два кути в одному трикутнику конгруентні двом кутам в іншому трикутнику, то третя пара кутів також конгруентна.

Додаткові ресурси

Відео: Принципи теореми третього кута - основні

Види діяльності: Питання обговорення теореми третього кута

Навчальні посібники: Посібник з вивчення конгруентності три

Практика: Теорема третього кута

Реальний світ: Теорема третього кута

\(\angle RQS\)
\(\angle SRQ\)
\(\angle TSU\)
\(\angle TUS\)