4.10: Заяви про конгруентність

Відповідні кути і сторони конгруентних трикутників конгруентні.

При заяві про те, що два трикутника є конгруентними, відповідні частини повинні бути записані в тому ж порядку. Наприклад, якщо ми знаємо, що$\Delta ABC$ і$\Delta LMN$ є конгруентними, то ми знаємо, що:

Малюнок$\PageIndex{1}$

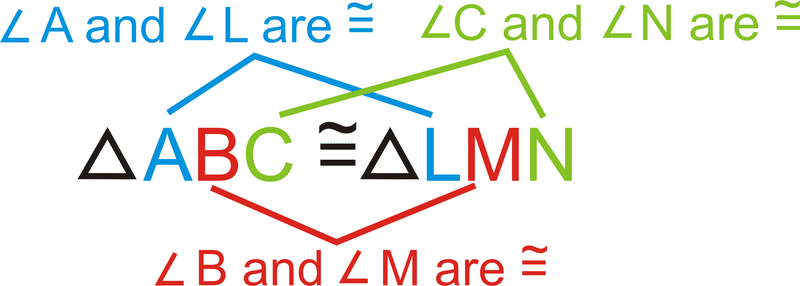
Зверніть увагу, що конгруентні сторони також шикуються всередині заяви про конгруентність.

$\overline{AB} \cong \overline{LM}$,$\overline{BC} \cong \overline{MN}$,$\overline{AC} \cong \overline{LN}$

Ми також можемо написати цю конгруентність заяву п'ять інших способів, поки конгруентні кути збігаються. Наприклад, ми також можемо написати$\Delta ABC\cong \Delta LMN$ як:

$\begin{align*} \Delta ACB\cong \Delta LNM &\qquad& \Delta BCA\cong \Delta MNL &\qquad& \Delta BAC\cong \Delta MLN \\ \Delta CBA\cong \Delta NML &\qquad& \Delta CAB\cong \Delta NLM \end{align*}$

Що робити, якщо вам це сказали$\Delta FGH\cong \Delta XYZ$? Як ви могли б визначити, яка сторона в$\Delta XYZ$ конгруентна$\overline{GH}$ і який кут є конгруентним$\angle F$?

Приклад$\PageIndex{1}$

Якщо$\Delta ABC\cong \Delta DEF$, що ще ви знаєте?

Рішення

З цієї конгруентності ми знаємо, що три пари кутів і три пари сторін є конгруентними.

$\angle A\cong \angle D,\angle B\cong \angle E$,\ кут C\ cong\ кут F\),

$\overline{AB} \cong \overline{DE} , \overline{BC} \cong \overline{EF} , \overline{AC} \cong \overline{DF}$.

Приклад$\PageIndex{2}$

Якщо$\Delta KBP\cong \Delta MRS$, що ще ви знаєте?

Рішення

З цієї конгруентності ми знаємо, що три пари кутів і три пари сторін є конгруентними.

$\angle K\cong \angle M,\:\angle B\cong \angle R,\:\angle P\cong \angle S$,

$\overline{KB} \cong \overline{MR} ,\:\overline{BP} \cong \overline{RS}, \: \overline{KP} \cong \overline{MS}$.

Приклад$\PageIndex{3}$

Напишіть конгруентність для двох трикутників нижче.

Малюнок$\PageIndex{2}$

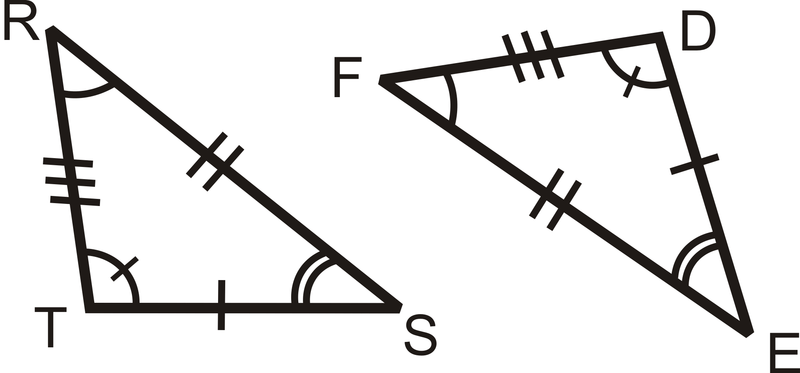
Рішення

Вирівняйте відповідні кути в трикутниках:

$\angle R\cong \angle F,\:\angle S\cong \angle E\:and \angle T\cong \angle D$.

Тому одним з можливих тверджень конгруентності є$\Delta RST\cong \angle FED$

Приклад$\PageIndex{4}$

Якщо$\Delta CAT\cong \Delta DOG$, що ще ви знаєте?

Рішення

З цієї конгруентності ми знаємо, що три пари кутів і три пари сторін є конгруентними.

Малюнок$\PageIndex{3}$

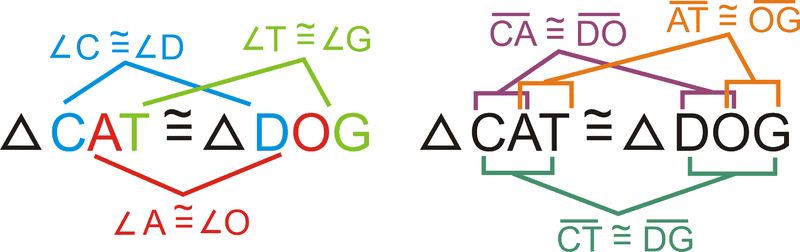
Приклад$\PageIndex{5}$

Якщо$\Delta BUG\cong \Delta ANT$, який кут конгруентний$\angle N$?

Рішення

Оскільки порядок букв у твердженні конгруентності говорить нам, які кути є конгруентними,$\angle N\cong \angle U$ тому що вони є другою з трьох літер.

Рецензія

Для питань 1-4 визначте, чи є трикутники конгруентними, використовуючи визначення конгруентних трикутників. Якщо вони є, напишіть заяву про конгруентність.

1. 

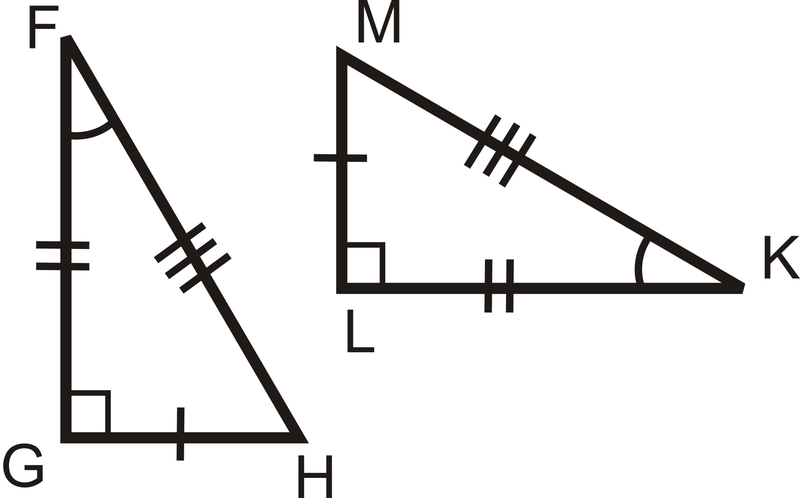
   Малюнок$\PageIndex{4}$

2. 

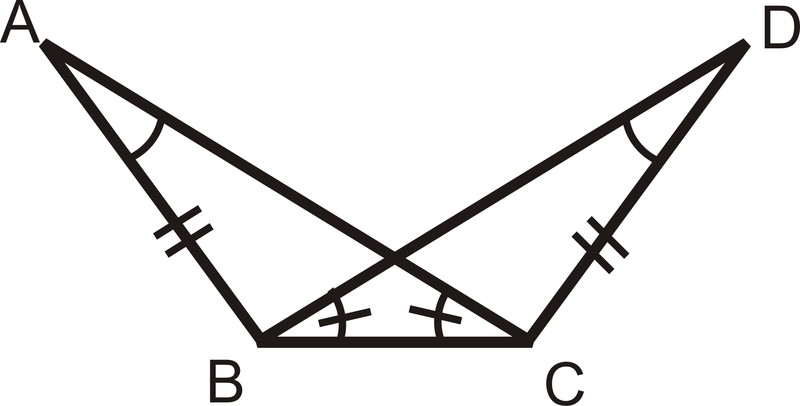
   Малюнок$\PageIndex{5}$

3. 

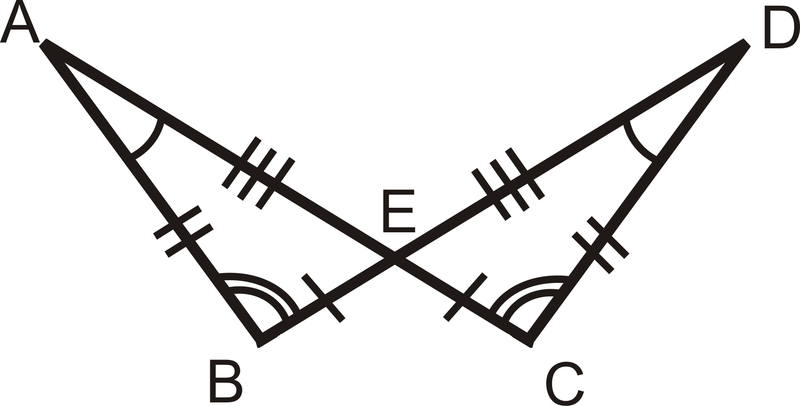
   Малюнок$\PageIndex{6}$

4. 

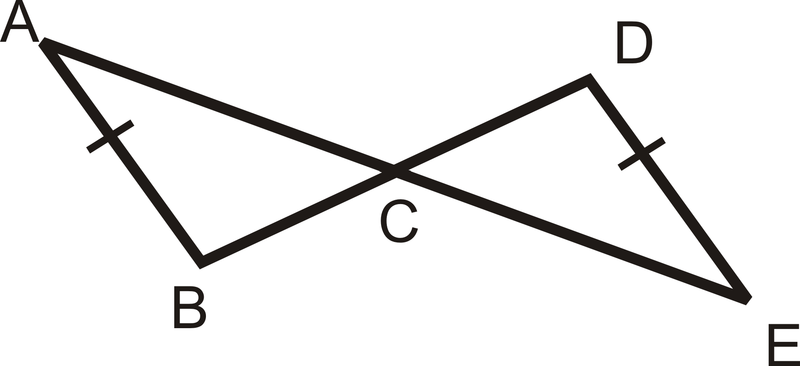
   Малюнок$\PageIndex{7}$

5. Припустимо, що два трикутника нижче є конгруентними. Напишіть конгруентність для цих трикутників.

   

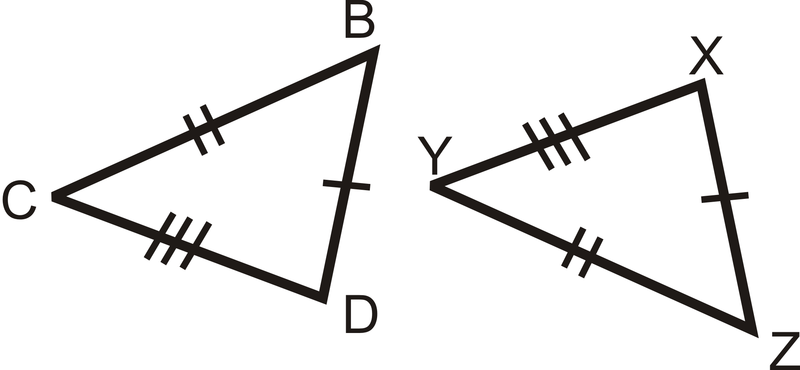
   Малюнок$\PageIndex{8}$

6. Поясніть, як ми знаємо, що якщо два трикутники конгруентні, то$\angle B\cong \angle Z$.
7. Якщо$\Delta TBS\cong \Delta FAM$, що ще ви знаєте?
8. Якщо$\Delta PAM\cong \Delta STE$, що ще ви знаєте?
9. Якщо$\Delta INT\cong \Delta WEB$, що ще ви знаєте?
10. Якщо$\Delta ADG\cong \Delta BCE$, який кут конгруентний$\angle G$?

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.4.

Ресурси

Додаткові ресурси

Відео: Вступ до конгруентних трикутників

Діяльність: Конгруентність Заяви Обговорення Питання

Навчальні посібники: Посібник з вивчення конгруентності три

Практика: Заяви про конгруентність

Реальний світ: Конгруентні заяви