4.9: КПВТК

Last updated
Save as PDF

Page ID: 54804

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Сторони і кути конгруентних трикутників мають однакову міру.

Конгруентні трикутники

Дві фігури конгруентні, якщо вони мають абсолютно однаковий розмір і форму. Якщо два трикутника конгруентні, вони матимуть абсолютно однакові три сторони і точно такі ж три кути. Іншими словами, два трикутника є конгруентними, якщо ви можете повернути, перевернути та/або ковзати один так, щоб він точно вписувався на інший.

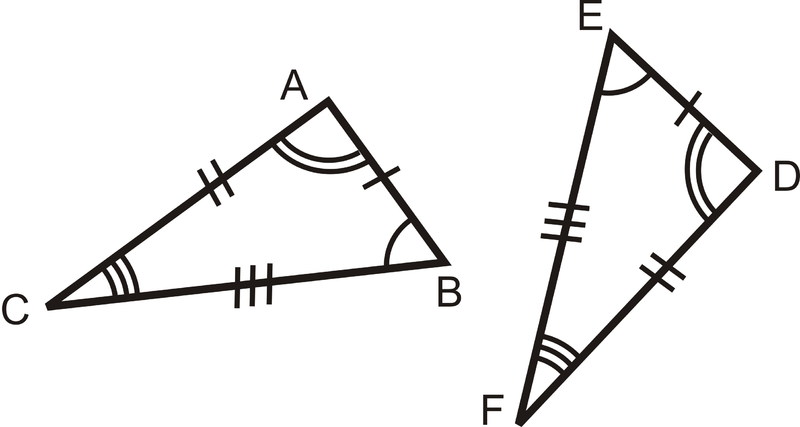
F-д_Ф 6068Ф8А2Д070Б8С8С894C44 АДЕ 33Ф50СЕ 656Ф6933 АЭС 45A44A4A68E58+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

\(\Delta ABC\)і\(\Delta DEF\) є конгруентними, тому що

\(\begin{align*}\overline{AB}\cong DE &\qquad& \angle A\cong \angle D \\ \overline{BC}\cong EF\overline{AB}&\:and\:& \angle B\cong \angle E \\ \overline{AC}\cong \overline{DF} &\qquad& \angle C\cong \angle F \end{align*}\)

Зверніть увагу, що коли два трикутники конгруентні, їх три пари відповідних кутів і їх три пари відповідних сторін є конгруентними.

Посилаючись на відповідні конгруентні частини конгруентних трикутників, ви можете використовувати фразу C, що відповідають P частини C congruent T трикутники є C congruent, або її абревіатура CPCTC.

Що робити, якщо вам дали два трикутники з усіма мірами кута і всіма боковими довжинами позначені? Як ви могли зрозуміти, чи два трикутники були конгруентними?

Приклад\(\PageIndex{1}\)

Визначте, чи є трикутники конгруентними, використовуючи визначення конгруентних трикутників.

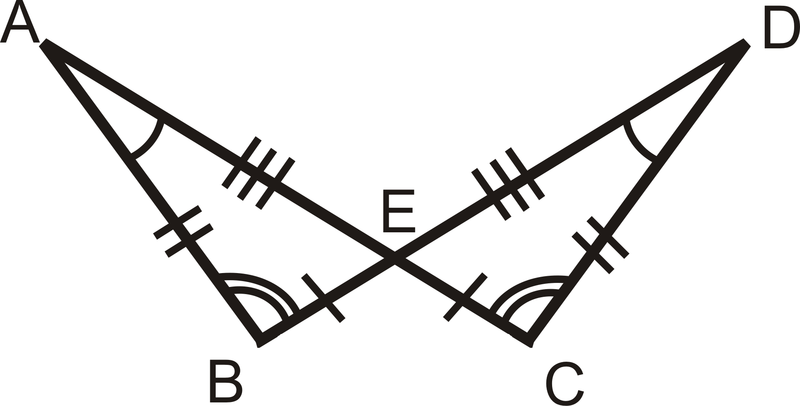
F-D_A242056D69C2F635D8B4421352954D13716F8B3D86A94А04ЕКА 28 постійного струму+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Рішення

Ми бачимо з маркування\(\angle B\cong \angle C\), що, і\(\angle AEB\cong \angle DEC\) тому\(\angle A\cong \angle D\), що вони вертикальні кути. Крім того, ми знаємо\(\overline{BA}\cong \overline{CD}\), що\(\overline{EA}\cong \overline{ED}\), і\(\overline{BE}\cong \overline{CE}\). Оскільки три пари сторін і три пари кутів є конгруентними, і вони є відповідними частинами, це означає, що два трикутники є конгруентними.

Приклад\(\PageIndex{2}\)

Визначте, чи є трикутники конгруентними, використовуючи визначення конгруентних трикутників.

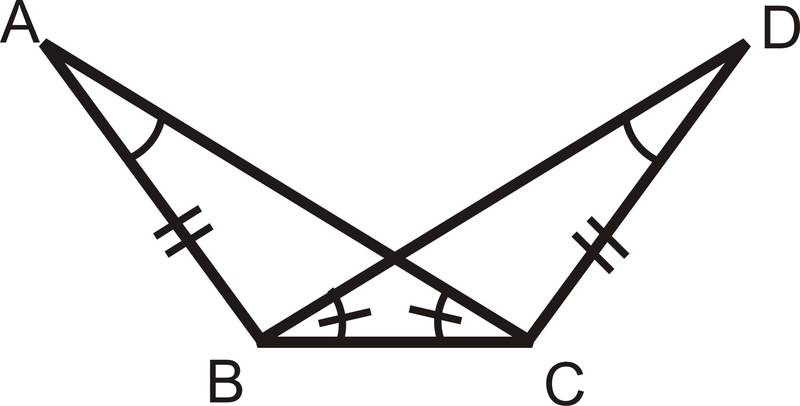
F-д_2С72БКА 826Ф55Б50536343Б9А1ФСБ 9Д8370014 ББ009Б6Д338167CD8A+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Рішення

Хоча є конгруентні відповідні частини, є лише дві пари конгруентних сторін, позначені та спільна сторона. Не знаючи, чи є третя пара сторін конгруентною, ми не можемо сказати, чи є трикутники конгруентними, використовуючи визначення конгруентних трикутників. Зверніть увагу, це не означає, що трикутники не є конгруентними, це просто означає, що нам потрібно більше інформації, щоб сказати, що вони конгруентні, використовуючи визначення конгруентних трикутників (конгруентні трикутники мають три пари конгруентних кутів і три пари конгруентних сторін).

Приклад\(\PageIndex{3}\)

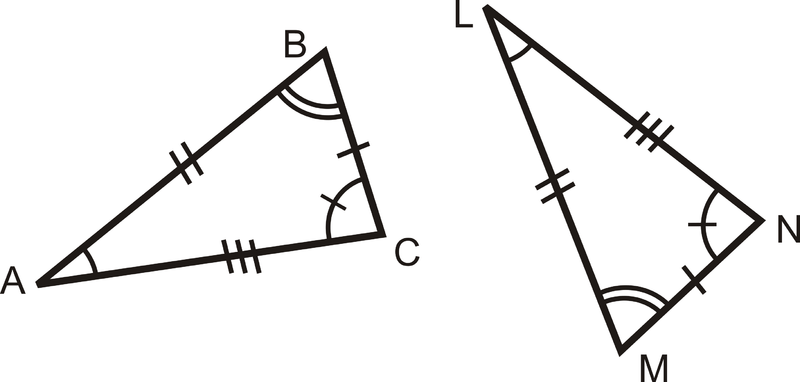
Чи є два трикутника нижче конгруентних?

F-д_д29а 6ДДА 47853Д8795990А176Ф6А3792 АБ294А8Б2391Д2Б76С1ББ0С4+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Рішення

Щоб визначити, чи є трикутники конгруентними, зіставте сторони з однаковою кількістю міток tic:\(\overline{BC}\cong \overline{MN}\),\(\overline{AB}\cong \overline{LM}\),\(\overline{AC}\cong \overline{LN}\).

Далі зіставляємо кути з такою ж розміткою:

\(\angle A\cong \angle L\),\(\angle B\cong \angle M\), і\(\angle C\cong \angle N\).

Нарешті, нам потрібно переконатися, що це відповідні частини. Для цього перевірте, чи є конгруентні кути протилежними конгруентними сторонами. Тут\(\angle A\), навпаки\(\overline{BC}\) і\(\angle L\) навпаки\(\overline{MN}\). Тому що\(\angle A\cong \angle L\) і\(\overline{BC}\cong \overline{MN}\), вони відповідні. Роблячи цю перевірку для інших сторін та кутів, ми бачимо, що все збігається, а два трикутники конгруентні.

Приклад\(\PageIndex{4}\)

Якщо всі три пари кутів для двох заданих трикутників є конгруентними, це означає, що трикутники є конгруентними?

Рішення

Не знаючи нічого про довжину сторін, ви не можете сказати, чи є два трикутники конгруентними. Два трикутника, описані вище, можуть бути конгруентними, але нам знадобиться більше інформації, щоб знати напевно.

Приклад\(\PageIndex{5}\)

Визначте, чи є трикутники конгруентними, використовуючи визначення конгруентних трикутників.

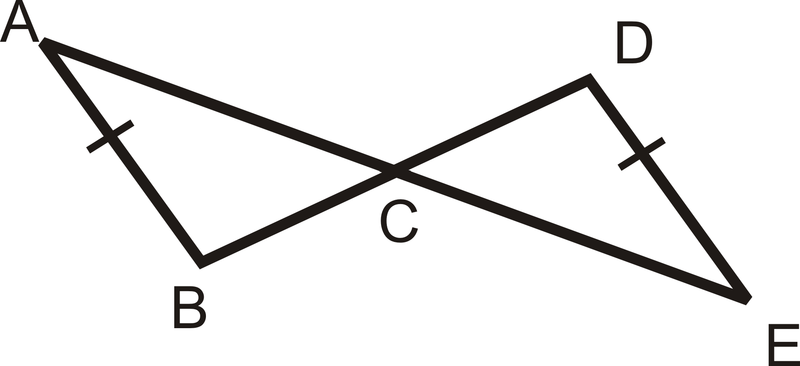
F-д_а698 плойка 48Ф3БФ 5Ф22Б479400 CCCC53A28971 Ф6 Ф8 ЕФ8ЕФ03498D5A+зображення_крихіткий+зображення_крихітка_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

З міток тик ми бачимо, що\(\overline{AB}\cong \overline{DE}\). Ми також знаємо це\(\angle ACB\cong \angle ECD\) тому, що вони є вертикальними кутами. Однак цієї інформації недостатньо, щоб знати, чи є трикутники конгруентними.

Рецензія

Наступні ілюстрації показують дві паралельні лінії, вирізані поперечним (Ви можете припустити, що навіть якщо лінії не позначені паралельно, дві лінії, які виглядають паралельно, насправді є). Чи трикутники, утворені ними, остаточно конгруентні?

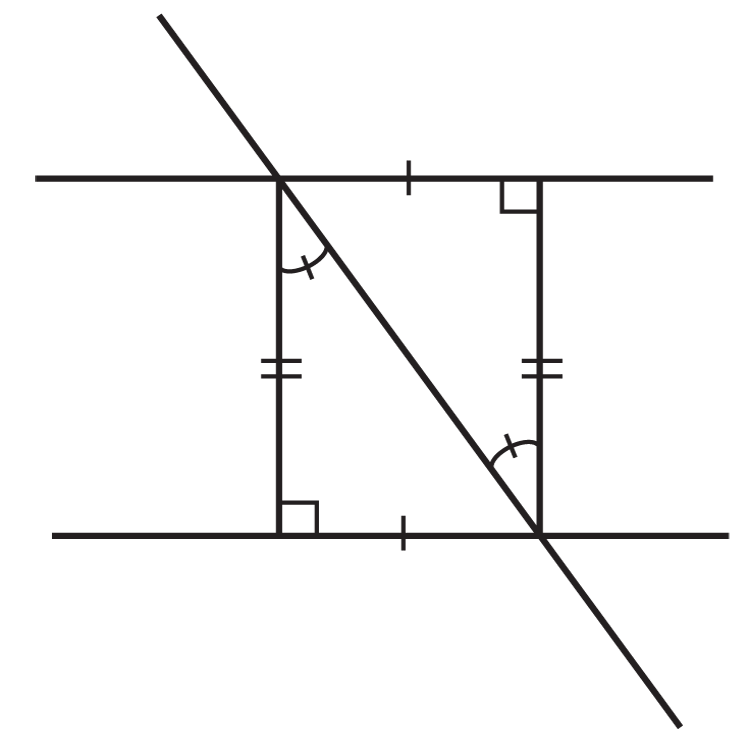
Малюнок\(\PageIndex{6}\)
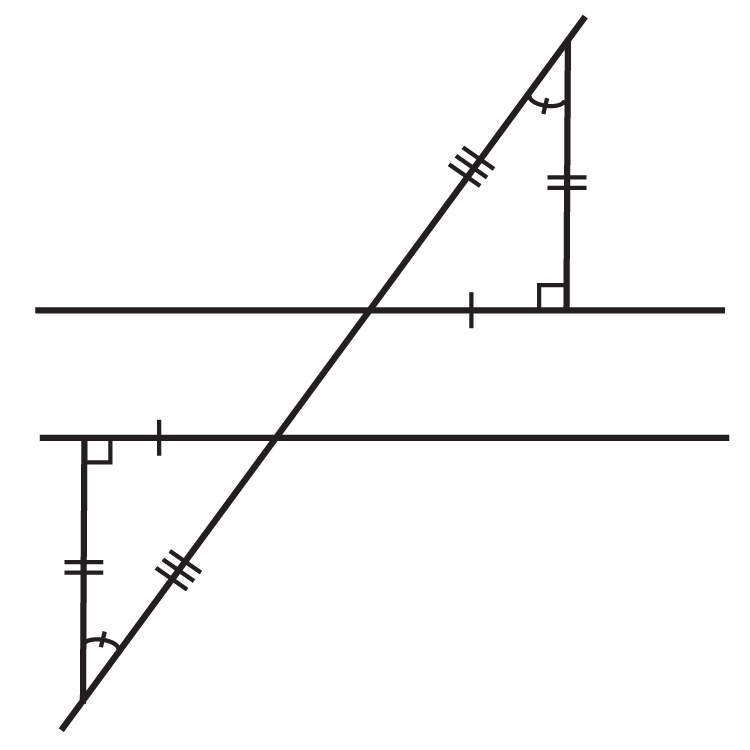
Малюнок\(\PageIndex{7}\)
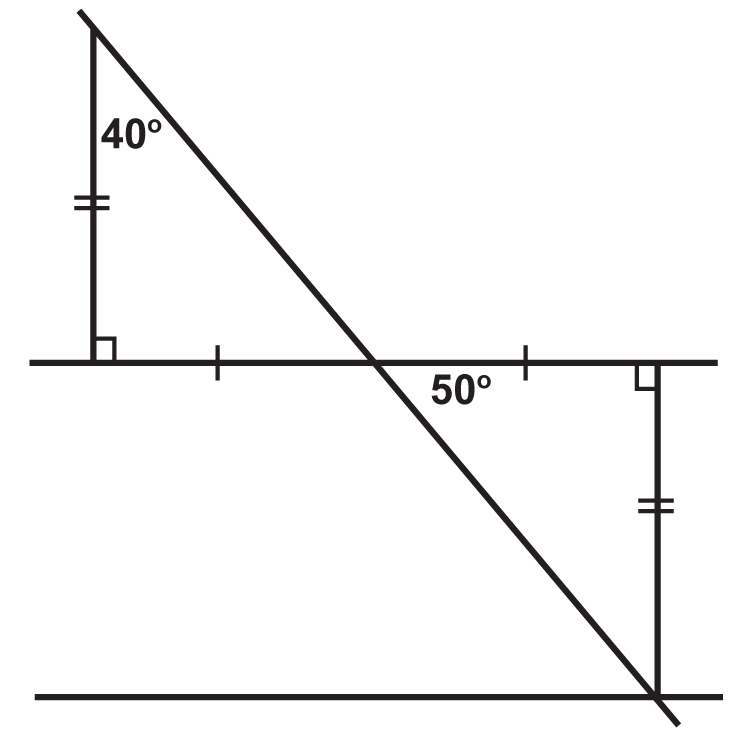
Малюнок\(\PageIndex{8}\)
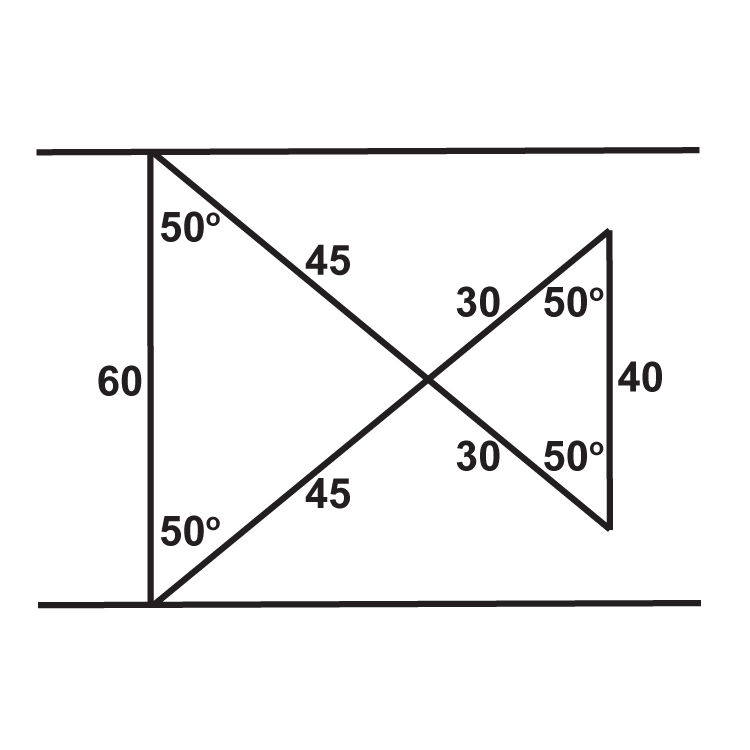
Малюнок\(\PageIndex{9}\)
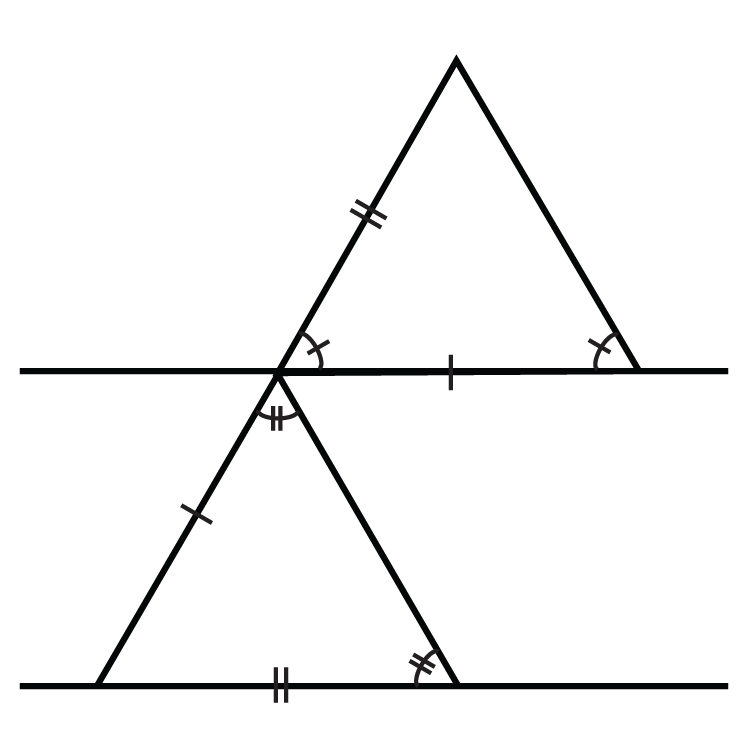
Малюнок\(\PageIndex{10}\)

Виходячи з наступних деталей, трикутники остаточно конгруентні?

Обидва трикутника - це прямі трикутники, в яких вимірюється один кут\(55^{\circ}\). Всі відповідні їм сторони є конгруентними.
Обидва трикутника - це рівнокутні трикутники.
Обидва трикутника є рівносторонніми трикутниками. Всі сторони мають довжину 5 дюймів.
Обидва трикутника є тупими трикутниками, в яких вимірюється один кут\(35^{\circ}\). Дві відповідні їм сторони є конгруентними.
Обидва трикутника є тупими трикутниками, в яких два їх кути вимірюють\(40^{\circ}\) і\(20^{\circ}\). Всі відповідні їм сторони є конгруентними.
Обидва трикутника - це рівнобедрені трикутники, в яких вимірюється один кут\(15^{\circ}\).
Обидва трикутника є рівнобедреними трикутниками з двома рівними кутами\(55^{\circ}\). Всі відповідні сторони є конгруентними.
Обидва трикутника - це гострі трикутники, в яких два їх кути вимірюють\(40^{\circ}\) і\(80^{\circ}\). Всі відповідні їм сторони є конгруентними.
Обидва трикутника - це гострі трикутники, в яких вимірюється один кут\(60^{\circ}\). Дві відповідні їм сторони є конгруентними.
Обидва трикутника є рівносторонніми трикутниками.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.3.

Ресурси

Лексика

Термін	Визначення
Теорема третього кута	Якщо два кути в одному трикутнику конгруентні двом кутам в іншому трикутнику, то третя пара кутів також конгруентна.

Додаткові ресурси

Інтерактивний елемент

Відео: Конгруентні та подібні трикутники

Діяльність: Конгруентні трикутники Дискусійні питання

Навчальні посібники: Посібник з вивчення конгруентності три

Практика: CPCTC

Реальний світ: Конгруентні трикутники