4.7: Площа трикутника

Last updated
Save as PDF

Page ID: 54893

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Террі має два квитки на наступну домашню гру своєї улюбленої футбольної команди коледжу, тому він планує взяти свого молодшого брата з собою на гру. Террі хоче зробити два вимпела для гри, тому він купує шматок матеріалу у формі прямокутника з основою 18 дюймів і висотою 12 дюймів. Террі планує розділити матеріал на два трикутника. Як Террі може з'ясувати площу кожного з трикутників, які будуть вирізані з матеріалу для його вимпелів?

У цій концепції ви навчитеся знаходити площі трикутників, заданих підставою і висотою.

Пошук площі трикутника

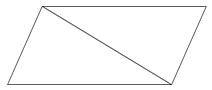
Трикутники не є паралелограмами, оскільки вони мають лише три сторони, але вони пов'язані з паралелограмами. Погляньте на паралелограм нижче і подивіться, чи зможете ви розібратися в підключенні.

Якщо придивитися уважно, то помітите, що паралелограм можна розділити на два трикутника.

Прямокутник - це тип паралелограма з чотирма прямими кутами. Ви також можете розділити прямокутник на два трикутника.

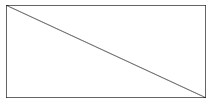
Зверніть увагу, що прямокутник розділений на два прямокутні трикутники, трикутники, що містять прямий кут.

Квадрат - це тип прямокутника з чотирма рівними сторонами і чотирма прямими кутами. Квадрат також можна розділити на два прямих трикутника.

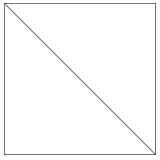
Якщо паралелограм можна розділити на два трикутника, то площа трикутника дорівнює половині площі паралелограма.

Давайте розглянемо, як це працює.

Яка площа цього паралелограма?

Щоб знайти площу паралелограма, помножте підставу на висоту.

\(\begin{align*} A &=bh\\ A&=2(5)\\ A&=10 sq.\: inches.\end{align*} \)

Паралелограм можна розділити на два трикутника.

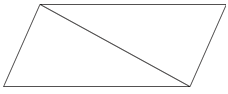
Якщо розділити площу паралелограма навпіл, це дасть вам площу одного з трикутників.

\(10\div 2=5 sq.\: inches\)

Виходячи з цієї інформації, можна написати наступну формулу знаходження площі трикутника.

\(A=\dfrac{1}{2}bh\)

Трикутник - це половина паралелограма, тому формула для паралелограма, помноженого на половину, є формулою знаходження площі трикутника.

Приклад\(\PageIndex{1}\)

Раніше вам давали проблему з приводу Террі і його спортивних вимпелів.

Террі завжди був футбольним вболівальником Gator, тому він схвильований відвідуванням однієї з домашніх ігор команди. Він придбав матеріал для виготовлення двох вимпелів для гри. Матеріал має форму прямокутника, і Террі планує розділити його на два трикутника для вимпелів. Матеріал має 38-дюймову основу і висоту 30 дюймів. Террі хоче дізнатися розмір двох трикутників після того, як він розрізає матеріал. Як Террі може з'ясувати площу кожного з трикутників, які будуть утворювати його вимпели?

Рішення

Ось подивіться на шматок матеріалу.

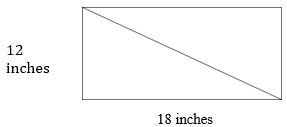
По-перше, нагадаємо, що площа прямокутника дорівнює базовій висоті, а трикутник - половина площі прямокутника.

\(\begin{align*}Base\times Height &=Area \:of \:a\: Rectangle \\ 18\times 12&=216 \\ &=216 \: square \:inches \end{align*}\)

Далі підставляємо значення площі прямокутника (або висоти основи\ times) у формулу площі трикутника.

\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(216) \end{align*}\)

Потім вирішіть рівняння.

\(\begin{align*}A&=\dfrac{1}{2}(216) \\ A&=108\: square\: inches \end{align*}\)

Відповідь - кожен з трикутників матиме площу 108 квадратних дюймів.

Приклад\(\PageIndex{2}\)

Знайдіть площу трикутника з основою 6 футів і висотою 5 футів.

Рішення

Спочатку підставляємо значення основи та висоти у формулу площі трикутника.

\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=12(6)(5) \end{align*}\)

Далі вирішуємо рівняння.

\(\begin{align*}A&=12(30) \\ A&=15\: square feet \end{align*}\)

Відповідь - 15 квадратних футів.

Приклад\(\PageIndex{3}\)

Використовуючи площу наступного паралелограма, знайдіть площу одного з трикутників всередині паралелограма.

Рішення

Площа прямокутника 12 кв. дюймів

Далі підставляємо значення площі для основи та висоти у формулу площі трикутника.

\(\begin{align*}A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(12) \end{align*}\)

Потім вирішіть рівняння.

\(\begin{align*}A&=\dfrac{1}{2}(12) \\ A&=6\: square \:inches \end{align*}\)

Відповідь - 6 квадратних дюймів.

Приклад\(\PageIndex{4}\)

Рішення

Площа паралелограма становить 24 кв. футів

По-перше, нагадаємо, що площа паралелограма дорівнює базовій висоті, а трикутник - половина площі паралелограма.

Далі підставляємо значення площі для основи та висоти у формулу площі трикутника.

\(\begin{align*} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(24) \end{align*}\)

Потім вирішіть рівняння.

\(\begin{align*} A&=\dfrac{1}{2}(24) \\ A&=12\: square\: feet \end{align*}\)

Відповідь - 12 квадратних футів.

Приклад\(\PageIndex{5}\)

Рішення

Площа паралелограма 18 кв. футів

Спочатку підставляємо значення площі для основи та висоти у формулу площі трикутника.

\(\begin{align*} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(18)\end{align*}\)

Потім вирішіть рівняння.

\(\begin{align*} A&=\dfrac{1}{2}(18) \\ A&=9\: square\: feet \end{align*}\)

Відповідь - 9 квадратних футів.

Рецензія

Знайти площу кожного трикутника за даними наступних вимірів.

Малюнок\(\PageIndex{6}\)

База = 10 дюймів, Висота = 4 дюйма

Малюнок\(\PageIndex{7}\)

База = 16 метрів, Висота = 10 метрів
Малюнок\(\PageIndex{8}\)

База = 8 дюймів, Висота = 6,5 дюйма

Малюнок\(\PageIndex{9}\)

Підстава = 10 см, Висота = 7 см

Малюнок\(\PageIndex{10}\)

База = 5 футів, висота = 8,5 футів

Знайдіть площу кожного трикутника з урахуванням підстави і висоти.

База = 4 дюйми, Висота = 5 дюйм
База = 6 дюйм, Висота = 4 в
База = 8 футів, Висота = 7 футів
База = 10 метрів, Висота = 8 метрів
База = 10 метрів, Висота = 5 метрів
База = 12 футів, висота = 14 футів
База = 11 футів, висота = 6 футів
База = 14 дюймів, Висота = 8 дюймів
База = 22 фути, висота = 19 футів
Підстава = 30 см, Висота = 28 см
База = 18 дюймів, висота = 16 дюймів
База = 13 метрів, Висота = 10 метрів
База = 18 метрів, Висота = 5,5 метрів
База = 12,5 футів, Висота = 2,5 футів
База = 13,75 дюйма, висота = 1,5 дюйма

Огляд (Відповіді)

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.3.

Ресурси

Лексика

Термін	Визначення
Паралелограм	Паралелограм - це чотирикутник з двома парами паралельних сторін.
Прямокутник	Прямокутник - це чотирикутник з чотирма прямими кутами.
Квадрат	Квадрат - це багатокутник з чотирма конгруентними сторонами і чотирма прямими кутами.

Додаткові ресурси

Інтерактивний елемент

Відео: Площа трикутника (цілі числа)

Практика: Площа трикутника

Реальний світ: Побудова трикутників