Skip to main content
LibreTexts - Ukrayinska

4.6: Площа та периметр трикутників

  1. Last updated
  2. Save as PDF
  • Page ID
    54739

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Площа дорівнює половині підстави на висоту, тоді як периметр - сума сторін.

    Формула площі трикутника дорівнює половині площі паралелограма.

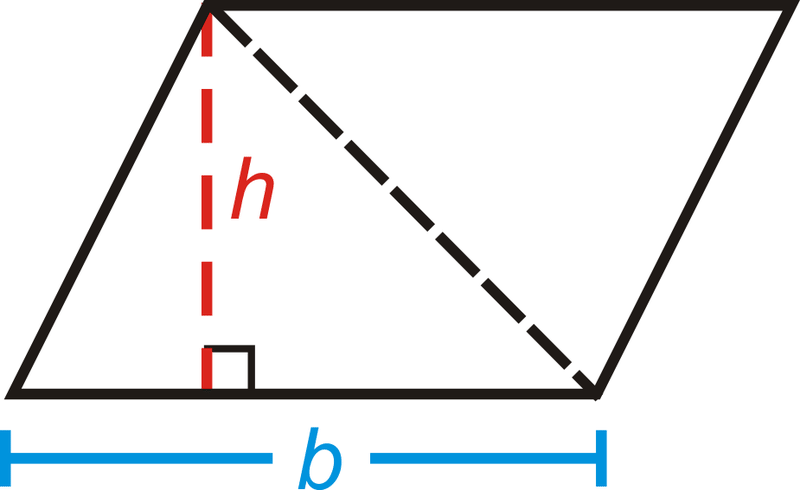
    F-д_4c0c681521c5908019784C1ФБА 3d1c36c4afd60221641d471444E18+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Площа трикутника:\(A=\dfrac{1}{2} bh\) або\(A=\dfrac{bh}{2}\).

    Ф-д_909ЕК 4625918D0ФК 0ДФД 6820Б19940БА1Д7Ф9794А9Б6АФ39АБ0+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Що робити, якщо вам дали трикутник і розмір його підстави і висоту? Як ви могли знайти загальну відстань навколо трикутника та кількість місця, який він займає?

    Для прикладів 1 і 2 використовуйте наступний трикутник.

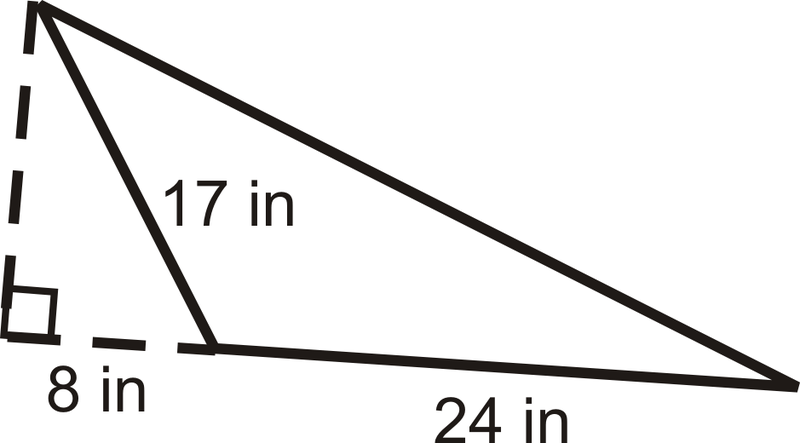
    F-D_433АК 41Е518719Б0С01Б5Б5БД620222С8574946А1А1Ф3FF2651E2E4+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{3}\)

    Приклад\(\PageIndex{1}\)

    Знайдіть висоту трикутника.

    Рішення

    Використовуйте теорему Піфагора, щоб знайти висоту.

    \(\begin{align*} 8^2+h^2 &=17^2 \\ h^2 &=225\\ h &=15 in \end{align*} \)

    Приклад\(\PageIndex{2}\)

    Знайдіть периметр.

    Рішення

    Нам потрібно знайти гіпотенузу. Знову скористайтеся теоремою Піфагора.

    \(\begin{align*} (8+24)^2+15^2 &=h^2 \\ h^2 &=1249 \\ h &\approx 35.3 in \end{align*}\)

    Периметр - це\(24+35.3+17\approx 76.3\: in\).

    Приклад\(\PageIndex{3}\)

    Знайдіть площу трикутника.

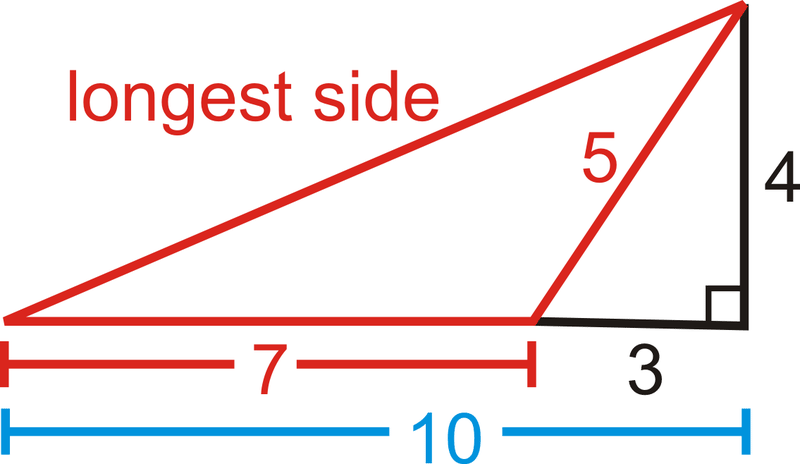
    F-д_4 ДДС6462941435 Дек 5С611Б3571Ф22С6Д49Ф5Ф8КА8Ф2Е56С41C0E8+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{4}\)

    Рішення

    Щоб знайти площу, нам потрібно знайти висоту трикутника. Наведено дві сторони малого прямокутного трикутника, де гіпотенуза також є короткою стороною тупого трикутника.

    \(\begin{align*} 3^2+h^2&=5^2 \\ 9+h^2&=25 \\ h^2&=16 \\h &=4 \\ A&=\dfrac{1}{2}(4)(7)=14 \: units^2 \end{align*}\)

    Приклад\(\PageIndex{4}\)

    Знайдіть периметр трикутника в прикладі 3.

    Рішення

    Щоб знайти периметр, нам потрібно знайти найдовшу сторону тупого трикутника. Якби ми використовували чорні лінії на малюнку, ми побачили б, що найдовшою стороною є також гіпотенуза прямокутного трикутника з катетами 4 і 10.

    \(\begin{align*} 4^2+10^2&=c^2 \\ 16+100&=c^2 \\ c &=\sqrt{116}\approx 10.77 \end{align*} \)

    Периметр -\(7+5+10.77\approx 22.77\) одиниці

    Приклад\(\PageIndex{5}\)

    Знайти площу трикутника з основою довжини\(28 \: cm\) і висоти\(15\: cm\).

    Рішення

    Площа є\(dfrac{1}{2}(28)(15)=210\: cm^2\).

    Рецензія

    Використовуйте трикутник, щоб відповісти на наступні питання.

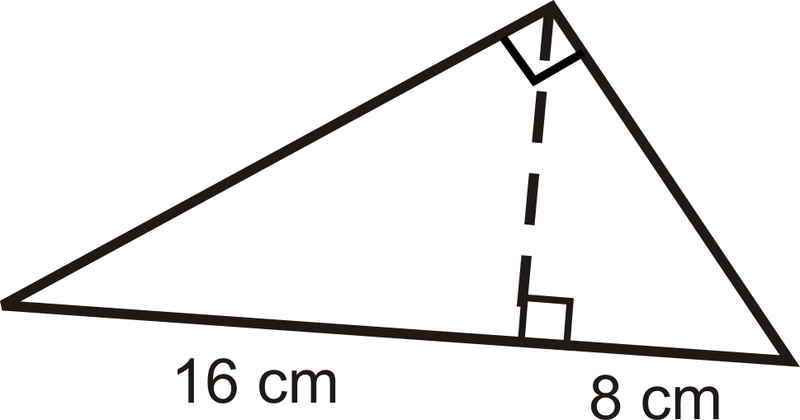
    F-D_B00417194F7CF82E2346b42062316704C5870 Б8293377A9218E2+зображення_крихіткий+зображення_крихітковий_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)
    1. Знайдіть висоту трикутника, використовуючи середнє геометричне.
    2. Знайдіть периметр.
    3. Знайдіть місцевість.

    Знайдіть площу наступної форми.

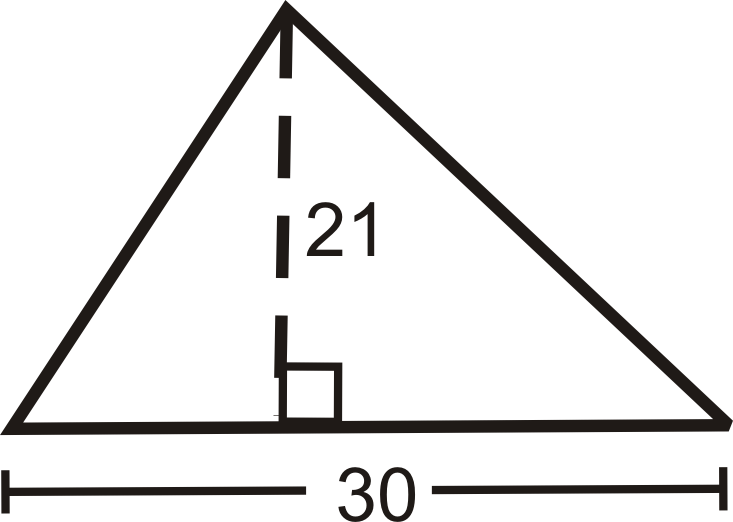
    1. F-д_30БКК 55Е 0170103930D479Ф168441ЕБ89Д69А1Д6642Ф65А0С7Е6805+зображення_крихіткий+зображення_крихіткий_png
      Малюнок\(\PageIndex{6}\)
    2. Яка висота трикутника з площею\(144\: m^2\) і основою\(24\: m\)?

    У питаннях 6-11 ми виведемо формулу для площі рівностороннього трикутника.

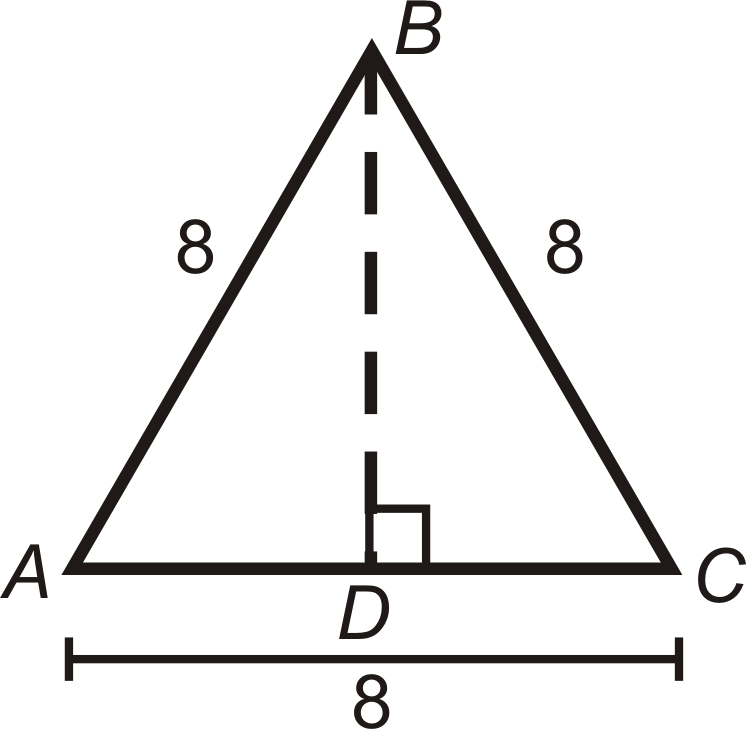
    F-D_10415D49F9724 FA6930A плашка D628 АД 7883728ЕД 212373А3А 3Ф7 CFDB33C+зображення_крихіткий+зображення_крихіткий.png
    Малюнок\(\PageIndex{7}\)
    1. Що це за трикутник\(\Delta ABD\)? Знайти\(AD\) і\(BD\).
    2. Знайдіть площу\(\Delta ABC\).
    3. Якщо кожна сторона є\(x\), що таке\(AD\) і\(BD\)?
    4. Якщо кожна сторона є\(x\), знайдіть площу\(\Delta ABC\).
    5. Використовуючи вашу формулу з #9, знайдіть площу рівностороннього трикутника з 12-дюймовими сторонами.
    6. Використовуючи вашу формулу з #9, знайдіть площу рівностороннього трикутника з 5-дюймовими сторонами.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.3.

    Лексика

    Термін Визначення
    Площа Площа - простір в межах периметра двомірної фігури.
    Периметр Периметр - це відстань навколо двомірної фігури.
    Перпендикуляр Перпендикулярні лінії - це лінії, які перетинаються під кутом 90. Твір ухилів двох перпендикулярних ліній дорівнює -1.
    Прямий кут Прямим кутом вважається кут, рівний 90 градусам.
    Правий трикутник Прямокутний трикутник - це трикутник з одним кутом 90 градусів.
    Площа паралелограма Площа паралелограма дорівнює підстави, помноженої на висоту:\(A = bh\). Висота паралелограма завжди перпендикулярна підставі (сторони - це не висота).
    Площа трикутника Площа трикутника дорівнює половині площі паралелограма. Звідси і формула:\(A=\dfrac{1}{2} bh\) або\(A=\dfrac{bh}{2}\).

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Площа трикутника (цілі числа)

    Діяльність: Площа та периметр трикутників Питання обговорення

    Навчальні посібники: Трикутники та чотирикутники Навчальний посібник

    Практика: Площа та периметр трикутників

    Реальний світ: Периметр