4.5: Рівносторонні трикутники
- Page ID
- 54846
Властивості трикутників з трьома рівними сторонами.
Теорема про рівносторонній трикутник: Всі рівносторонні трикутники також рівнокутні. Крім того, всі рівнокутні трикутники також рівносторонні.
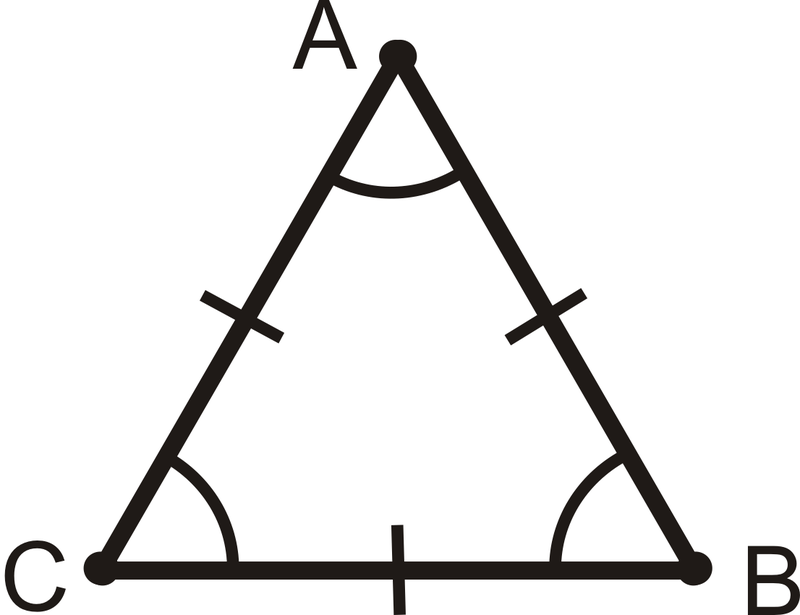
Якщо\(\overline{AB}\cong \overline{BC}\cong \overline{AC}\), то\(\angle A\cong \angle B\cong \angle C\). І навпаки, якщо\(\angle A\cong \angle B\cong \angle C\), то\(\overline{AB}\cong \overline{BC}\cong \overline{AC}\).
Що робити, якщо вам подарували рівносторонній трикутник і сказали, що його сторони вимірюють\(x\) \(y\), і 8? Що ви могли б зробити висновок про\(x\) і\(y\)?
Приклад\(\PageIndex{1}\)
Заповніть доказ:
Дано: Рівносторонній\(\Delta RST\) з
\(\overline{RT}\cong \overline{ST}\cong \overline{RS}\)
Доведіть:\(\Delta RST\) рівнокутна
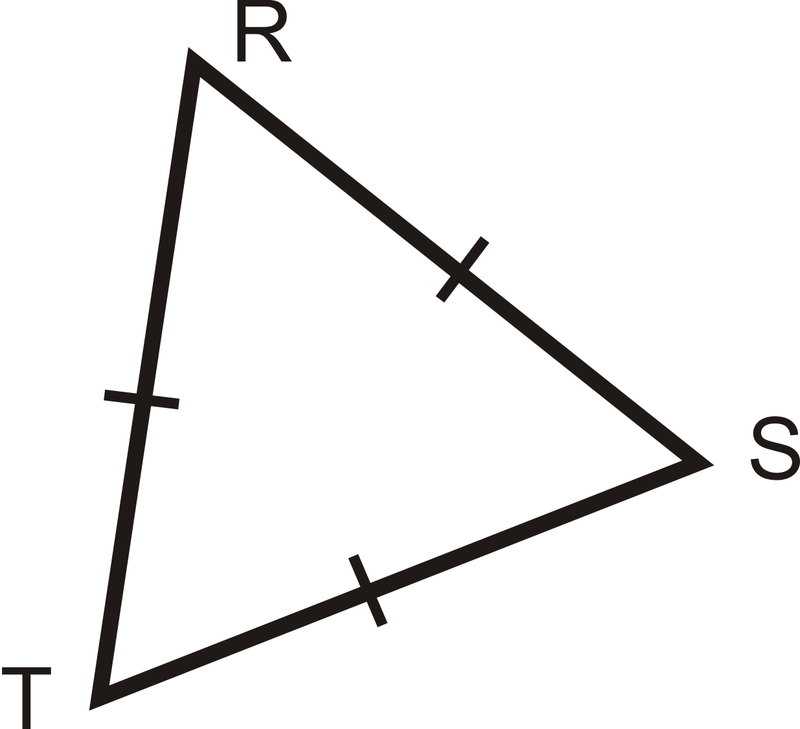
Рішення
| Заява | Причина |
|---|---|
| 1. | 1. Враховується |
| 2. | 2. Теорема про базові кути |
| 3. | 3. Теорема про базові кути |
| 4. | 4. Перехідний\(PoC\) |
| 5. \(\Delta RST\)рівнокутна | 5. |
| Заява | Причина |
|---|---|
| 1. \(RT\overline{AB}\cong ST\overline{AB}\cong RS\overline{AB}\) | 1. Враховується |
| 2. \(\angle R\cong \angle S\) | 2. Теорема про базові кути |
| 3. \(\angle T\cong \angle R\) | 3. Теорема про базові кути |
| 4. \(\angle T\cong \angle S\) | 4. Перехідний\(PoC\) |
| 5. \(\Delta RST\)рівнокутна | 5. Визначення рівнокутного. |
Приклад\(\PageIndex{2}\)
True або false: Всі рівносторонні трикутники є рівнобедреними трикутниками.
Рішення
Це твердження вірно. Визначення рівнобедреного трикутника - це трикутник з не менше двох конгруентних сторін. Оскільки всі рівносторонні трикутники мають три конгруентні сторони, вони підходять під визначення рівнобедреного трикутника.
Приклад\(\PageIndex{3}\)
Знайдіть значення\(x\).
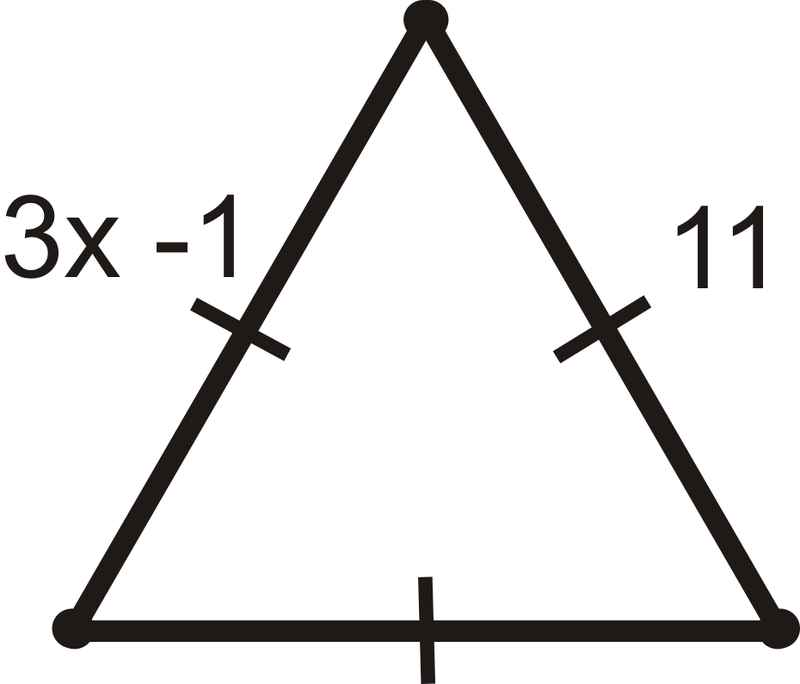
Рішення
Тому що це рівносторонній трикутник\(3x−1=11\). Вирішити для\(x\).
\(\bgin{align*} 3x−1&=11 \\3x&=12 \\ x&=4 \end{align*}\)
Приклад\(\PageIndex{4}\)
Знайдіть значення\(x\) і\(y\).
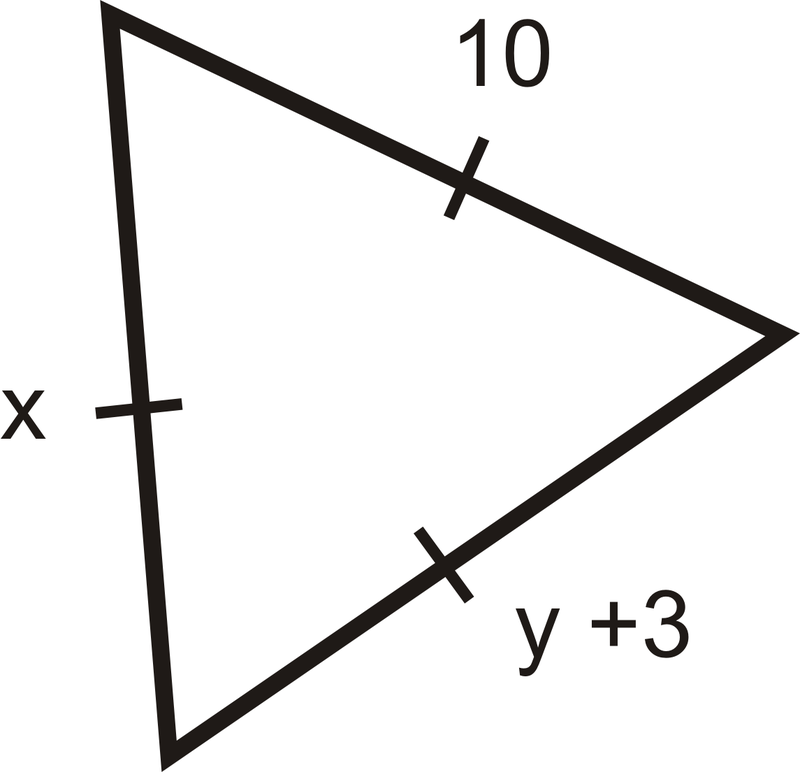
Рішення
Маркування показує, що це рівносторонній трикутник, оскільки всі сторони конгруентні. Це означає, що всі сторони повинні рівні\(10\). У нас є\(x=10\) і\(y+3=10\) що означає\(y=7\).
Приклад\(\PageIndex{5}\)
Дві сторони рівностороннього трикутника - це\(2x+5\) одиниці та\(x+13\) одиниці. Як довго кожна сторона цього трикутника?
Рішення
Дві задані сторони повинні бути рівними, оскільки це рівносторонній трикутник. Запишіть і вирішіть рівняння для\(x\).
\(\egin{align*}2x+5 &=x+13 \\ x&=8 \end{align*}\)
Щоб з'ясувати, як довго кожна сторона, підключіть 8 для\(x\) в будь-якому з оригінальних виразів. \(2(8)+5=21\). Кожна сторона - це\(21\) одиниці.
Рецензія
Наступні трикутники - це рівносторонні трикутники. Вирішити для невідомих змінних.
-

Малюнок\(\PageIndex{4}\) -
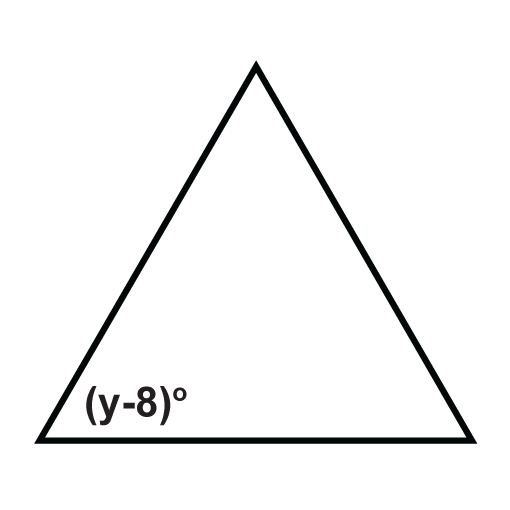
Малюнок\(\PageIndex{5}\) -
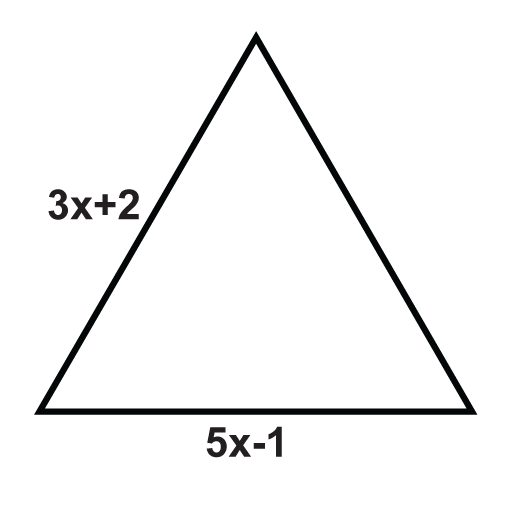
Малюнок\(\PageIndex{6}\) -

Малюнок\(\PageIndex{7}\) -
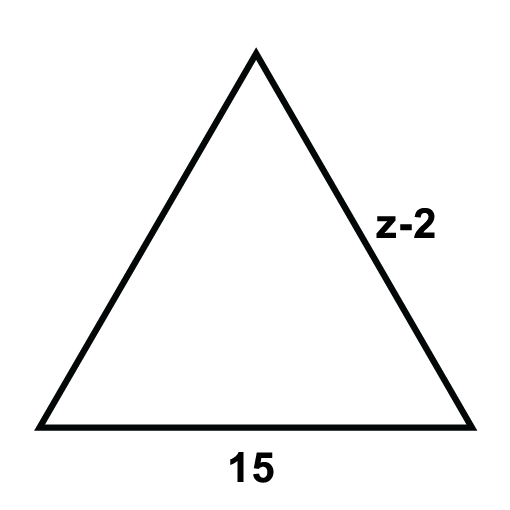
Малюнок\(\PageIndex{8}\) -

Малюнок\(\PageIndex{9}\) -
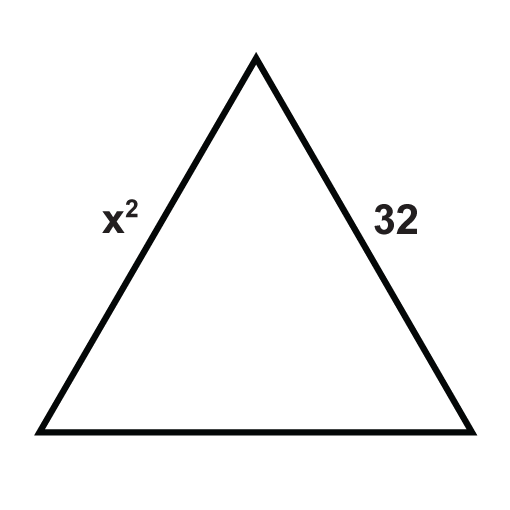
Малюнок\(\PageIndex{10}\) -
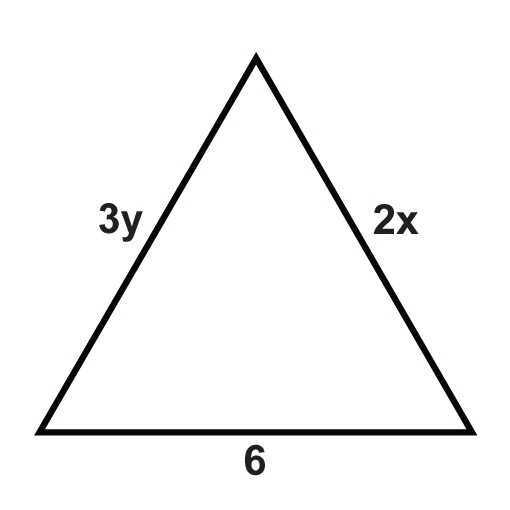
Малюнок\(\PageIndex{11}\) -
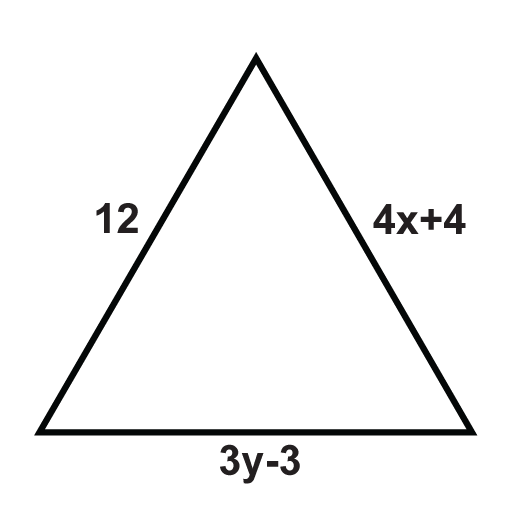
Малюнок\(\PageIndex{12}\) -
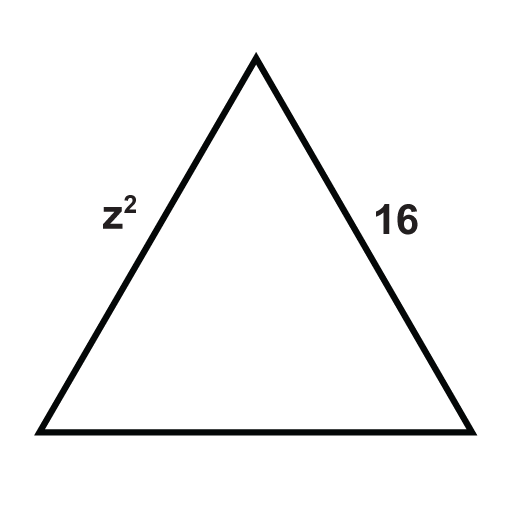
Малюнок\(\PageIndex{13}\) -
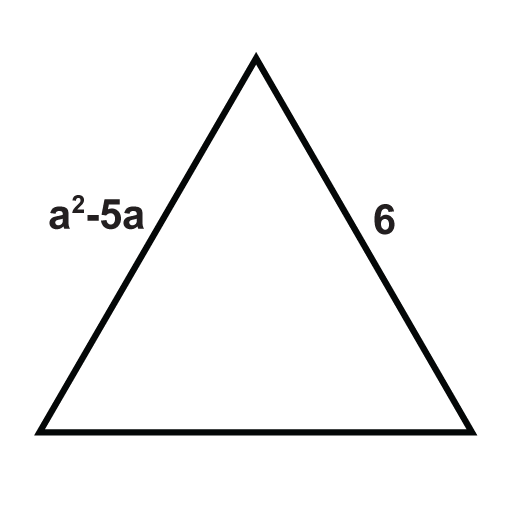
Малюнок\(\PageIndex{14}\) -
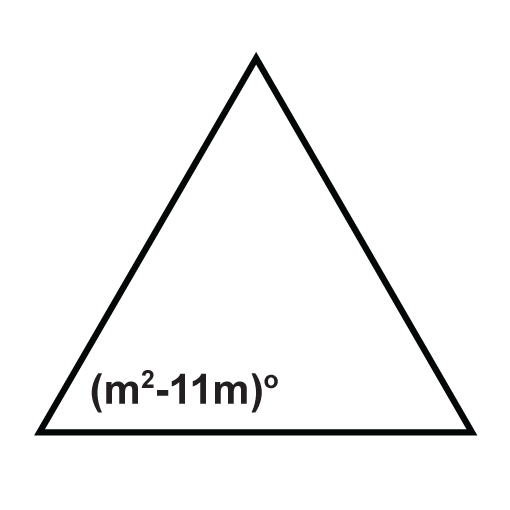
Малюнок\(\PageIndex{15}\) -

Малюнок\(\PageIndex{16}\) -
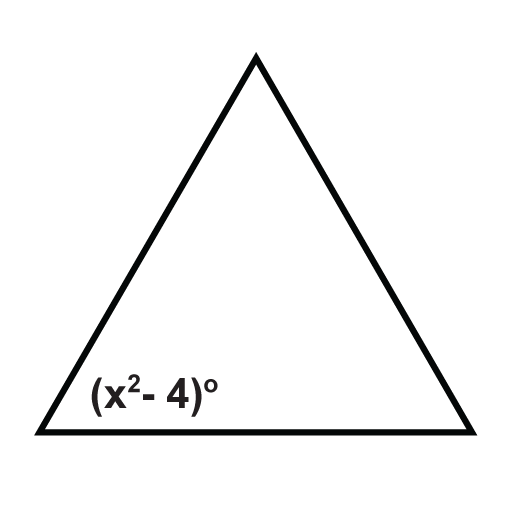
Малюнок\(\PageIndex{17}\) - Знайдіть міри\(x\) і\(y\).
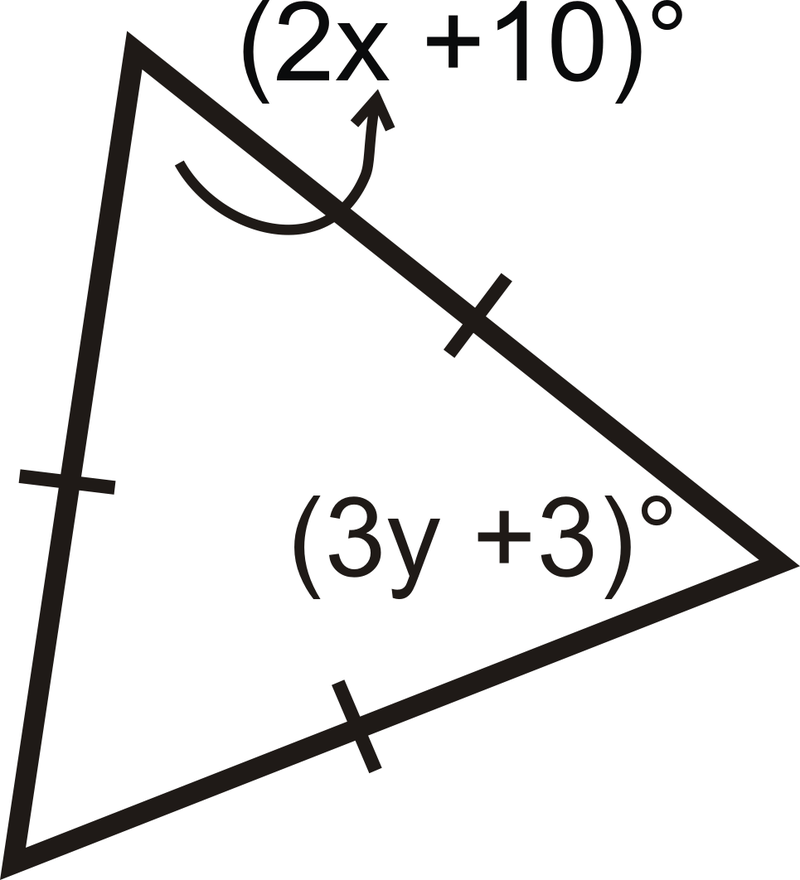
Огляд (Відповіді)
Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.11.
Додаткові ресурси
Інтерактивний елемент
Відео: Принципи рівносторонніх трикутників - Основні
Діяльність: Рівносторонні трикутники Дискусійні питання
Навчальні посібники: Питання для обговорення рівносторонніх трикутників
Практика: Рівносторонні трикутники
Реальний світ: Рівносторонні трикутники