4.4: Рівнобедрені трикутники

Last updated

Oct 27, 2022
Save as PDF
- 4.3: Класифікуйте трикутники за допомогою вимірювання сторони
- 4.5: Рівносторонні трикутники

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Властивості трикутників з двома рівними сторонами/кутами.

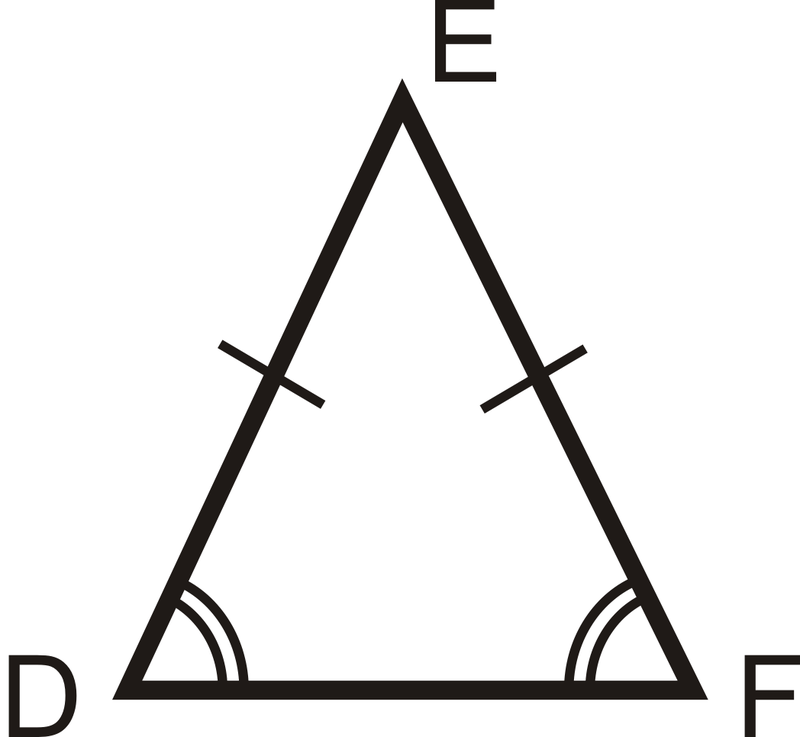
Рівнобедрений трикутник - це трикутник, який має принаймні дві конгруентні сторони. Конгруентні сторони рівнобедреного трикутника називаються ніжками. Інша сторона називається підставою. Кути між підставою і ніжками називаються базовими кутами. Кут, зроблений двома ніжками, називається кутом вершини. Однією з важливих властивостей рівнобедрених трикутників є те, що їх базові кути завжди конгруентні. Це називається теоремою базових кутів.

Для $\DeltaDEF, if \(\overline{DE}\cong \overline{EF}$ , тоді $\angle D\cong \angle F$ .

Ф-д_1С54Ф3ЕА2А10Ф06Е79ББ2058АА 20098632Е3 Е76423653Д63Д63С97Б9379+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Ще одна важлива властивість рівнобедрених трикутників полягає в тому, що кутова бісектриса кута вершини - це також перпендикулярна бісектриса підстави. Це називається теоремою про рівнобедрений трикутник. (Зауважте, що це стосується лише кута вершини. ) Вірні і зворотні теореми про базові кути та теореми про рівнобедрене трикутник.

Теорема про базові кути Converse: Якщо два кути в трикутнику конгруентні, то сторони, протилежні цим кутам, також конгруентні. Так для $\Delta DEF$ , якщо $\angle D\cong \angle F$ , то $\overline{DE}\cong \overline{EF}$ .

Теорема про рівнобедрений трикутник Converse: Перпендикулярна бісектриса підстави рівнобедреного трикутника також є кутовою бісектрисою кута вершини. Так для рівнобедрених $\DeltaDEF$ , якщо $\overline{EG}\perp \overline{DF}$ і $\overline{DG}\cong \overline{GF}$ , то $\angle DEG\cong \angle FEG$ .

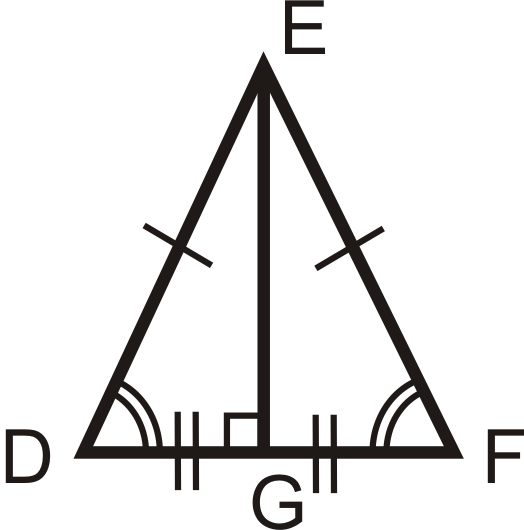
F-D_56АЕ15Ф55АЕ 39176 ДД1А9234КБСБ 685 А17ДА705СА78Е1ББ ББ 75БК40Б6+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Що робити, якщо вам подарували рівнобедрений трикутник і сказали, що його базові кути вимірюють $x^{\circ}$ і $y^{\circ}$ ? Що ви могли б зробити висновок про $x$ і $y$ ?

Приклад $\PageIndex{1}$

Знайдіть значення $x$ і міру кожного кута.

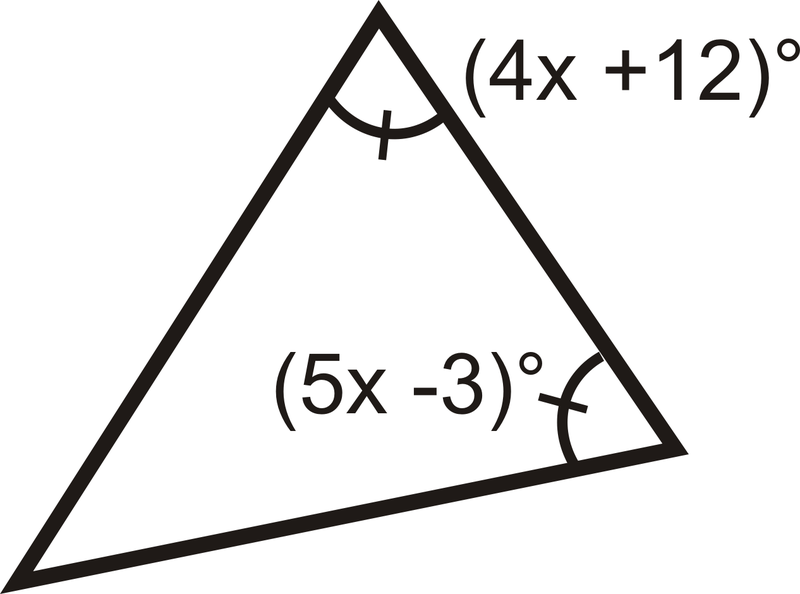
Ф-д_731А3Ф2Е0А2759С55Е6 ЕДДДД4Д87Е2Ф34ФА486 AEEC81170343 ББ52007+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Рішення

Два кута рівні, тому встановіть їх рівними один одному і вирішуйте для $x$ .

$\begin{align*} (4x+12)^{\circ}&=(5x−3)^{\circ} \\ 15&=x\end{align*}$

Заставте x = 15; базові кути є $[4(15)+12]^{\circ}$ , або 72^ {\ circ}\). Кут вершини дорівнює $180^{\circ}−72^{\circ}−72^{\circ}=36^{\circ}$ .

Приклад $\PageIndex{2}$

True або false: Базові кути рівнобедреного трикутника можуть бути прямими кутами.

Рішення

Це твердження є помилковим. Оскільки базові кути рівнобедреного трикутника є конгруентними, якщо один базовий кут є прямим кутом, то обидва базові кути повинні бути прямими кутами. Неможливо мати трикутник з двома прямими ( $90^{\circ}$ ) кутами. Теорема про суму трикутника стверджує, що сума трьох кутів у трикутнику дорівнює $180^{\circ}$ . Якщо два кути в трикутнику є прямими кутами, то третій кут повинен бути $0^{\circ}$ і форма вже не трикутник.

Приклад $\PageIndex{3}$

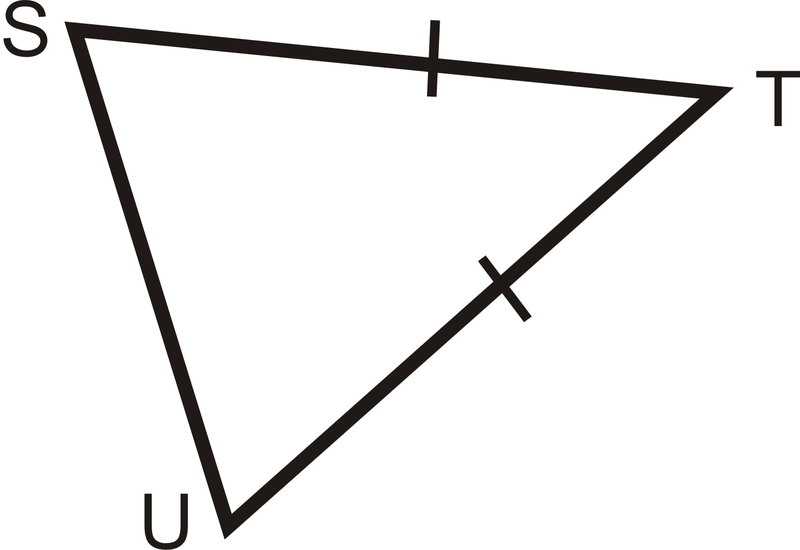
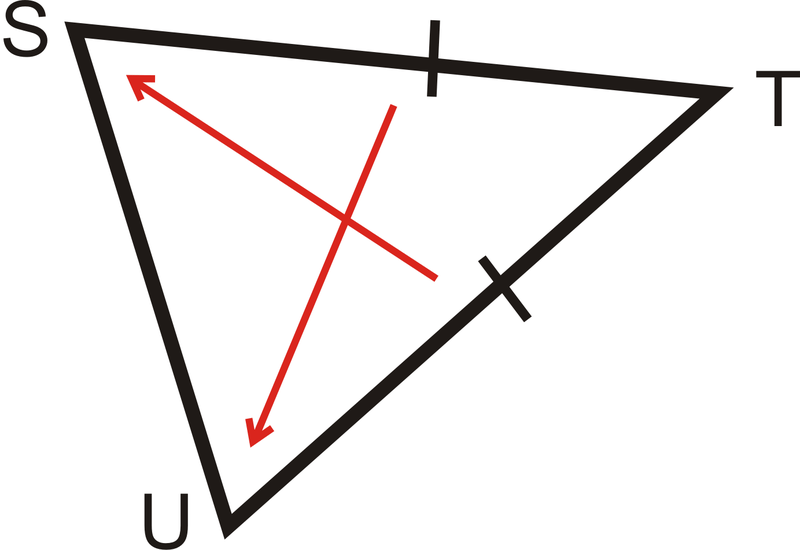
Які два кути є конгруентними?

F-D_DC 6CD-BE7E 50c766d7869A48 БД2779096Ф9Ф9Ф55А7Д8 ББ8371Б8C696165+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{5}$

Рішення

Це рівнобедрений трикутник. Конгруентні кути знаходяться навпроти конгруентних сторін. Зі стрілок бачимо, що $\angle S\cong \angle U$ .

Ф-Д_1Ф0С4Е5Д917БА80ББ15Б20Ф ББ 33А7С20С4Ф96Ф9153079БК202С81CF+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{6}$

Приклад $\PageIndex{4}$

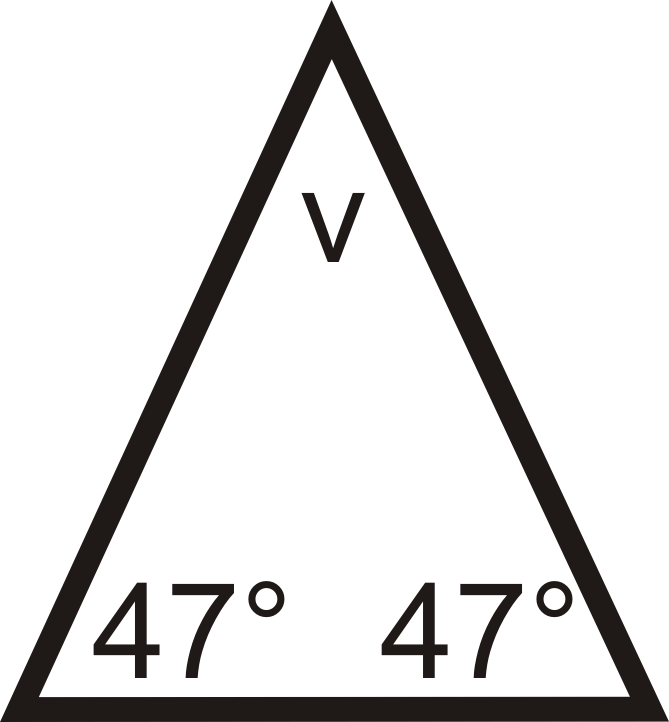
Якщо рівнобедрений трикутник має базові кути з мірами $47^{\circ}$ , яка міра кута вершини?

F-д_7863 А282Ф3Б281А311А8ФБ298Ф5СБ1АД 1Б56274FF2Б564AFCFB30+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{7}$

Рішення

Намалюйте малюнок і встановіть рівняння для вирішення кута вершини, $v$ . Пам'ятайте, що три кути в трикутнику завжди складаються до $180^{\circ}$ .

$\begin{align*} 47^{\circ}+47^{\circ}+v &=180^{\circ} \\ v &=180^{\circ}−47^{\circ}−47^{\circ} \\ v =86^{\circ} \end{align}$

Приклад $\PageIndex{5}$

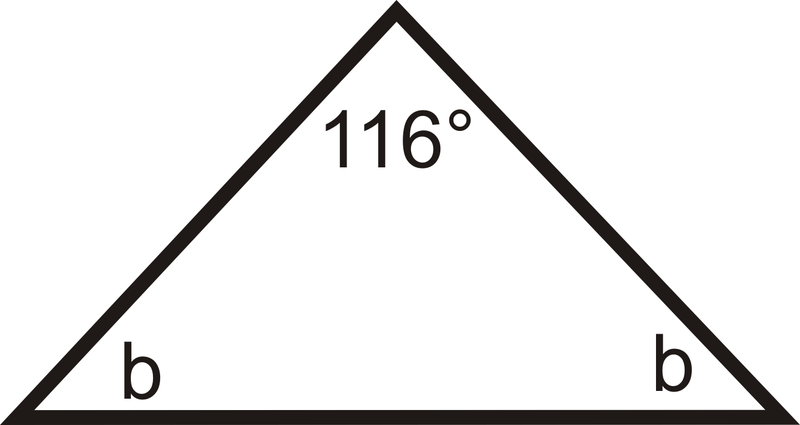
Якщо рівнобедрений трикутник має кут вершини з мірою $116^{\circ}$ , яка міра кожного базового кута?

Ф-д_90б69ф3д д 3Е339566Ф6Ф6Ф6Ф242Д 7Ф168736Б395Ф473А3А33+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{8}$

Рішення

Намалюйте малюнок і налаштуйте і рівняння для вирішення базових кутів, $b$ .

$\begin{align*} 116^{\circ}+b+b&=180^{\circ} \\ 2b&=64^{\circ} \\ b &=32^{\circ}\end{align*}$

Рецензія

Знайти заходи $x$ та/або $y$ .

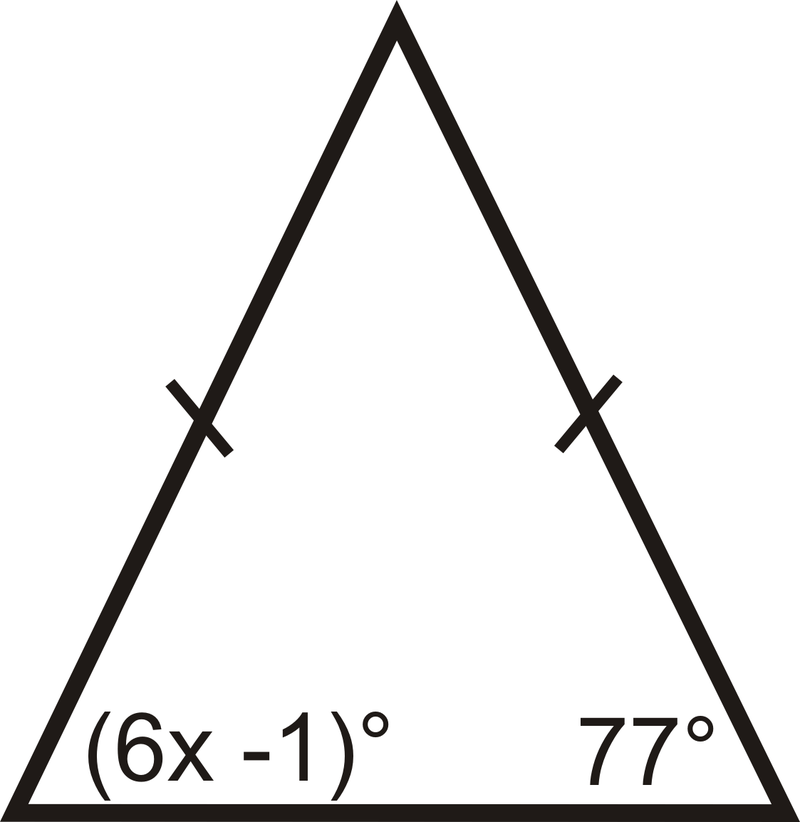
Малюнок $\PageIndex{9}$
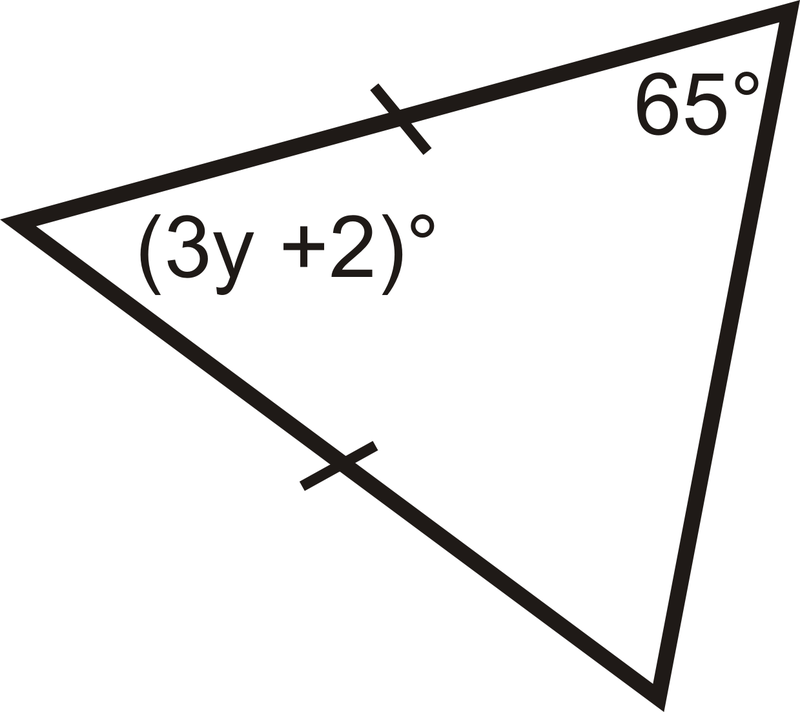
Малюнок $\PageIndex{10}$
Малюнок $\PageIndex{11}$
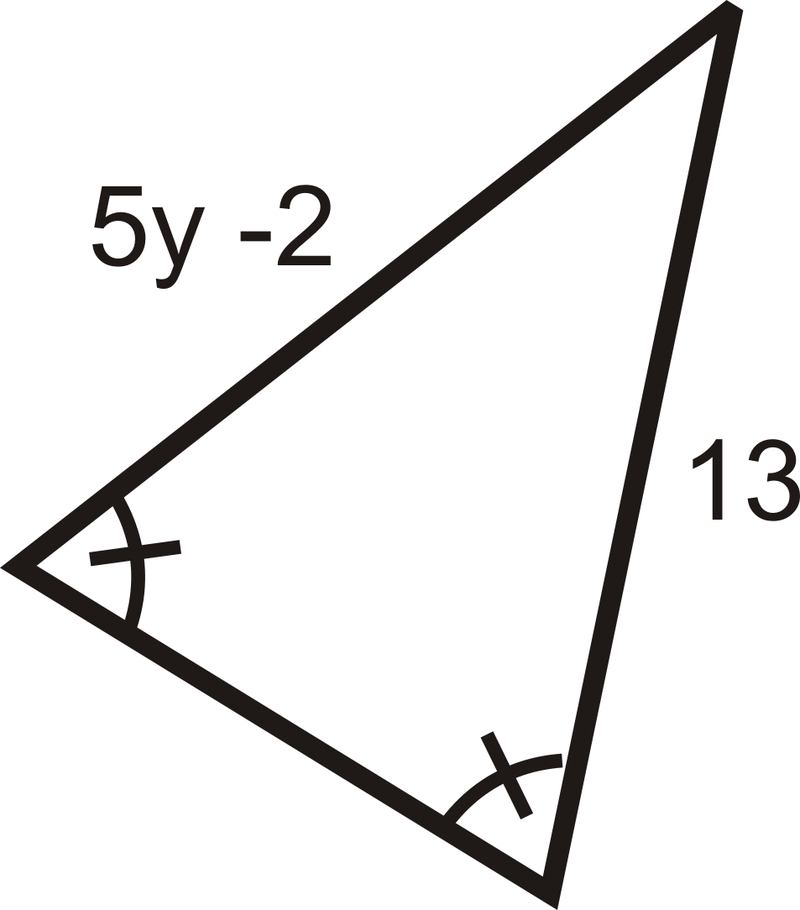
Малюнок $\PageIndex{12}$
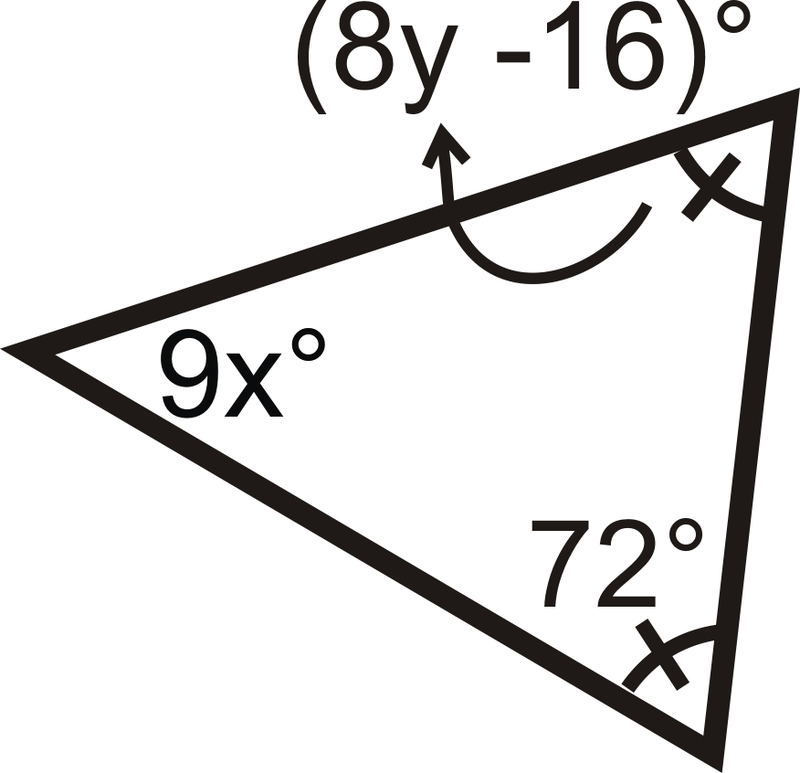
Малюнок $\PageIndex{13}$

Визначте, чи є наступні твердження істинними чи хибними.

Базові кути рівнобедреного трикутника конгруентні.
Базові кути рівнобедреного трикутника є взаємодоповнюючими.
Базові кути рівнобедреного трикутника можуть дорівнювати куту вершини.
Базові кути рівнобедреного трикутника гострі.

Заповніть докази нижче.

Дано: Рівнобедрений $\DeltaCIS$ , з базовими кутами $\angle C$ і $\angle S$ . \ overline {IO}\) - бісектриса кута $\angle CIS$ Prove: $\overline{IO}$ перпендикулярна бісектриса $\overline{CS}$

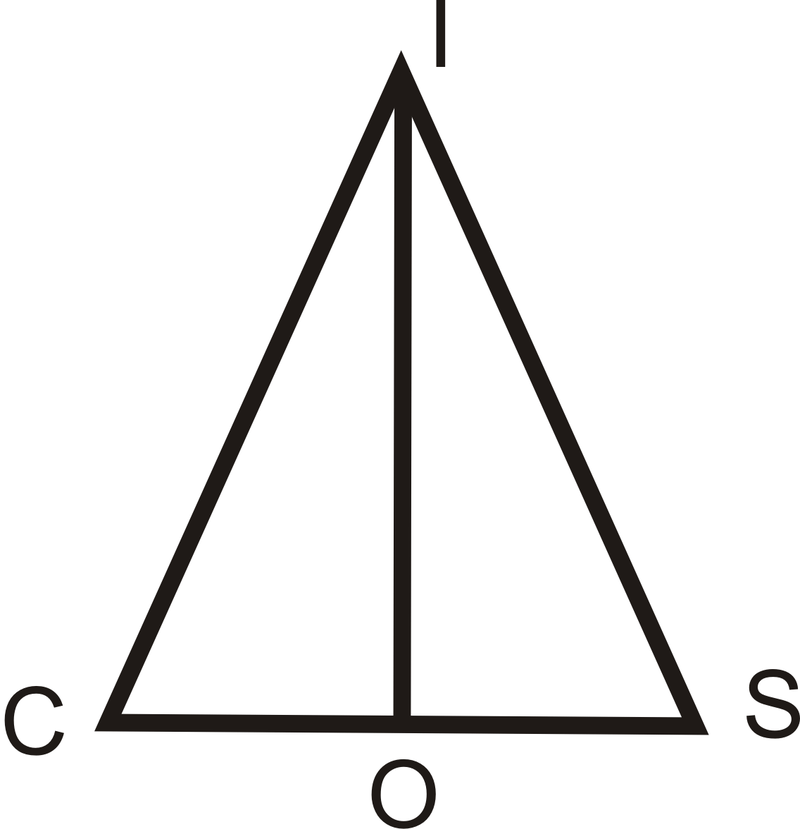
F-д_86710951 ЗК д 60ФК1Е610А6006А9Б85087731Б60338Б197Б133E18029+зображення_крихіткий+зображення_крихіткий_png — Малюнок $\PageIndex{14}$

*Заява*	*Причина*
1.	1. Враховується
2.	2. Теорема про базові кути
3. $\angle CIO\cong \angle SIO$	3.
4.	4. Рефлексивний $PoC$
5. $\DeltaCIO\cong \DeltaSIO$	5.
6. $\overline{CO}\cong \overline{OS}$	6.
7.	7. $CPCTC$
8. $\angle IOC$ і $\angle IOS$ є додатковими	8.
9.	9. Теорема про конгруентні добавки
10. $\overline{IO}$ перпендикулярна бісектриса $\overline{CS}$	10.

Дано: $\DeltaICS$ Рівнобедрений з $\angle C$ і $\angle S$ . $\overline{IO}$ перпендикулярна бісектриса $\overline{CS}$ $\overline{IO}$ Дове: це бісектриса кута $\angle CIS$

*Заява*	*Причина*
1.	1.
2. $\angle C\cong \angle S$	2.
3. $CO\overline{AB}\cong OS\overline{AB}$	3.
4. $m\angle IOC=m\angle IOS=90^{\circ}$	4.
5.	5.
6.	6. $CPCTC$
7. $\overline{IO}$ є кутовою бісектрисою $\angle CIS$	7.

На площині x−y побудуйте координати та визначте, чи задані три точки складають сходовий або рівнобедрений трикутник.

$(-2, 1), (1, -2), (-5, -2)$
$(-2, 5), (2, 4), (0, -1)$
$(6, 9), (12, 3), (3, -6)$
$(-10, -5), (-8, 5), (2, 3)$
$(-1, 2), (7, 2), (3, 9)$

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.10.

Ресурси

Лексика

Термін	Визначення
База	Сторона трикутника, паралельна нижньому краю паперу або екрану, прийнято називати основою. Підставою рівнобедреного трикутника є неконгруентна сторона в трикутнику.
Базові кути	Базові кути рівнобедреного трикутника - це кути, утворені підставою і однією ніжкою трикутника.
Теорема про базові кути	Теорема базових кутів обертається, якщо два кути в трикутнику конгруентні, то сторони, протилежні цим кутам, також є конгруентними.
Теорема про рівнобедрене трикутник	Теорема про рівнобедрений трикутник стверджує, що перпендикулярна бісектриса підстави рівнобедреного трикутника також є кутовою бісектрисою кута вершини.
Теорема про суму трикутника	Теорема про суму трикутника стверджує, що три внутрішні кути будь-якого трикутника складають до 180 градусів.
Вертикальні кути	Вертикальні кути - це пара протилежних кутів, створених пересічними лініями.

Додаткові ресурси

Інтерактивний елемент

Відео: Принципи рівнобедрених трикутників - Основні

Діяльність: Рівнобедрені трикутники Обговорення Питання

Навчальні посібники: Посібник з вивчення відносин з

Практика: Рівнобедрені трикутники

Реальний світ: Трикутники в небі