13: Ефекти пов'язаного виділення
- Page ID
- 7796
Генетичний дрейф - не єдине джерело випадковості в динаміці алелей. Алелі також відчувають випадкові коливання частоти через те, що вони присутні на наборі випадкових генетичних фонів з різною фітнесом. Наприклад, коли корисний алель виникає через одну мутацію, він виникає на певному генетичному фоні, тобто певному гаплотипі (рис.\ ref {Fig:HIV_Sweep} A). Уявіть собі цю мутацію, що виникає в регіоні без рекомбінації, або в організмі, де генетичний обмін зустрічається рідко. Якщо наш корисний алель встановиться в популяції, тобто уникає втрати генетичним дрейфом у тих перших кількох поколіннях, він почне швидко збільшуватися. Як він збільшується в частоті, так і алелі, які трапилися бути присутніми на гаплотипі, на якому виникла мутація (якщо ці інші алелі нейтральні або принаймні не надто шкідливі). Ці інші алелі добираються до «автостопом» разом. Алелі, які не знаходяться на цьому конкретному тлі, змітаються з популяції, тому чистий ефект цієї селективної розгортки полягає у видаленні генетичного різноманіття з популяції. Різноманітність врешті-решт відновиться, оскільки виникають нові мутації, а деякі повільно дрейфують по частоті. Але в короткостроковій перспективі селективні розгортки видаляють генетичні варіації з популяцій.
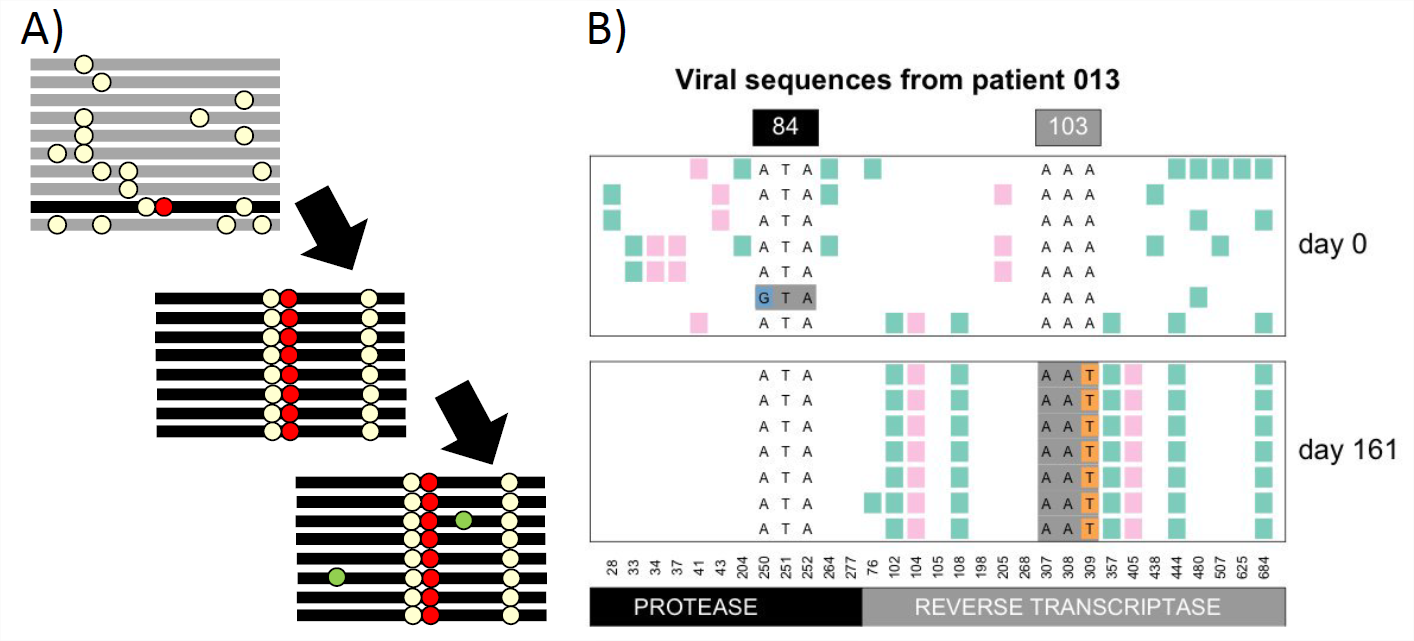
illiams548198 візуалізували селективні розгортки при ВІЛ. На малюнку\ ref {Fig:HIV_Sweep} B) ми бачимо набір гаплотипів ВІЛ, відібраних у пацієнта до і після селективного розгортання лікарської стійкої мутації. Пацієнт приймає інгібітор ретротранспози (Ефавіренц), але, на жаль, протягом 161 дня виникла і поширилася стійка до ліків мутація, яка змінює білок ретротранспозази ВІЛ. Зверніть увагу, як конкретний гаплотип тепер зафіксований у зразку, і залишається мало генетичного різноманіття, завдяки ефекту автостопа сильної селективної розгортки цього алеля.
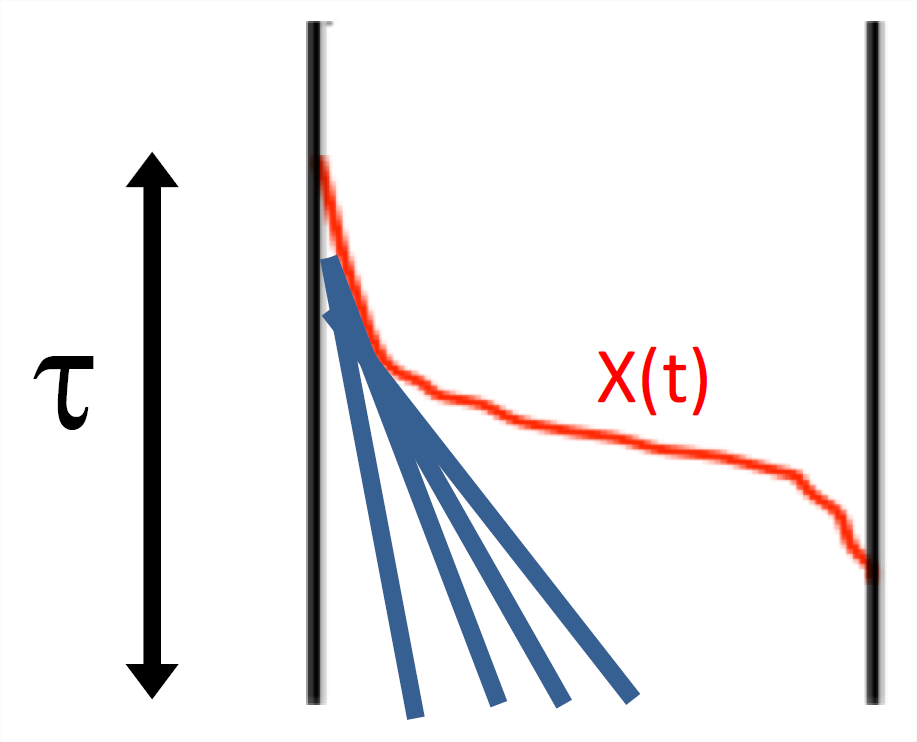
Щоб краще зрозуміти автостопом, спочатку давайте уявимо, що вивчаємо варіацію в локусі, повністю пов'язаному з нашим вибраним локусом, відразу після того, як наша розгортка досягла фіксації. Нейтральні алелі, відібрані в цьому місці, повинні простежити свої родові лінії назад до нейтрального алеля, на тлі якого спочатку виник обраний алель (рис.\ ref {fig:no_recom_coal}). Це пов'язано з тим, що той фоновий нейтральний алель, який існував\(\tau\) покоління тому, є родоначальником всієї популяції в цьому повністю пов'язаному локусі. Наші особи, які несуть корисний алель, з точки зору цих алелів відчувають швидко зростаючу популяцію. Тому пара нейтральних алелів, відібраних у нашому зв'язаному нейтральному локусі, буде змушена об'єднатися\(\approx \tau\) поколіннями тому. Нещодавно отриманий алель з коефіцієнтом адитивного відбору\(s\) займе час\(\tau = 4\log(2N)/s\) поколінь, щоб досягти фіксації всередині нашої популяції (див. Рівняння\ ref {eq:diploid_fix_time}). Це дуже короткочасна шкала в порівнянні з середнім нейтральним часом коалесценції\(2N\) поколінь для пари алелей. Таким чином, ми очікуємо незначних змін, оскільки на цих дуже коротких гілках виникне мало мутацій, а ті, що зробили, швидше за все, будуть синглетонами у нашому зразку.
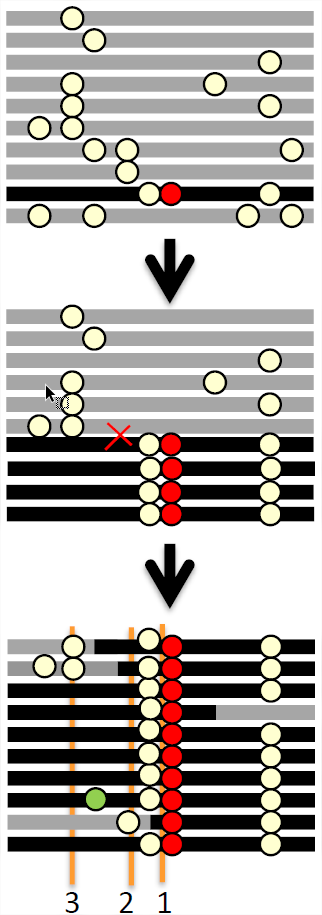
Тепер давайте подумаємо про розгортку в рекомбінуючому регіоні. Знову вибрана мутація виникає на конкретному гаплотипі, і він і його гаплотип починає збільшуватися в частоті в популяції (рис.\ ref {fig:sweep_haps}). Однак зараз рекомбінаційні події можуть відбуватися між гаплотипами, що несуть і не несуть обраний алель, у осіб, які є гетерозиготою для обраного алеля. Ці рекомбінаційні події дозволяють алелям, яких не було на оригінальному обраному гаплотипі, уникнути викидання з популяції, а також дещо відокремити обраний алель від автостопів, заважаючи багатьом з них автостопом весь шлях до фіксації. Далеко від обраного сайту швидкість рекомбінації досить висока, щоб алелі, які були присутні на початковому тлі, ледве потрапляють в автостоп разом, оскільки рекомбінація дуже швидко розриває їх асоціацію з вибраним алелем.

Як виглядають коалесцентні генеалогії на локусах на різних відстанях від обраної ділянки? Ну, близько до вибраного сайту всі наші алелі в даний час простежуються назад до найновішого загального родового алелю присутній на цьому вибраному гаплотипі, і тому всі вони змушені зливатися навколо\(\tau\) поколінь тому (місце 1, див. Рис.\ ref {fig:sweep_haps_coal}). Трохи далі від вибраного сайту (локус 2), у нас є лінії, які не простежують своє походження назад до оригінального вибраного гаплотипу, але замість цього походять від рекомбінантних гаплотипів, які рекомбінуються на розгортку (гаплотип другий знизу на малюнку\ ref {fig:sweep_haps_coal}). Ці лінії можуть нейтрально зливатися з іншими родовими лініями протягом набагато глибших часових масштабів, а мутації на цих глибоких лініях відповідають постійній різноманітності, присутній у нашому населенні до розгортки. Коли ми рухаємося ще далі від обраного сайту (локус 3), ми стикаємося з дедалі більшою кількістю ліній, що походять від рекомбінантних гаплотипів, які об'єднуються нейтрально набагато глибше в часі\(\tau\), ніж, дозволяючи різноманітності відновлюватися до фонових рівнів, коли ми віддаляємося від обраного сайту (див. Рисунок\ ref {fig:автостоп_скорочення}).

Щоб змоделювати очікувану картину різноманітності, що оточує вибрану ділянку, ми можемо подумати про пару алелів, відібраних на нейтральному місці на\(c\) відстані рекомбінації від нашого обраного сайту. Наша пара алелів буде змушена зливатися\(\approx \tau\) поколіннями, якщо жоден з них не походить від рекомбінантних гаплотипів (Ліва сторона рисунка\ ref {fig:recom_coal}).

Імовірність того, що наші алелі в нашому нейтральному локусі походять від предкового гаплотипу, на якому відбувається обраний алель, тобто що алель не сходить з рекомбінантного гаплотипу, становить
\[p_{NR} = e^{-c \tau/2 }. \label{eqn:prob_no_recom_sweep}\]
Яка інтуїція для цього werll є\(\tau\) покоління, в яких може відбуватися рекомбінація, тому приблизно ймовірність того, що абсолютно ніякої рекомбінації не відбувається\((1-c)^{\tau} =\approx e^{-c\tau}\). Звідки береться коефіцієнт\(\frac{1}{2}\) in\ ref {eqn:prob_no_recom_sweep}? Ну для того, щоб рекомбінувати алель з обраного фону, рекомбінація повинна відбуватися в гетерозиготі для обраного алеля, при адитивній моделі нейтральний алель, пов'язаний з повністю розмашистим алелем, витрачає в середньому\(\frac{1}{2}\) свій час в гетерозйотах, тому знижуючи наш ефективний швидкість рекомбінації в два рази (докладніше див. Додаток 2 в кінці глави).
Імовірність того, що жодна з наших ліній не походить від рекомбінантного гаплотипу і, отже, змушені зливатися, є\(p_{NR}^2\) (якщо припустити, що вони зливаються в момент, близький до\(\tau\) так, що вони рекомбінуються незалежно один від одного протягом разів\(< \tau\)). Якщо одна чи інша з наших родовищ походить від рекомбінантного гаплотипу, їм знадобиться в середньому\(\approx 2N\) поколіннях, щоб знайти спільного предка, оскільки ми повертаємось до наших нейтральних коалесцентних ймовірностей (Права сторона рисунка\ ref {fig:local_sweep_haps}). Таким чином, очікуваний час, поки наша пара родовищ не знайде спільного предка
\[\mathbb{E}(T_2) = \tau \times p_{NR}^2 +(1-p_{NR}^2) (\tau +2N) \approx \left(1-p_{NR}^2 \right) 2N\]
де це останнє наближення передбачає, що\(\tau \ll 2N\). Отже, очікувана попарна різноманітність для нейтральних алелів на відстані рекомбінації\(r\) від вибраної розгортки (\(\pi_c\)) становить
\[\mathbb{E}(\pi_c) = 2\mu \mathbb{E}(T_2) \approx \pi_0 \left(1-e^{-c\tau} \right) \label{eqn:pi_HH}\]
Тож різноманітність збільшується, коли ми віддаляємось від обраної ділянки, повільно та експоненціально плавучи до його нейтрального очікування\(\pi_0\).

Збудник малярії (Plasmodium falciparum) розвинув стійкість до препаратів проти малярії, часто шляхом змін гена dhfr. Рисунок\ ref {fig:hitchhiking_malaria} показує рівні генетичного різноманіття (гетерозиготності) при наборі маркерів, що виходять з гена dhfr в наборі стійких до ліків послідовностей малярії, зібраних в Таїланді. Ми бачимо характерне падіння різноманітності навколо гена, з нульовою різноманітністю в ряді локусів, дуже близьких до гена, що свідчить про сильну селективну розгортку. Підібравши нашу просту модель розгортки до цих даних, ми оцінюємо, що\(\tau \approx 40\) покоління, що відповідають фіксації алелів лікарської стійкості за дуже короткий проміжок часу.

Щоб отримати відчуття фізичного масштабу, над яким зменшується різноманітність, розглянемо область, де рекомбінація відбувається зі швидкістю\(c_{BP}\) на базову пару на покоління, і локус\(\ell\) бази пари подалі від обраного сайту, наприклад, що\(c=c_{BP } \ell\) (де \(c_{BP} \ell \ll 1\)тому нам не потрібно турбуватися про більш ніж одну подію рекомбінації, що відбувається на покоління). Типові показники рекомбінації знаходяться на порядку\(c_{BP} = 10^{-8}\). На малюнку\ ref {fig:hitchhiking_reduction} показано зменшення різноманітності, задане Equation\ ref {eqn:pi_hh}, для двох різних коефіцієнтів відбору.
Для того, щоб наш очікуваний рівень різноманітності відновився до\(50\%\) свого нейтрального очікування\(\mathbb{E}(\pi_c)/\theta=0.5\), потрібна фізична відстань,\(\ell^{*}\) така\(\log(0.5) = -x_{BP} \ell ^*\tau\), що, і шляхом перестановки,
\[\ell^* = \frac{-\log(0.5)}{c_{BP} \tau }.\]
Як обернено\(\tau\) залежить від вибору\(s\) (Equation\ ref {eq:diploid_fix_time}), ширина нашого корита зменшеної різноманітності залежить від\(s/c_{BP}\). За інших рівних умов ми очікуємо, що більш сильні розгортки або розгортки в регіонах з низькою рекомбінацією матимуть більший ефект автостопа. Наприклад, у геномній області зі швидкістю рекомбінації\(c_{BP}=10^{-8}\) bp\(^{-1}\) коефіцієнт відбору зменшить різноманітність понад 10\(s=0.1\%\) кб, тоді як розгортка вплине на\(\sim\) 100kb.\(s=1\%\)
виявлено генетичну основу меланізму у перцевої молі (Biston betularia). Цей алель охопився до фіксації в північних районах Великобританії; класичний випадок адаптації до промислового забруднення (прославився роботою, см і). Генетичною основою меланзму є транспозіруемий елемент (TE), вставлений у ген пігментації. встановлено, що різноманітність пригнічується в широкій області навколо TE. Зокрема, на тлі TE потрібно приблизно 200 кб в будь-якому напрямку, щоб рівень різноманітності відновився до 50% загальногеномних рівнів.
Випадкові факти: У всіх метеликів і метеликів рекомбінуються тільки самці; хромосоми передаються без рекомбінації у самок. Швидкість рекомбінації у чоловіків становить 2,9 см/Мб. Поперчені молі мають ефективний розмір популяції приблизно в сто тисяч особин. Kettlewell вживав в їжу метеликів, коли збирали їх у полі (особисте спілкування, ст. Шапіро).
- Коротко поясніть, як ця модель пропонує додаткові докази того, що мелановий алель був сприятливий при відборі.
- Використовуючи цю інформацію, і припускаючи, що вплив алеля на фітнес є адитивними, яка ваша оцінка віку алеля?
- Яка ваша оцінка коефіцієнта відбору, що сприяє цьому мелановому алелю?

Інші сигнали вибіркових розгорток
Первинним сигналом нещодавно завершеної селективної розгортки є характерне зменшення різноманітності навколо обраної ділянки. Однак розгортки залишають інші сигнали, і вони також часто використовуються для ідентифікації локусів, які проходять відбір. Наприклад, нейтральні алелі далі від обраної ділянки можуть відступити лише частину шляху до фіксації, якщо під час розгортки відбувається рекомбінація, що може призвести до надлишку високочастотних отриманих алелей на проміжних відстанях від обраної ділянки, що триває короткий час після підмітати. Крім того, оскільки нейтральні рівні різноманітності повільно відновлюються через приплив нових мутацій після розгортки, спостерігається сильний перекіс до алелів, отриманих низькою частотою, - закономірність, яка зберігається протягом багатьох поколінь. Надлишок рідкісних алелей, порівняно з нейтральною моделлю, може бути зафіксований статистикою, такою як D Tajima (з якою ми зіткнулися ще в нашому обговоренні частоти нейтрального сайту eqn\ ref {eqn_tajimas_d}). Таким чином, одним із способів пошуку локусів, які зазнали селективних розгорток, є обчислення D Tajima з даних у вікні вздовж генома та шукати сильні відхилення від нульового розподілу.
[Мал.: local_sweep_haps]
Ми також можемо використовувати порівняння між кількома популяціями для пошуку доказів того, що відбувається в одній з популяцій, наприклад, для виявлення алелів, що беруть участь у локальній адаптації (див.\ ref {fig:local_sweep_haps}). Вибіркова розгортка зменшить різноманітність всередині населення (\(H_S\)), що оточує вибрану ділянку, не впливаючи на різноманітність між різними популяціями. Таким чином, місцеві розгортки створюють піки\(F_{\mathrm{ST}}\) між слабо диференційованими популяціями.
вивчено загальногеномні закономірності\(F_{\mathrm{ST}}\) між морськими та прісноводними популяціями трихребтової колючки (Gasterosteus aculeatus), побудовані на малюнку\ ref {fig:local_sweep_stickleback}. Між різними морськими популяціями вони не виявили сильних вершин\(F_{\mathrm{ST}}\); однак між морськими та прісноводними порівняннями вони виявили ряд високих\(F_{\mathrm{ST}}\) піків, які були відтворені протягом ряду прісноводних морських порівнянь. Вони визначили ряд нових регіонів, відповідальних за адаптацію колючок до прісноводних середовищ, а також ряд локусів, раніше виявлених у схрещуваннях між морськими та прісноводними популяціями. Наприклад, перший пік Linkage Group IV включає ектодисплазин А (Еда), ген, який бере участь у адаптивній втраті броньового покриття в прісноводних середовищах.
[Мал.: local_sweep_паличка назад]
М'які розгортки від декількох мутацій і стоячих варіацій.
У нашій моделі розгортки вище ми припустили, що вибір сприяє корисному алелю з моменту, коли він увійшов до популяції як мутація однієї копії (ліва панель, рис.\ ref {fig:soft_sweep_haps}). Однак при включенні нового тиску селекції кілька мутацій в одному гені можуть почати розгортатися, так що жоден з цих алелів не підмітає до фіксації (середня панель, рис.\ ref {fig:soft_sweep_haps}). Ці розгортки, що включають кілька мутацій, значно пом'якшують вплив селекції на геномне різноманіття, і тому називаються «м'якими розгортками».
[Мал.: софт_sweep_haps]
Ще один спосіб, яким вплив розгортки може бути пом'якшений, - це якщо наш алель деякий час відокремлювався в популяції, перш ніж він став корисним. Цей додатковий час означає, що наш алель може рекомбінуватися на різні гаплотипи фонів, так що при перемиканні тиску вибору вибраний алель змітається по частоті на декількох різних гаплотипах (права панель, рис.\ ref {fig:soft_sweep_haps}). Виявлення та диференціація цих різних типів розгорток є активною сферою емпіричних досліджень та теорії в популяційній геноміці (див. Огляд розробок у цій галузі).
Загальногеномні ефекти пов'язаної селекції.
Якою мірою є закономірності варіацій уздовж генома та серед видів, сформованих пов'язаним відбором, наприклад, селективні розгортки? Ми можемо сподіватися на виявлення окремих випадків сильних селективних промахів уздовж генома, але як вони сприяють більш широким моделям варіації?
Два спостереження спантеличили популяційних генетиків з моменту створення молекулярної популяційної генетики. Перший - відносно високий рівень генетичної варіації, що спостерігається у більшості обов'язково статевих видів. Нейтральна теорія молекулярної еволюції була розроблена частково, щоб пояснити ці високі рівні різноманітності. Як ми бачили в розділі\ ref {Chapter:Drift}, за простою нейтральною моделлю, з постійною чисельністю популяції, слід очікувати, що кількість нейтрального генетичного різноманіття буде масштабуватися з добутком чисельності популяції та швидкості мутації. Друге спостереження, однак, є відносно вузьким діапазоном поліморфізму серед видів із значно різними розмірами перепису (див. Рис.\ ref {рис:Leffer} та недавній огляд). Як підкреслив у своєму обговоренні парадоксу варіації, це спостереження, здавалося б, суперечить прогнозуванню нейтральної теорії про те, що генетичне різноманіття повинно масштабуватися з чисельністю населення перепису населення. Існує ряд пояснень розбіжності між рівнями генетичного різноманіття та чисельністю населення перепису населення. Перший полягає в тому, що ефективний розмір населення (\(N_e\)) часто набагато нижчий за розмір перепису, через високу дисперсію в репродуктивному успіху та часті вузькі місця (як обговорюється в розділі\ ref {Chapter:Drift}). Друге основне пояснення, висунуте, полягає в тому, що нейтральні рівні різноманітності також систематично знижуються наслідками пов'язаного відбору. У великих популяціях селективні розгортки та інші форми пов'язаного відбору можуть домінувати над генетичним дрейфом як джерелом стохастичності в частотах алелів, потенційно встановлюючи верхню межу рівнів різноманітності.
[Рис: GW_автостопом похід_скорочення]
Однією з сильних доказів дії пов'язаної селекції при зниженні рівнів поліморфізму є позитивна кореляція між передбачувано нейтральною різноманітністю та рекомбінацією, що спостерігається у ряді видів, оскільки, за інших рівних умов, пов'язаний відбір повинен швидше видаляти різноманітність у регіонах з низьким рівнем рекомбінація. Наприклад, рівень різноманітності Drosophila melanogaster значно нижчий в геномних областях з низькою рекомбінацією (див. Рис.\ ref {Fig:GW_HitchHiking_reduction}). Ця закономірність не може бути пояснена відмінностями в швидкості мутації між низькою та високою рекомбінацією областей, оскільки ця картина не спостерігається сильно в даних про розбіжність серед видів.
Ці закономірності можуть відображати дію селективних розгорток, що відбуваються повторювано вздовж генома. У наступному розділі ми представимо модель того, як рівень генетичного різноманіття повинен залежати від рекомбінації та щільності функціональних ділянок за моделлю рецидивуючих селективних розгорток. Однак інші форми пов'язаного відбору можуть впливати на генетичне різноманіття подібними способами. Наприклад, пов'язане генетичне різноманіття постійно втрачається від природних популяцій через видалення гаплотипів, які несуть згубні алелі; це називається моделлю «вибору фону». Нижче ми обговоримо модель вибору фону та її основні прогнози.
Більш загально, широкий спектр моделей відбору прогнозує видалення нейтрального різноманіття, пов'язаного з вибраними ділянками. Це пояснюється тим, що ефекти, що зменшують різноманітність високої дисперсії в репродуктивному успіху, посилюються протягом поколінь, коли існує спадкова дисперсія у фітнесі. Багато різних способів пов'язаного відбору, ймовірно, сприяють цим загальногеномним моделям різноманітності; нинішня проблема полягає в тому, як диференціювати ці різні режими.
Проста рецидивуюча модель селективних розгорток
Щоб пояснити, як постійний приплив розгортки може вплинути на рівні різноманітності, тут ми розробимо модель періодичних селективних розгорток.
Уявіть, що ми відбираємо пару нейтральних алелів у локусі на генетичній\(c\) відстані від локусу, де розгортки ініціюються всередині популяції з деякою дуже низькою швидкістю\(\nu\) на покоління. Час очікування між розгортками на нашому місці розподілено експоненціально\(\sim Exp(\nu)\) (див. Додаток до математики\ ref {eqn:exp_rv_def}). Кожна зачистка швидко проходить через популяцію в\(\tau\) поколіннях, так що кожна зачистка закінчується задовго до наступної зачистки (\(\tau \ll \frac{1}{\nu}\)).
Як і раніше, шанс того, що наша нейтральна лінія не зможе рекомбінувати з розгортки\(p_{NR}\), такий, що ймовірність того, що наша пара родовищ змушена злитися шляхом розгортки, є\(e^{-c \tau}\). Тому наші лінії мають дуже низьку ймовірність.
\[\nu e^{-c \tau}\]
змушеного зливатися за допомогою розгортки на покоління. Якщо наші лінії не зливаються через розгортку, вони зливаються з нейтральною швидкістю\(\frac{1}{2N}\) на покоління. Таким чином, середній час очікування до коалесцирующей події між нашою нейтральною парою ліній через розгортку або нейтральну коалесцирующую подію становить
\[\mathbb{E}(T_2) = \frac{1}{\nu e^{-c \tau} + \frac{1}{2N}}\]
Тепер уявіть, що розгортки не відбуваються у фіксованому місці по відношенню до нашого цікавого місця, але тепер відбуваються рівномірно випадково по всьому нашому геному. Підмітки ініціюються з дуже низькою швидкістю\(\nu_{BP}\) на базову пару на покоління. Швидкість коалесценції через розгортки в локусі\(\ell\) basepairs подалі від наших нейтральних локусів є\(2\nu_{BP} e^{-c_{BP} \ell \tau}\), де фактор двох походить від того, що основи можуть бути\(\ell\) basepars зліва або справа. Якщо наш нейтральний локус знаходиться посередині хромосоми, яка розтягує\(L\) базові пари в будь-якому напрямку, загальна швидкість розгортки на покоління, яка може змусити нашу пару ліній злитися, становить
\[2\int_0^{L} \nu_{BP} e^{-c_{BP} \ell \tau} d \ell = \frac{2\nu_{BP}}{c_{BP} \tau} \left(1-e^{-c_{BP} \tau L} \right)\]
так що якщо\(L\) дуже великий (\(c_{BP} \tau L \gg 1\)), швидкість коалесценції на покоління через розгортки є\(\frac{2\nu_{BP}}{c_{BP} \tau}\). Загальна швидкість коалесценції для пари ліній на покоління тоді
\[\frac{2\nu_{BP}}{c_{BP} \tau}+\frac{1}{2N}\]
Таким чином, наш середній час, поки пара родовищ об'єднається
\[\mathbb{E}(T_2) = \frac{1}{\frac{2\nu_{BP}}{c_{BP} \tau}+\frac{1}{2N}} = \frac{c_{BP}2N}{\frac{4N\nu_{BP}}{ \tau}+c_{BP}}\]
таким чином, що наше очікуване попарне різноманіття (\(\pi=2\mu\mathbb{E}(T_2)\)) у регіоні зі швидкістю рекомбінації\(r_{BP}\), яка переживає швидкість,\(\nu_{BP}\) є
\[\mathbb{E}(\pi) = \pi_0 \frac{c_{BP}}{\frac{4N\nu_{BP}}{ \tau}+c_{BP}} \label{eqn:pi_GW_HH}\]
де\(\pi_0\) наше очікуване різноманіття без будь-яких вибіркових розгорток, (\(pi_0=\theta=4N\mu\)). Очікувана різноманітність збільшується з тим\(c_{BP}\), як більш високі показники рекомбінації зменшують ймовірність нейтральних алелів автостопом разом із розгорткою і, таким чином, змушені зливатися шляхом розгортки. Очікувана різноманітність зменшується з\(\nu_{BP}\), оскільки більша щільність функціональних сайтів, що переживають розгортки, збільшує шанс бути пов'язаним з сусідньою розгорткою. Коли ми рухаємося до високого рівня\(c_{BP}\), припускаючи, що\(\nu_{BP}\) це не збільшується з\(c_{BP}\), наш рівень різноманітності повинен плато до того\(\theta\), щоб рівень генетичного різноманіття нейтральної ділянки повністю не пов'язаний з будь-якими вибраними локусами. Якщо ми припустимо, що наш геном відчуває постійну швидкість розгортання заданої сили, тобто\(\frac{4N\nu_{BP}}{ \tau}\) це константа, ми можемо відповідати варіації в\(\pi\) різних регіонах, які змінюються за швидкістю рекомбінації (\(c_{BP}\)), щоб оцінити швидкість популяції періодичні підмітання на одну базовупарі. Приклад пристосування цієї кривої до даних з Drosophila melanogaster наведено на малюнку\ ref {Fig:GW_HitchHiking_reduction}; див. ранній приклад пристосування подібної моделі повторного автостопа до таких даних. Параметр, який дає нам цю найкращу криву, є\(\frac{4N\nu_{BP}}{ \tau} \approx 7 \times 10^{-9}\). Маючи ефективний розмір населення мільйон і припускаючи, що підмітання займе тисячу поколінь, щоб досягти фіксації, ми вважаємо, що це означає\(\nu_{BP} \approx 10^{-12}\). Таким чином, дійсно низька швидкість помірно сильних розгорток, приблизно по одній кожній мегабазі на мільйон поколінь, - це все, що нам потрібно, щоб пояснити глибоке падіння різноманітності, яке спостерігається в регіонах генома з низькою рекомбінацією. Однак розгортки з позитивно відібраних алелів не є єдиною причиною загальногеномних сигналів пов'язаної селекції. Вибір проти шкідливих алелів також може керувати цими закономірностями.
Вибір фону
Популяції відчувають постійний приплив шкідливих мутацій у функціональні локуси, тоді як відбір діє для очищення їх від популяції, тим самим запобігаючи шкідливим заміщенням та підтримуючи функцію в цих локусах. Як ми обговорювали в розділі\ ref {Chapter:OneLocusSelection}, цей баланс між мутацією та відбором призводить до постійного рівня згубних змін у сукупності. Постійний відбір проти цієї згубної варіації впливає на різноманітність на пов'язаних сайтах. Кожна згубна мутація виникає навмання на гаплотипі в популяції, і оскільки виділення очищає цю мутацію, вона видаляє разом з нею будь-які нейтральні алелі, які також були на цьому гаплотипі. Це постійне видалення пов'язаних алелів з популяції діє на зменшення різноманітності в регіонах, що оточують функціональні локуси, ефект, відомий як вибір фону (BGS).
Яка частка наших гаплотипів вільна від згубних мутацій у будь-якому поколінні і так вільна, щоб сприяти майбутнім поколінням? Ну, при балансі мутації-відбору обмежений локус зі швидкістю мутації\(\mu\) до шкідливих алелів, які відчувають коефіцієнт відбору\(sh\) проти них у гетерозигот, призведе до\(\frac{\mu}{sh}\) хромосоми, що несуть згубний алель. Деякі з цих гаплотипів можуть бути передані наступному поколінню, але якщо вони повністю пов'язані з шкідливим локусом, вони всі зрештою будуть втрачені, оскільки вони несуть згубну мутацію на місці під обмеженням. Таким чином, для нейтрального поліморфізму, завершеного, пов'язаного з обмеженим локусом,\(2N(1-\frac{\mu}{sh})\) лише алелі отримують внесок майбутнім поколінням. Тому рівень попарного розмаїття у постійної популяції за рахунок БГС на такому локусі буде
\[\E[\pi] = 2 \mu \times 2N(1-\frac{\mu}{sh}) = \pi_0 (1-\frac{\mu}{sh})\]
де\(\pi_0= 4N\mu\), рівень нейтрального попарного різноманіття при відсутності пов'язаного відбору.
[Рис: BGS_мультфільм]
Ефекти фонового виділення більш виражені в областях низької рекомбінації, де нейтральні алелі менш здатні рекомбінуватися на тлі шкідливих алелів. Таким чином, під фоновим відбором ми також очікуємо зменшення різноманітності в регіонах нижчої рекомбінації.
Для нейтрального локусу, який є фракцією рекомбінації\(r\) далеко від локусу, що підлягає обмеженню, рівень різноманітності
\[\E[\pi] = \pi_0 \left(1-\frac{\mu sh}{2(c+sh)^2} \right) \label{eqn:pi_loc_BGS_1}\]
Коли ми віддаляємося від локусу, який відчуває очищаючий відбір, ми збільшуємося\(c\), і різноманітність повинна відновитися. Наприклад, віддаляючись від генних регіонів в геному кукурудзи, ми бачимо середній рівень відновлення різноманітності. Це відбувається як у кукурудзи, так і у теосінте, дикого прабатька кукурудзи. Зниження різноманітності навколо несинонімічних ділянок сильніше в теосінте, можливо, тому, що прискорений дрейф через вузьке місце в кукурудзі може дещо звільнити обмеження на ділянках, де дуже слабо шкідливі алелі відокремлені раніше при балансі мутації-селекції.
[Рис: BGS_кукурудза]
Більш загально, якщо нейтральний локус оточений\(L\) локусами, які відчувають очищення виділення на рекомбінаційних відстанях\(c_1,\cdots,c_L\), то складання Equation\ ref {eqn:pi_loc_bgs_1} через ці локуси, очікуване зменшення різноманітності приблизно
\[\E[\pi] = \pi_0 \prod_{i=1}^L \left(1-\frac{\mu sh}{2(c_L+sh)^2} \right) \approx \exp \left( \sum_{i=1}^L \frac{\mu sh}{2(c_i+sh)^2} \right) \label{eqn:pi_loc_BGS}\]
Для моделювання середнього нейтрального локусу в геномній області з заданою швидкістю рекомбінації ми можемо уявити, що наш нейтральний локус розташований у центрі великої області із загальною швидкістю рекомбінації\(C\) та загальною шкідливою швидкістю мутації\(U\), де\(U = \mu L\). Тоді наш вираз для різноманітності, Рівняння\ ref {EQN:PI_LOC_BGS}, просто
\[\E[\pi] \approx \pi_0 \exp \left( \frac{-U}{(sh+C)} \right) \approx \pi_0 \exp \left( \frac{-U}{C} \right). \label{eqn:GW_BGS_1}\]
У цьому останньому наближенні ми припускаємо, що ми дивимося на великий регіон, з\(C \gg sh\). Зауважте, що подібно до генетичного навантаження Equation\ ref {eqn:mut_load}, цей вираз залежить лише від загальної шкідливої швидкості мутації. Будь-яка залежність від коефіцієнта відбору випадає, оскільки слабо відібрані мутації відокремлюються в популяції на більш високих частотах, але також віддаляються від популяції повільніше, дозволяючи більшій частині генома рекомбінувати від згубного фону.
[Рис:GW_BGS_скорочення]
Для першого пристосування цього до загальногеномних даних, ми могли б подивитися на різноманітність вікон довжини\(W\) bp (як на рис.\ ref {Fig:GW_BGS_reduction}). Якщо припустити, що існує постійна швидкість згубної мутації на базову пару\(\mu_{BP}\), то\(U=\mu_{BP}W\). Крім того, якщо наше геномне вікно має швидкість рекомбінації\(c_{BP}\) на базову пару, наша загальна генетична довжина є\(R=c_{BP}W\). Роблячи ці заміни в Equation\ ref {EQN:GW_BGS_1}, наш розмір вікна скасовується, щоб дати
\[\E[\pi] \approx \pi_0 \exp \left(\frac{-\mu_{BP}}{c_{bp}} \right) \label{eqn:GW_BGS_2}\]
Дивлячись на вікна, які змінюються за швидкістю рекомбінації\(c_{BP}\), тобто ми можемо встановити Equation\ ref {EQN:GW_BGS_2} до даних для оцінки\(\mu_{BP}\). Приклад виконання цього з даними D. melanogaster наведено на малюнку\ ref {Fig:GW_BGS_reduction}, що дає оцінку шкідливої швидкості мутації\(\mu_{BP}\approx 3.2 \times 10^{-9}\). Це приблизно в тому ж порядку, що і швидкість мутації на базову пару в D. melanogaster, і тому ця шкідлива оцінка швидкості мутації дещо висока, оскільки це вимагатиме обмеження більшої частини генома, але як перше наближення це не страшно. Зверніть увагу, наскільки схожа на модель автостопа, припускаючи, що деяке поєднання BGS та автостопом може пояснити широку залежність між різноманітністю та рекомбінацією, що спостерігається у D. melanogaster та інших видів.
[Рис: Маквікер_BGS]
Оскільки наші анотації функціональних областей генома покращилися, так і наші методи, щоб зробити висновок про вибір фону. Більш сувора версія цього аналізу сьогодні включала б зміну щільності кодування серед вікон у параметр\(\mu_{BP}\). Завдяки детальним геномним анотаціям, що показують області кодування та обмежені області, які не кодують, ми також можемо вийти за рамки простого аналізу широкомасштабних моделей. Наприклад, встановіть модель вибору фону до передбачувано нейтральної попарної різноманітності вздовж генома людини, використовуючи Equation\ ref {Eqn:pi_loc_bgs} для оцінки ефекту BGS на кожному локусі, зважуючи генетичну відстань до всіх навколишніх областей кодування та обмежених некодуючих сайтів. Це дозволило оцінити частоту мутації та середні коефіцієнти відбору, що діють проти згубних алелів у цих областях генома. Ця найкраща модель також дозволила їм прогнозувати рівні різноманітності вздовж генома, розріз якого показаний на малюнку\ ref {Fig:McVicker_bgs}. Таким чином, широкомасштабні особливості поліморфізму вздовж генома добре описуються фоновим виділенням (або зв'язаним виділенням в цілому).
Згубні показники мутації, оцінені шляхом встановлення моделі BGS, знову були занадто високими, як у прикладі Drosphila вище, припускаючи, що лише BGS недостатньо, щоб пояснити весь ефект пов'язаного відбору. Але як тоді ми йдемо про розрізнення впливу BGS від автостопом?
Відрізнення впливу автостопа від фонового відбору в загальногеномних даних
Різноманітні підходи були прийняті, щоб почати відокремити наслідки автостопом від вибору фону. Значна частина найсильніших доказів, що показують наслідки обох, походить від Drosophila melanogaster, і ми переглядаємо деякі з цих доказів тут. Очікується, що автостоп матиме систематичний вплив на спектр частот нейтральної ділянки, спотворюючи його до рідкісних незначних алелів (відображаючи повільне відновлення різноманітності після розгортки). Тому слід очікувати спотворення зведеної статистики, такої як D Tajima в регіонах з низькою рекомбінацією, якщо автостоп сприяє зменшенню різноманітності в цих регіонах. У D. melanogaster спостерігається більший перекіс у бік рідкісних алелів на передбачувано нейтральних ділянках у регіонах низької рекомбінації; див. Ліву панель рисунка\ ref {fig:tajimas_d_dn_pi}. Однак, хоча цей перекос не очікується за простих моделей сильного вибору фону.
[Рис.: Таджімас_д_д_Пі]
Ще одне передбачення моделі автостопа, де алель підмітає до фіксації, полягає в тому, що має бути функціональна заміна, пов'язана з кожною розгорткою. Або, щоб перевернути це навколо, ми могли б очікувати, щоб побачити більший вплив автостопом, де є більш функціональні заміни. Наприклад, регіони, що оточують несинонімічні заміни, повинні мати нижчий рівень різноманітності, якщо висока частка несинонімічних замін є адаптивною. Знову ж таки, ця закономірність видно в D. melanogaster.
[Рис: Єляшів_навколо_subs]
Просуваючи цю ідею далі, ми можемо подивитися на падіння різноманітності, що оточує несинонімічну заміну, усереднену по всіх замінах геному. виявили сильніше падіння в різноманітності навколо несинонімічних замін, ніж синонімічні заміни. Розширюючи модель, щоб відповідати моделі вибору фону та автостопом до передбачуваної нейтральної різноманітності вздовж генома, вони виявили, що падіння різноманітності навколо синонімічних замін походить здебільшого від BGS. Але щоб повністю пояснити падіння різноманітності навколо несинонімічних замін, розумна частка цих несинонімічних замін повинна супроводжуватися класичною (жорсткою) розгорткою. Більшість цих розгорток, за оцінками, пов'язані з дуже слабким відбором, з коефіцієнтами відбору\(<10^{-4}\). Крім того, оцінено\(77\)\(89\%\) зменшення нейтрального різноманіття за рахунок відбору на пов'язаних сайтах, і дійшли висновку, що жодне геномне вікно не було повністю вільним від наслідків відбору. Таким чином пов'язаний відбір має глибокий ефект у деяких видів, таких як Drosophila melanogaster.
Додаток. Імовірність не рекомбінувати обраний гаплотип під час розгортки.
Ми знаємо, що в наші дні наша нейтральна лінія пов'язана з вибраним алелем. Імовірність того, що наше походження в деякому\(t\) поколінні в часі знаходиться в гетерозиготі\(1-X(t)\), є, і ймовірність того, що рекомбінація відбувається у цієї людини, є\(r\). Отже, ймовірність того, що наша нейтральна лінія походить від рекомбінантного гаплотипу\(t\) поколінь назад, є
\[c (1-X(t))\]
Таким чином, ймовірність (\(p_{NR}\)) того, що наша лінія не походить від рекомбінантного гаплотипу від події рекомбінації в\(\tau\) поколіннях, яким потрібен наш обраний аллель для переміщення по популяції, є
\[p_{NR}=\prod_{t=1}^{\tau} \big(1- c(1-X(j))\big)\]
Якщо припустити,\(c\) що мало, то\(\left(1- c(1-X(t))\right) \approx e^{-r(1-X(t))}\), такий, що
\[p_{NR}=\prod_{t=1}^{\tau} \left(1- c(1-X(t))\right) \approx \exp \left( -c\sum_{t=1}^{\tau} 1- X(t) \right) =\exp \left( -c \tau (1-\widehat{X}) \right)\]
де\(\widehat{X}\) середня частота похідного корисного алеля через його траєкторію, коли він змітає по частоті,\(\widehat{X} = \frac{1}{\tau} \sum_{t=1}^{\tau} X(t)\). Оскільки наш алель є адитивним, його траєкторія для частот\(<0.5\) - це дзеркальне відображення його траєкторії для частот\(>0.5\), отже, середньої частоти\(\widehat{X} =0.5\). Це спрощує наше вираження
\[p_{NR} = e^{-c \tau/2 }.\]
Коли спочатку рідкісний обраний алель змітає по частоті, він несе з собою генетичний фон (гаплотип), на якому він виник. Алелі, яким пощастило подорожувати автостопом разом з обраним алелем, перетягуються на високу частоту і різноманітність виснажується цим ефектом автостопа.
У рекомбінуючих регіонах різноманітність лише локально пригнічується селективною розгорткою, оскільки далі від обраної ділянки алелі можуть рекомбінувати вкл/викл розгортки, дозволяючи різноманітності зберігатися в популяції. Геномна шкала ефекту автостопа лінійно залежить від часу, який потрібен вибраний алель для проходу по популяції та обернено від місцевої швидкості рекомбінації. Характерне падіння різноманітності використовується для пошуку селективних розгорток у скануванні геному та оцінки термінів та сили відбору.
Селективні розгортки залишають цілий ряд інших геномних сигналів, які були використані для їх ідентифікації, включаючи спотворення частотного спектра (більш екстремальний перекіс до рідкісних алелів) та підвищені\(F_{ST}\) між популяціями.
Ми бачимо зменшення різноманітності в регіонах з низькою рекомбінацією, що відповідає більшому видаленню різноманітності в цих регіонах через повторювані автостопом. Однак цей ефект у масштабі генома також узгоджується з фоновим відбором, видаленням пов'язаного різноманіття разом із згубними алелями.
[Мал.: розгалужений_теосінте]
Сучасна кукурудза, отримана з теосінте, бур'яної рослини, яка росте в Південній і Центральній Америці. Вражаюча фенотипічна відмінність між теосінтом і кукурудзою полягає в тому, що теосінт - кущиста рослина, тоді як кукурудза росте переважно вгору. Один ген, який був залучений до цієї трансформації, - це tb1. секвенував область навколо цього гена, щоб виявити, що фонові рівні нейтрального різноманіття знижуються навколо цього гена.
A) Це займає приблизно 300bp для різноманітності, щоб відновити віддаляючись від розгортки. оцінка\(r = 4 \times 10^{-7}\) на базову пару. Оцініть час (у роках) з моменту виникнення обраного варіанту кукурудзи tb1 як нова мутація. Кукурудза є однорічною рослиною, тому припускають 1 покоління на рік.
Б) Припустимо, що ефективний розмір цього диплоїдного населення є\(N = 10^6\). Який селективний коефіцієнт цього аллеля tb1?