Стохастична втрата сильно відібраних алелів

Навіть сильно корисні алелі можуть бути втрачені від популяції, коли вони досить рідкісні. Це пояснюється тим, що кількість потомства, залишеного особинами наступному поколінню, в корені стохастично. Коефіцієнт відбору s =\(1\%\) є сильним коефіцієнтом відбору, який може проганяти алель через популяції за кілька сотень поколінь після встановлення алеля. Однак, якщо особини мають в середньому невелику кількість потомства на покоління, перша особина, яка несе наш корисний алель, у якого в середньому\(1\%\) більше дітей, ніж їх однолітки, може легко мати нульового потомства, що призведе до втрати нашого алелю, перш ніж він коли-небудь отримає шанс поширення.

Щоб зробити перший удар у цій проблемі, давайте подумаємо про дуже велику гаплоїдну популяцію, в якій одна людина починається з обраного аллеля, і запитати про ймовірність можливої втрати нашого обраного алеля, починаючи з цього єдиного екземпляра. Щоб вивести цю ймовірність loss (\(p_L\)), ми скористаємося простим аргументом. Наш обраний алель буде врешті-решт втрачений з популяції, якщо кожна людина з алелем не зможе залишити нащадків.

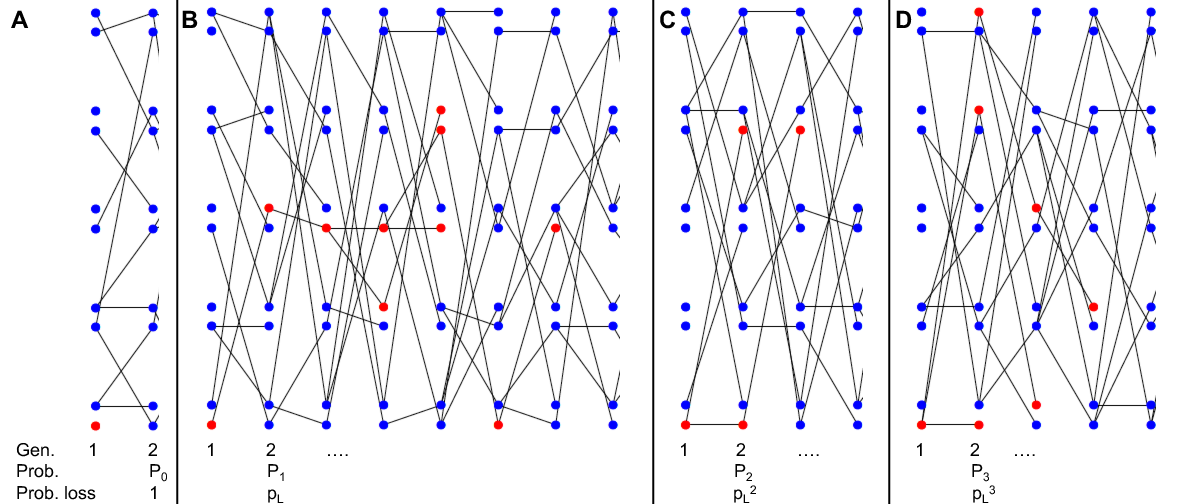
Що ж, ми можемо думати про різні випадки:

1. У нашому першому поколінні, ймовірно,\(P_0\) наш індивідуальний алель не залишає жодних копій себе наступному поколінню, і в цьому випадку наш алель втрачається (рис.\(\PageIndex{1}\) А).
2. Як варіант, наш алель може залишити одну копію себе наступному поколінню (з ймовірністю\(P_1\)), і в цьому випадку з ймовірністю\(p_L\) ця копія в кінцевому підсумку згасне (рис.\(\PageIndex{1}\) B).
3. Наш алель міг би залишити дві копії себе наступному поколінню (з ймовірністю\(P_2\)), і в цьому випадку з ймовірністю\(p_L^2\) обидві ці копії в кінцевому підсумку зникнуть (рис.\(\PageIndex{1}\) С).
4. Більш загально, наш алель може залишити може залишити\(k\) копії (\(k>0\)) самого себе наступному поколінню (з ймовірністю\(P_k\)), і в цьому випадку з ймовірністю\(p_L^k\) всі ці копії в кінцевому підсумку зникнуть (наприклад, рис.\(\PageIndex{1}\) D).

Підсумовуючи ці ймовірності, ми бачимо, що

\[p_L = \sum_{k=0}^{\infty} P_k p_L^{k}\]

Тепер нам потрібно буде вказати\(P_k\), ймовірність того, що особина, яка несе наш обраний аллель, має\(k\) потомство. Для того щоб ця популяція залишалася постійною в розмірах, ми будемо вважати, що особини без обраної мутації мають в середньому одне потомство на покоління, тоді як особини з нашим обраним алелем мають в середньому\(1+s\) потомство на покоління. Ми припустимо, що кількість потомства, яке має індивід, є Пуассоном, розподіленим із середнім\(1\) значенням\(1+s\), заданим або, тобто ймовірність того, що особа з вибраним аллелем має\(i\) дітей, становить

\[P_i= \frac{(1+s)^i e^{-(1+s)}}{i!}\]

Підставляючи\(P_k\) в рівняння вище, бачимо

\[\begin{aligned} p_L &= \sum_{k=0}^{\infty} \frac{(1+s)^ke^{-(1+s)}}{k!} p_L^{k} \nonumber \\ &= e^{-(1+s)} \left( \sum_{k=0}^{\infty} \frac{\left(p_L(1+s) \right)^k}{k!} \right)\end{aligned}\]

Термін в дужках сам по собі є експоненціальним розширенням, тому ми можемо переписати це рівняння як

\[p_L = e^{(1+s)(p_L-1)} \label{prob_loss}\]

Рішення для\(p_L\) дасть нам нашу ймовірність втрати для будь-якого коефіцієнта відбору. Давайте перепишемо наш результат з точки зору ймовірності уникнути втрати,\(p_F = 1-p_L\). Ми можемо переписати рівняння\ ref {prob_loss} як

\[1-p_F = e^{-p_F(1+s)}\]

\[1-p_F \approx 1-p_F(1+s)+p_F^2(1+s)^2/2\]

Вирішуючи це, ми виявляємо, що

\[p_F = 2s. \label{eqn:prob_fix_strong}\]

Таким чином, навіть алель з коефіцієнтом\(1\%\) відбору має\(98\%\) ймовірність втратити при першому введенні в популяції шляхом мутації.

Якщо швидкість мутації до нашого вигідного алелю є\(\mu\), і є\(N\) особини в нашій гаплоїдної популяції, то\(N \mu\) вигідні мутації виникають на покоління. Кожна з цих нових корисних мутацій має ймовірність\(p_F\) закріплення. Таким чином, кількість вигідних мутацій, що виникають на покоління, які в кінцевому підсумку зафіксуються в популяції\(N \mu p_F\), є, і час очікування мутації, яка буде фіксувати виникати, є відповідним цьому:\(\frac{1}{N\mu p_F}\). Таким чином, при адаптації до нового тиску селекції за допомогою нових мутацій, чисельності популяції, мутаційного цільового розміру та вибіркової переваги нових мутацій все має значення. Однією з причин, чому комбінації препаратів використовуються проти таких вірусів, як ВІЛ та малярія, є те, що, навіть якщо віруси адаптуються до одного з препаратів, вірусне навантаження (\(N\)) пацієнта значно знижується, що робить малоймовірним, що населенню вдасться виправити другий лікарський резистентний алель.

Диплоїдна модель стохастичної втрати сильно відібраних алелів.

Ми також можемо адаптувати цей результат до диплоїдної обстановки. Якщо припустити, що гетерозиготи\(1\) для алеля мають в середньому\(1+hs\) діти, ймовірність\(1\) алель не втрачається, починаючи від одиничного екземпляра в популяції, становить

\[p_F = 2 h s \label{eqn:diploid_escape}\]

для\(h>0\). Зверніть увагу, що це дещо інша параметризація від нашої диплоїдної моделі в попередньому розділі; ось домінування нашого позитивно підібраного алеля,\(h\) що\(h=1\) відповідає повній селективній перевазі, вираженій у індивіда з лише єдиним екземпляром. Таким чином, ймовірність того, що корисний алель не втрачається, залежить лише від відносної переваги придатності гетерозиготи; це тому, що коли аллель рідкісний, він зазвичай присутній у гетерозигот, і тому його ймовірність уникнути втрати просто залежить від придатності цих людей порівняно з гомозиготи для родового алеля (припускаючи безпородну популяцію).

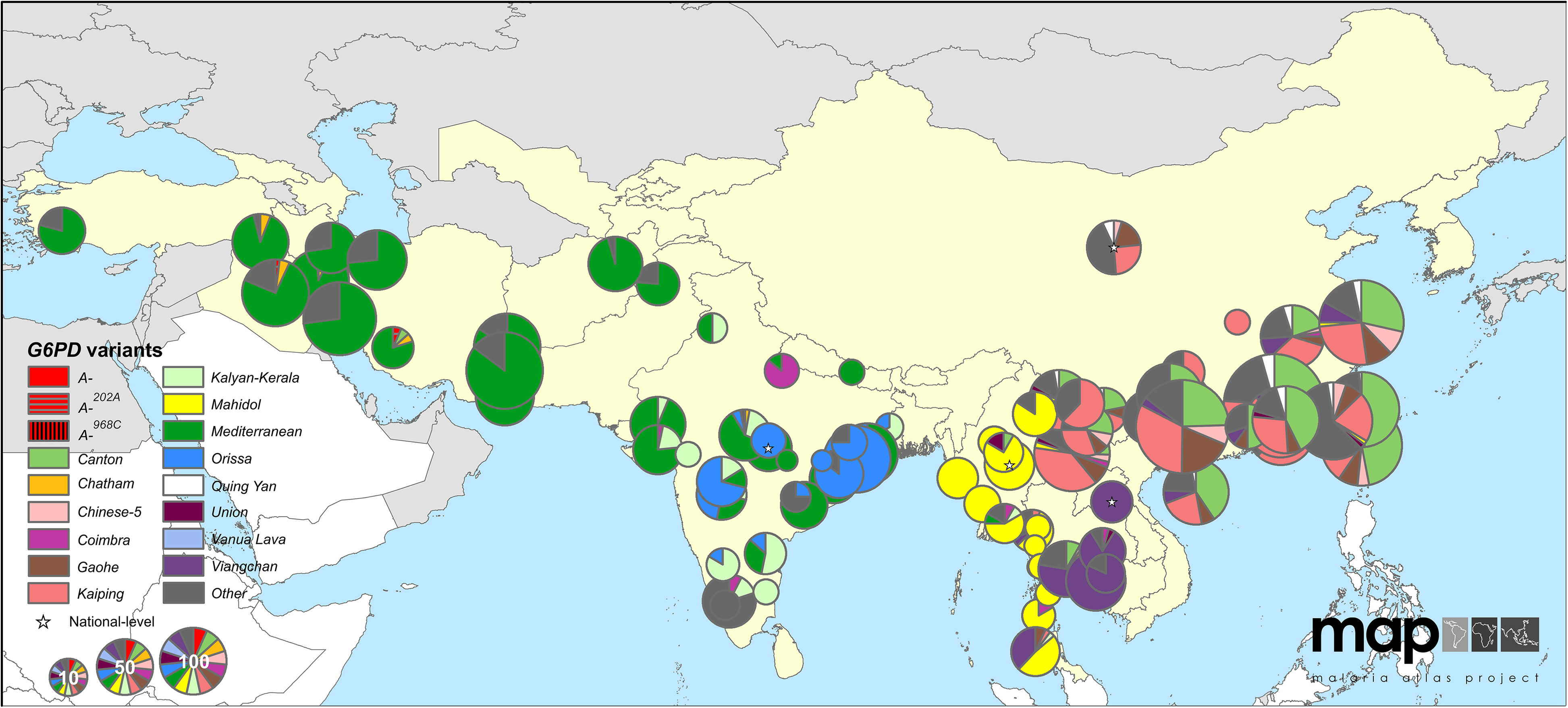
Приблизно за останні десять тисяч років адаптивні алелі, що надають стійкість до малярії, виникли в ряді генів і поширилися через людські популяції в районах, де малярія є ендемічною. Одним з особливо вражаючих випадків конвергентної еволюції у відповідь на тиск селекції, що накладається малярією, є численні зміни по всьому гену G6PD, які включають щонайменше 15 поширених варіантів лише в Центральній та Східній Азії, які знижують активність ферменту. Ці алелі зараз зустрічаються з комбінованою частотою близько 8% частоти в ендемічних малярією районах, рідко перевищуючи 20%. Чи всі ці варіанти надають стійкість до малярії, невідомо, але ряд цих алелів продемонстрували вплив проти малярії і, як вважають, мають вибіркову перевагу перед гетерозиготами,\(sh > 5\%\) де малярія є ендемічною.

Маючи 5% перевагу у гетерозигот, алель G6PD, присутній як єдиний екземпляр, матиме лише 10% ймовірність фіксації в популяції. Якщо це так, то чому адаптація малярії неодноразово відбувалася через зміни на G6PD? Ну, можливо, адаптація не почалася з єдиної копії вибраного аллеля. Скільки копій алелів дефіциту G6PD, як ми очікуємо, були сегрегації в популяції до зміни тиску на відбір?

За відсутності малярії ці алелі G6PD є шкідливими для носіїв, які страждають на дефіцит G6PD, що призводить до гемолітичної анемії, коли люди піддаються впливу різних сполук, особливо тих, що присутні в бобах фави. Там вище ста баз, де можуть виникати алелі дефіциту G6PD, тому, припускаючи швидкість мутації\(\approx 10^{-8}\) на базову пару на покоління, ми можемо приблизно оцінити швидкість мутацій, що виникають, які впливають на ген G6PD\(\mu \approx 10^{-6}\) відповідно до покоління. За відсутності малярії селективна вартість того, щоб бути носієм гетерозигот алеля з дефіцитом G6PD, повинна була бути на порядку\(5\%\) або більше, і, таким чином, частота алеля при балансі мутації-відбору була б\(\approx \frac{10^{-6}}{0.05} =2 \times 10^{-5}\). Припускаючи ефективну чисельність населення\(2-20\) мільйона осіб, приблизно п'ять-десять тисяч років тому це означає, що було б сорок-чотириста копій алелю дефіциту G6PD, присутніх у популяції, коли тиск на відбір змістився при введенні малярії. Шанс того, що один з цих нових адаптивних алелів втрачається, є,\(90\%\) але шанс, що вони всі втрачені\(<(0.9)^{40}\approx 0.02\), є, тобто було б більше\(98\%\) шансів, що адаптація відбудеться через один або кілька алелів на G6PD . Скільки алелів би уникнути дрейфу? Ну, з\(40 - 400\) копіями алелів перед малярією, і кожен з них має\(10\%\) ймовірність уникнути дрейфу, ми очікуємо, що між алелями\(40\) G6PD\(4\) і G6PD уникнути дрейфу і сприяти адаптації . Ми бачимо\(15\) загальні алелі G6PD в Євразії, тому наша проста модель адаптації з балансу мутації-селекції здається розумною.

Вправа\(\PageIndex{1}\)

«Сито Халдейна» - це назва ідеї про те, що мутації, які сприяють адаптації, швидше за все, будуть домінуючими або принаймні домінуючими.

1. Коротко поясніть цей аргумент словесною моделлю, що стосується результатів, які ми розробили в останніх двох розділах.
2. Вважається, що сито Халдейна менш важливо для адаптації від раніше згубної стоячої варіації, ніж адаптація від нової мутації. Чи можете ви пояснити інтуїцію, що стоїть за цією ідеєю?
3. Сито Халдейна, ймовірно, буде менш важливим у інбредних, наприклад, самоврядуваннях, популяціях. Чому це?

Взаємодія між генетичним дрейфом і слабким відбором

Для сильно відібраних алелів, як тільки алель уникнув початкових втрат на низьких частотах, його шлях буде детерміновано визначатися його коефіцієнтами вибору. Однак, якщо селекція слабка порівняно з генетичним дрейфом, стохастичність відтворення може відігравати певну роль у траєкторії, яку приймає алель, навіть коли вона поширена у популяції. Якщо відбір є досить слабким порівняно з генетичним дрейфом, то генетичний дрейф буде домінувати в динаміці алелей, і вони будуть вести себе так, ніби вони ефективно нейтральні. Таким чином, ступінь, в якій відбір може формувати закономірності молекулярної еволюції, буде залежати від відносних сильних сторін відбору та генетичного дрейфу. Але наскільки слабким повинен бути вибір на алелі для дрейфу, щоб пересилити вибір? І чи мають ці взаємодії між відбором та дрейфом довгострокові наслідки для еволюції загальногеномних моделей?

Для моделювання вибору та дрейфу кожного покоління ми можемо спочатку обчислити детерміновану зміну частоти алелів через вибір за допомогою нашої детермінованої формули. Потім, використовуючи нашу нещодавно розраховану очікувану частоту алелів, ми можемо біноміально вибірку двох алелів для кожного нашого потомства, щоб побудувати наступне покоління. Такий підхід до спільного моделювання генетичного дрейфу і селекції називається моделлю Райта-Фішера.

За моделлю Райта-Фішера ми обчислимо очікувану зміну частоти алелів через вибір та дисперсію навколо цього очікування через дрейф. Щоб зробити наші розрахунки простіше, припустимо адитивну модель\(h=1/2\),\(s \ll 1\) т\(\overline{w} \approx 1\). Е. Використовуючи нашу детерміновану модель спрямованого вибору, з Chapter\ ref {chapter:OneLocusSelection}, і ці наближення дають нам детерміновані зміни внаслідок вибору

\[\Delta_S p = \mathbb{E}(\Delta p) = \frac{s}{2} p(1-p) \label{eqn:WF_mean}\]

Щоб отримати нашу нову частоту в наступному поколінні\(p_1\), ми біноміально вибірки з нашої нової детермінованої частоти\(p^{\prime}= p + \Delta_S p\), тому дисперсія в нашій частоті алелів змінюється від одного покоління до наступного задається

\[Var(\Delta p) = Var(p_1 - p) = Var(p_1) = \frac{p^{\prime}(1-p^{\prime})}{2N} \approx \frac{p(1-p)}{2N}. \label{eqn:WF_var}\]

де попередня частота алелів\(p\) випадає, оскільки вона є постійною, і дисперсія в нашій новій частоті алелів випливає з того факту, що ми біноміально відбираємо\(2N\) нові алелі з частоти,\(p^{\prime}\) щоб сформувати наступне покоління.

Щоб отримати наш перший погляд на відносні ефекти відбору проти дрейфу, ми можемо просто подивитися, коли наша зміна частоти алелів, спричинена відбором в межах покоління, досить сумлінно передається через покоління. Зокрема, якщо наша очікувана зміна частоти алелів набагато більша, ніж дисперсія навколо цієї зміни, генетичний дрейф відіграватиме невелику роль у долі нашого обраного алеля (як тільки аллель не має низького числа копій у популяції). Коли відбувається селекція домінантний генетичний дрейф? Це станеться\(\mathbb{E}(\Delta p) \gg Var(\Delta p)\), якщо, тобто коли\(|Ns| \gg 1\). І навпаки, будь-яка надія на обраний нами алель після його детермінованого шляху буде швидко скасована, якщо наша зміна частот алелів через вибір набагато менше, ніж дисперсія, викликана дрейфом. Отже, якщо абсолютне значення нашого масштабованого коефіцієнта відбору чисельності населення\(| Ns| \ll 1\), то дрейф буде домінувати над долею нашого алеля.

Для подальшого прогресу в розумінні долі алелей з коефіцієнтами відбору порядку\(\frac{1}{N}\) потрібно більш ретельне моделювання. Однак за нашою диплоїдною моделлю, з коефіцієнтом адитивного відбору\(s\), ми можемо отримати ймовірність того, що алель\(1\) фіксується всередині популяції, починаючи з частоти\(p\):

\[p_F(p) = \frac{1-e^{-2Ns p }}{1-e^{-2Ns}} \label{eqn:prob_fixed}\]

Доказ цього результату наведено нижче (див. Розділ 1.1). Новий алель, який надходить в популяції з частотою,\(p=1/(2N)\) має ймовірність досягнення фіксації

\[p_F \left(\frac{1}{2N} \right) = \frac{1-e^{-s }}{1-e^{-2Ns}} \label{eqn:new_mut_prob_fixed}\]

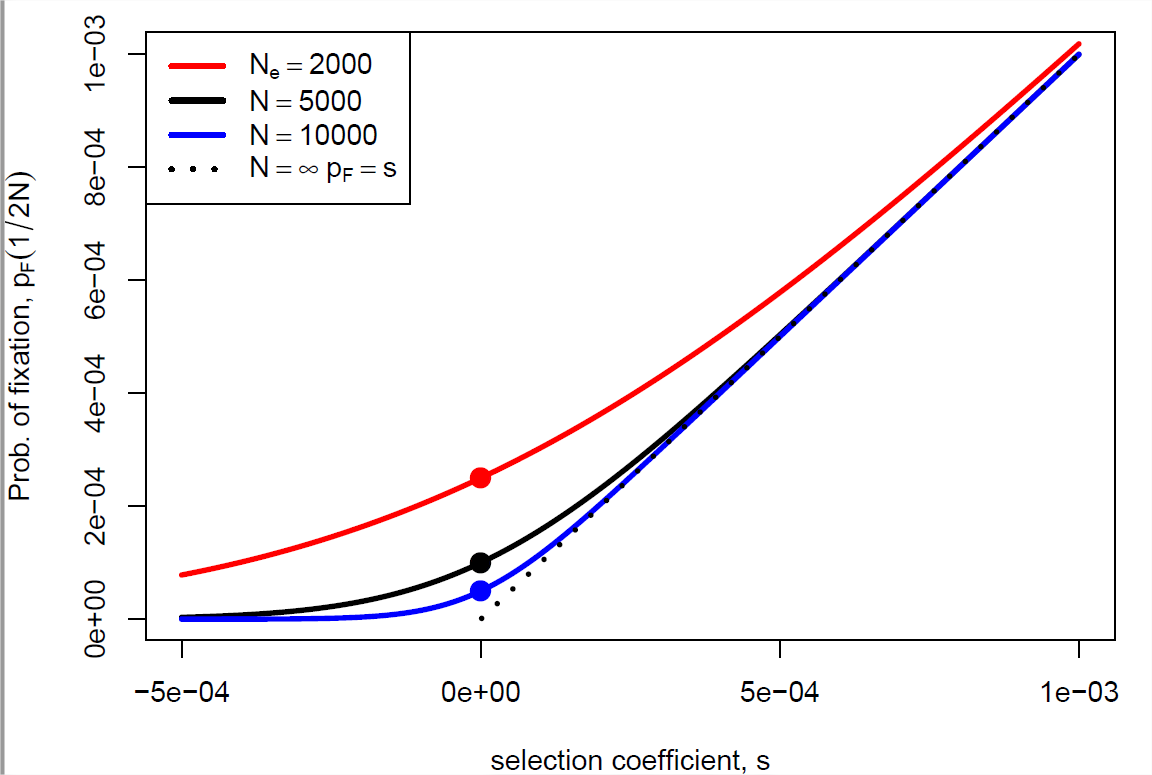
Якщо\(s \ll1\) але\(Ns \gg 1\) тоді\(p_F(\frac{1}{2N}) \approx s\), що чудово повертає нам результат, який ми отримали вище для алеля при сильному відборі (Equation\ ref {eqn:diploid_escape}). Наша ймовірність фіксації (Equation\ ref {eqn:new_mut_prob_fixed}) побудована як функція\(s\) і\(N\) на рис\(\PageIndex{7}\). Щоб відновити наш нейтральний результат, ми можемо взяти межу,\(s \rightarrow 0\) щоб отримати нашу нейтральну ймовірність фіксації\(\frac{1}{2N}\).

У разі, коли\(Ns\) знаходиться близько до\(1\), то

\[p_F \left( \frac{1}{2N} \right) \approx \frac{s}{1-e^{-2Ns}} \label{eqn:escape_from_intro}\]

Це більше, ніж наш попередній результат\(p_F=s\) від аргументу процесу розгалуження (використовуючи нашу адитивну модель\(h=1/2\)), все частіше для менших\(N\). Чому це? Ну, у меншій популяції нова мутація починається з більш високою частотою (\(\frac{1}{2N}\)), ніж у більшої популяції, це дає початковий поштовх вибраному алелю в менших популяціях.

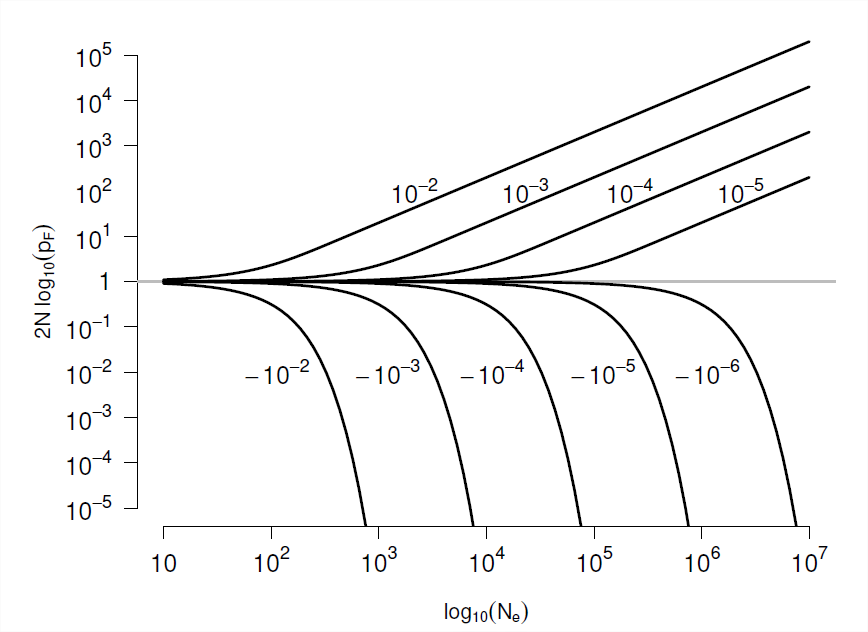
Якщо для вибору працювати на алелі, нам потрібен коефіцієнт відбору, щоб задовольнити\(|Ns|\gg 1\), то, що тримає, якщо\(|s|\gg \frac{1}{N}\). Ну, ефективні розміри населення часто досить великі, на порядку сотень тисяч або мільйонів людей, таким чином, коефіцієнти відбору на порядку\(10^{-5}\) до\(10^{-6}\) можуть бути ефективно обрані на, вони представляють неймовірно незначні (дис) переваги з точки зору кількості потомства, яке вони залишають наступному поколінню (див. Малюнок\(\PageIndex{8}\)). Хоча ми не в змозі виявити вимірювання всіх, крім великих розмірів фітнес-ефекту, за винятком деяких елегантних експериментів (наприклад, у мікробів), такі малі ефекти видно для виділення у великих популяціях. Таким чином, якщо послідовний тиск відбору чиниться протягом тривалих періодів часу, природний відбір може потенційно тонко налаштувати різні аспекти організму.

Як один із прикладів цієї тонкої настройки, розглянемо, наскільки ретельно розроблена та оптимізована послідовність кодонів для перекладу. Через переродження білкового коду кілька кодонів кодують одну і ту ж амінокислоту. Наприклад, існує шість різних кодонів, які можуть кодувати лейцин. Хоча ці синонімічні кодони еквівалентні на рівні білка, клітини відрізняються кількістю молекул тРНК, які пов'язують ці кодони, і тому ефективністю та точністю, з якою білки можуть утворюватися шляхом перекладу та складання. Ці незначні відмінності в швидкості перекладу, ймовірно, часто відповідають крихітним відмінностям у придатності, але чи мають вони значення?

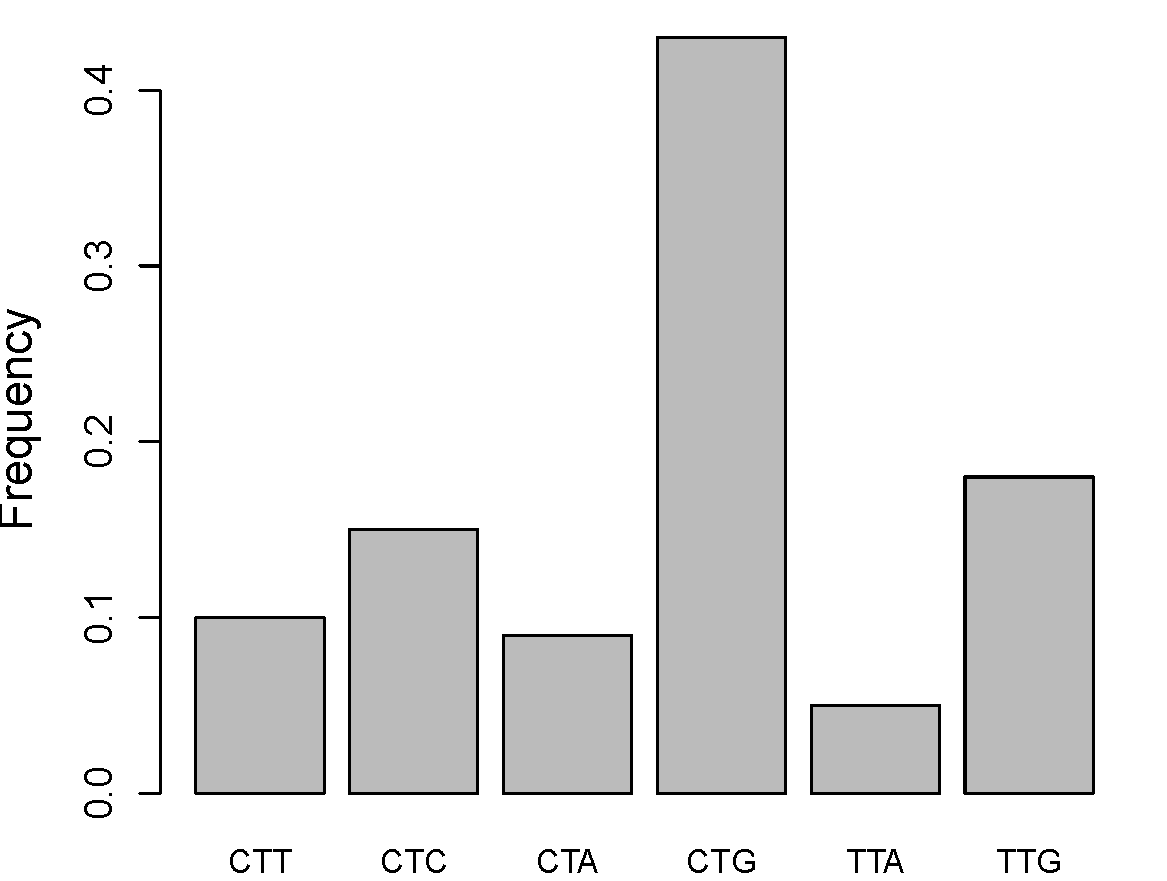
У багатьох організмах існує сильне зміщення кодонів для кодування певних амінокислот, див. Рис.\ ref {Fig:Leucine}, причому найпоширеніший кодон відповідає найбільш поширеній тРНК у клітині. Цей «кодоновий ухил», ймовірно, відображає комбіновану дію слабкого відбору та мутаційного тиску, підштовхуючи кодоновий склад достатку генома та тРНК до адаптивного компромісу. Ці тиск на відбір діяли протягом довгих періодів часу, оскільки моделі використання кодонів часто дуже схожі для видів, які розходилися протягом багатьох десятків мільйонів років тому. Порівняно з іншими генами, високовиражені гени демонструють сильний ухил до використання кодонів, що відповідають рясним ТРНК, що відповідає думці про те, що синонімічний вміст кодонів високоекспресованих генів розвивається для оптимізації їх перекладу (див. Рисунок\ ref {fig:gene_expression_codon_bias} для раннього прикладу). Ці моделі, ймовірно, представляють дію тиску на відбір, які в середньому неймовірно слабкі, але які грали протягом величезних часових періодів.

Фіксація злегка згубних алелей

З малюнка\(\PageIndex{7}\) ми бачимо, що слабо згубні алелі також можуть фіксуватися, особливо в невеликих популяціях. Щоб зрозуміти, наскільки ймовірно, що згубні алелі випадково досягають фіксації генетичним дрейфом, припустимо диплоїдну модель з адитивним відбором (з коефіцієнтом відбору\(-s\) проти нашого алелю\(2\)).

Якщо\(N s \gg 1\) тоді наш згубний алель (алель\(2\)) не може досягти фіксації. Однак якщо\(Ns\) не велика, то ймовірність фіксації

\[p_F \left( \frac{1}{2N} \right) \approx \frac{s}{e^{2Ns}-1} \label{eqn:fix_deleterious}\]

для нашого одноразового згубного алелю. Тож згубні алелі можуть фіксуватися всередині популяцій (хоча і з низькою швидкістю),\(Ns\) якщо вони не надто великі. Як вище, це пов'язано з тим, що хоча згубні мутації ніколи не уникнуть втрат у нескінченних популяціях, вони можуть закріпитися в кінцевій популяції, досягнувши\(2N\) копій.

Вправа\(\PageIndex{2}\)

Виникає адитивна мутація, яка знижує відносну придатність гетерозигот\(10^{-5}\). Яка ймовірність того, що ця мутація фіксується у диплоїдної популяції з ефективним розміром\(10^4\)? Яку ймовірність вона фіксує в популяції ефективного розміру\(10^6\)? Порівнюючи обидва з їх нейтральною ймовірністю, опишіть інтуїцію, що стоїть за цим результатом.

OHTA запропонував «майже нейтральну» теорію молекулярної еволюції в серії робіт. Вона припустила, що розумна частка знову виникаючих функціональних мутацій може мати дуже слабкі коефіцієнти відбору, так що види з меншими ефективними розмірами популяцій можуть мати більш високі показники фіксації цих дуже слабо згубних алелів. По суті, її припущення полягає в тому, що параметр\(C\) обмеження функціональної області не є фіксованою властивістю, а скоріше залежить від здатності населення протистояти припливу дуже слабо згубних мутацій.

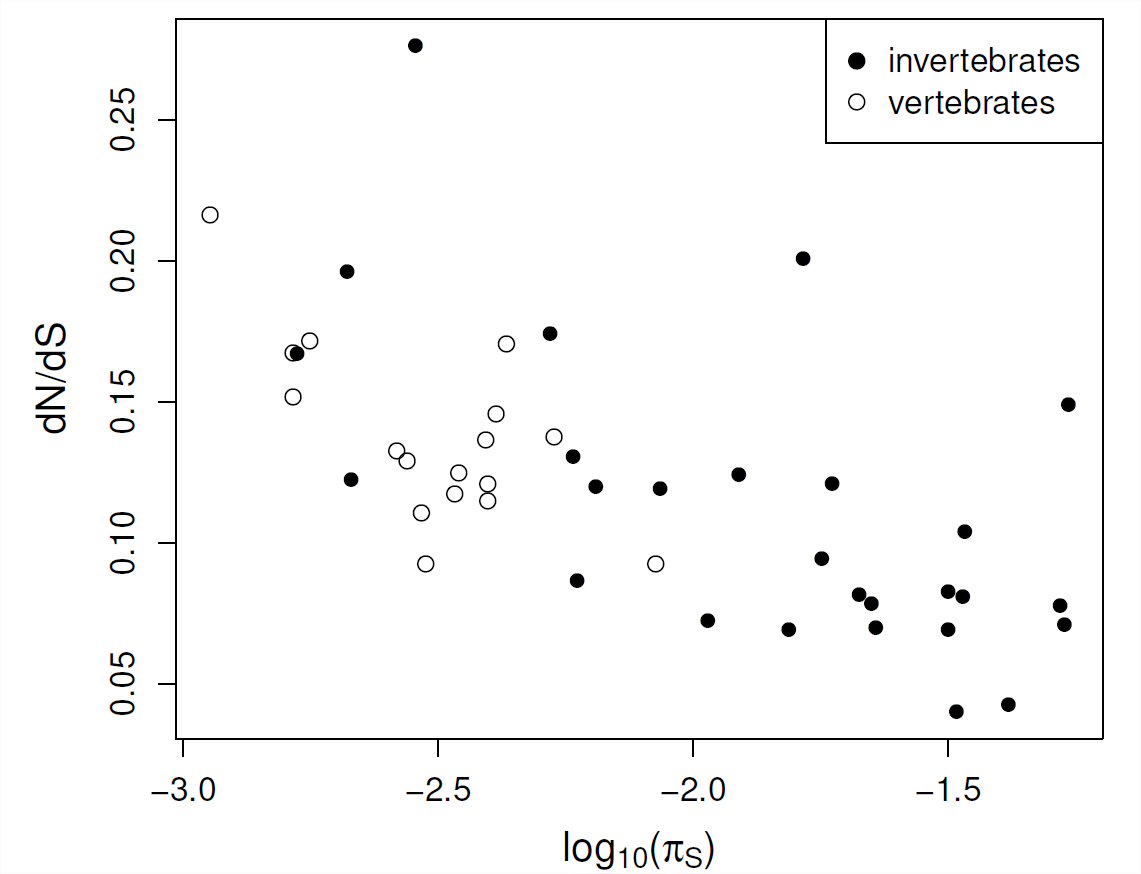
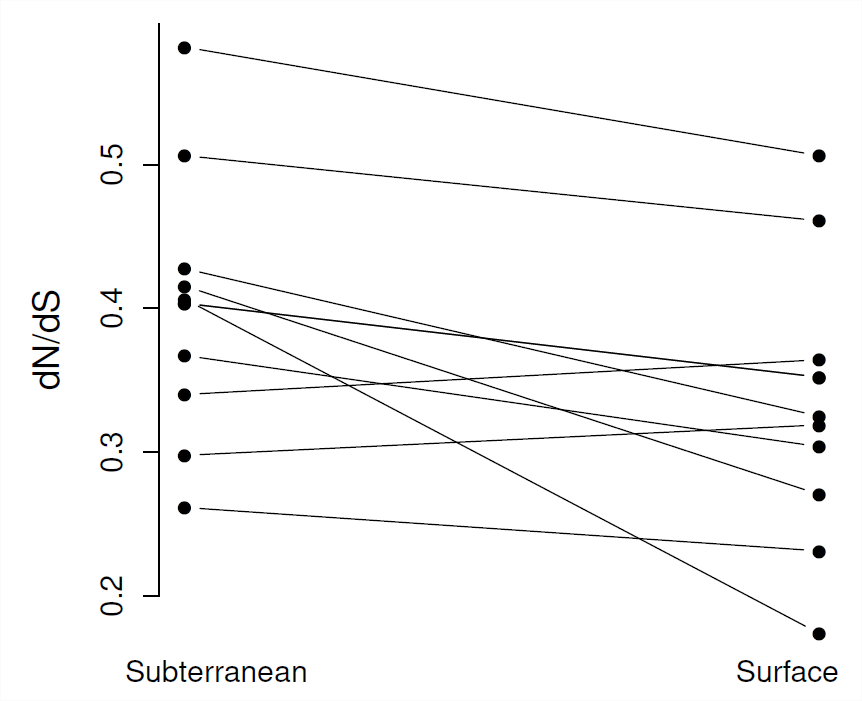
\(\frac{d_N}{d_S}\)У різних видах середні показники геному, здається, співвідносяться з показниками ефективної чисельності популяції (наприклад, синонімічного різноманіття), див\(\PageIndex{9}\). Рис. Ці дані підтверджують думку про те, що у видів з меншими ефективними розмірами популяції (меншими\(\pi_S\)) білки можуть піддаватися більш низьким ступеням обмеженості, оскільки дуже слабо згубні мутації здатні фіксувати. Таким чином, деяка розумна частка функціональних заміщень у популяціях з невеликими ефективними розмірами населення, таких як люди, може бути м'яко згубною.