4: Генетичний дрейф та нейтральне різноманіття
- Page ID
- 7736
Випадковість притаманна еволюції, від щасливих птахів здули курс на колонізацію якогось нового океанічного острова, до якого мутації виникають спочатку в штамі ВІЛ, що заражає індивіда, що приймає антиретровірусні препарати. Одним з основних джерел стохастичності в еволюційній біології є генетичний дрейф. Генетичний дрейф відбувається тому, що більш-менш копії алеля випадково можуть передаватися наступному поколінню. Це може статися тому, що випадково особини, що несуть певний алель, можуть залишити більш-менш потомство в наступному поколінні. У статевій популяції генетичний дрейф відбувається також тому, що передача Менделя означає, що потомству передається лише один з двох алелів у особини, обраний випадковим чином у місці.
Генетичний дрейф може відігравати певну роль у динаміці всіх алелів у всіх популяціях, але він відіграє найбільшу роль для нейтральних алелів. Нейтральний поліморфізм виникає, коли сегрегаційні алелі на поліморфному місці не мають помітних відмінностей у своєму впливі на фітнес. Пізніше ми пояснимо, що ми маємо на увазі під «помітним», але на даний момент вважаємо це «ніяким впливом» на фітнес.
Нейтральна теорія молекулярної еволюції
Роль генетичного дрейфу в молекулярній еволюції гаряче обговорюється з 60-х років, коли була запропонована Нейтральна теорія молекулярної еволюції. Центральна передумова нейтральної теорії полягає в тому, що закономірності молекулярного поліморфізму всередині видів і заміщення між видами можуть бути добре зрозумілі, припустивши, що переважна більшість цих молекулярних поліморфізмів і замін були нейтральними алелями, динаміка яких була просто підпорядкована капризам генетичний дрейф і мутація. Ранні прихильники цієї точки зору припустили, що переважна більшість нових мутацій є нейтральними або дуже шкідливими (наприклад, мутації, які порушують важливі функції білка). Цей останній клас мутацій занадто шкідливий, щоб сприяти загальним поліморфізмам або заміщенням між видами, оскільки вони швидко висіваються з популяції шляхом селекції.
Нейтральна теорія може здатися дивною, враховуючи, що більшу частину часу наша перша кисть з еволюцією часто фокусується на адаптації та фенотипічній еволюції. Однак прихильники цього світогляду не заперечували існування вигідних мутацій, вони просто думали, що корисні мутації досить рідкісні, що їх внесок в основну масу поліморфізму або розбіжності можна значною мірою ігнорувати. Вони також часто думали, що більша частина фенотипічної еволюції цілком може бути адаптивною, але знову ж таки локуси, відповідальні за ці фенотипи, є невеликою часткою всіх молекулярних змін, що відбуваються. Нейтральна теорія молекулярної еволюції спочатку була запропонована для пояснення поліморфізму білка. Однак ми можемо застосувати це ширше, щоб думати про нейтральну еволюцію в масштабі генома. З огляду на це, які типи молекулярних змін можуть бути нейтральними? Можливо:
- Зміни в некодуванні ДНК, які не порушують регуляторні послідовності. Наприклад, в геномі людини всього близько 2% кодів генома на білки. Решта здебільшого складається зі старих транспозіруваних елементів та ретровірусних вставок, повторів, псевдогенів та загального геномного безладу. Поточні оцінки свідчать про те, що навіть підраховуючи збережені, функціональні, некодуючі області, менше 10% нашого генома підлягають еволюційному обмеженню.
- Синонімічні зміни в областях кодування, тобто тих, які не змінюють амінокислоту, закодовану кодоном.
- Несинонімічні зміни, які не мають сильного впливу на функціональні властивості закодованої амінокислоти, наприклад зміни, які не змінюють розмір, заряд або гідрофобні властивості амінокислоти занадто сильно.
- Зміна амінокислоти з фенотипічними наслідками, але мало значення для фітнесу, наприклад, мутація, яка змушує ваші вуха бути дещо іншою формою, або яка заважає організму жити за 50 років у видах, де більшість особин розмножуються і вмирають до 20 років.
Існують зустрічні приклади для всіх цих ідей, наприклад, синонімічні зміни можуть вплинути на швидкість перекладу та точність білків і тому підлягають відбору. Однак, наведений вище список, сподіваємось, переконує вас, що загальне мислення про те, що якась частина молекулярних змін може не піддаватися відбору, не настільки глухе, як це, можливо, спочатку звучало.
Різні особливості молекулярного поліморфізму та дивергенції розглядаються як узгоджені з нейтральною теорією молекулярної еволюції. У цьому розділі ми зупинимося на прогнозуванні високого рівня молекулярного поліморфізму у багатьох видів (див. Наприклад, рис.\ ref {рис:Leffer}). У наступному розділі ми поговоримо про прогнозування молекулярного годинника. Ми побачимо, що різні аспекти оригінальної нейтральної теорії мають заслугу в описі деяких особливостей і типів молекулярних змін, але ми також побачимо, що це явно неправильно в деяких випадках. Ми також побачимо, що основна корисність нейтральної теорії полягає не в тому, чи є вона правильною чи неправильною, але в тому, що вона служить простою нульовою моделлю, яка може бути перевірена, а в деяких випадках відхилена, а згодом побудована. Більш широкою дискусією в галузі молекулярної еволюції є баланс нейтральних, адаптивних та згубних змін, які керують різними типами еволюційних змін.
Втрата гетерозиготності внаслідок дрейфу
Генетичний дрейф, за відсутності нових мутацій, повільно очищає наше населення від нейтрального генетичного різноманіття, оскільки алелі повільно дрейфують на високі або низькі частоти і з часом втрачаються або фіксуються.
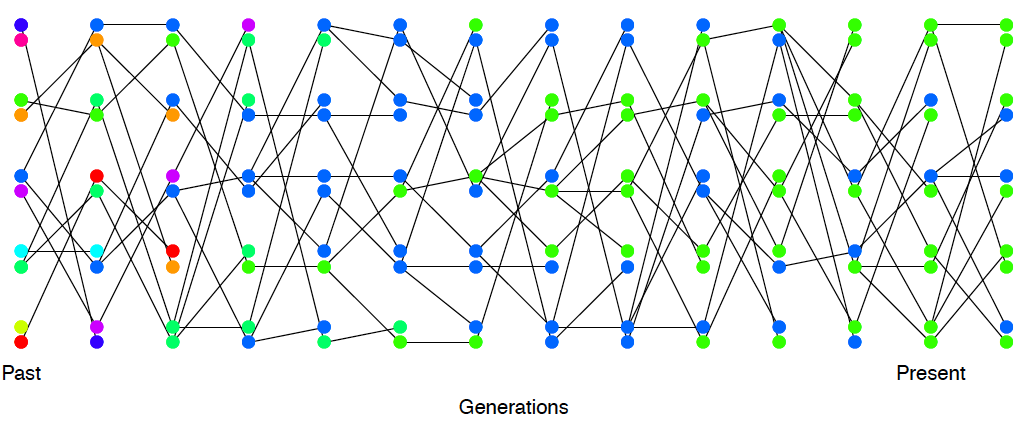
Уявіть собі випадкове спаровування популяції\(N\) диплоїдних особин постійного розміру, і що ми досліджуємо локус, що розділяє два алелі, нейтральні по відношенню один до одного. Ця популяція випадковим чином спаровується по відношенню до алелей в цьому місці. Див. Рисунок Рисунок\(\PageIndex{1}\) і малюнок,\(\PageIndex{2}\) щоб побачити, як протікає генетичний дрейф, відстежуючи алелі в межах невеликої популяції
У генерації\(t\) наш нинішній рівень гетерозиготності є\(H_t\), тобто ймовірність того, що два випадково вибіркових алелі в генерації\(t\) неідентичні є\(H_t\). Якщо припустити, що швидкість мутації дорівнює нулю (або зникающе мала), який у нас рівень гетерозиготності в генерації\(t+1\)?
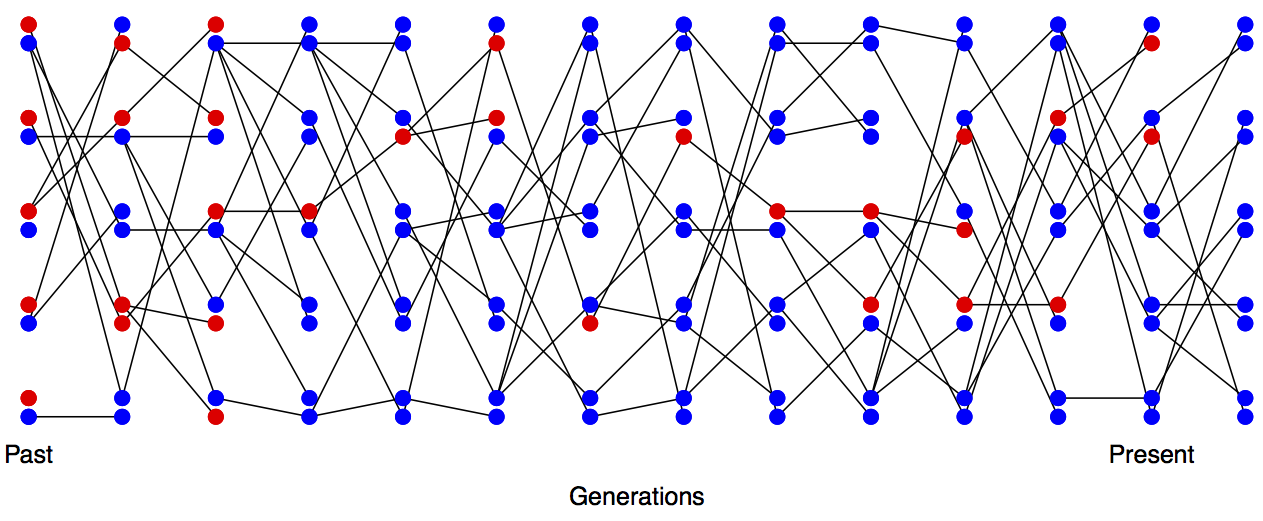
У наступному поколінні (\(t+1\)) ми дивимося на алелі в потомстві покоління\(t\). Якщо ми випадковим чином відбираємо два алелі в генерації,\(t+1\) які мали різні батьківські алелі в поколінні\(t\), це так само, як малювання двох випадкових алелів з покоління\(t\). Таким чином, ймовірність того, що ці два алелі в генерації\(t+1\), які мають різні батьківські алелі в генерації\(t\), є неоднаковими є\(H_t\).
І навпаки, якщо два алелі в нашій парі мали однаковий батьківський алель у поточному поколінні (тобто алелі ідентичні по спуску на одне покоління назад), то ці два алелі повинні бути однаковими (оскільки ми не допускаємо жодної мутації).
У диплоїдної популяції великих\(N\) особин є\(2N\) алелі. Імовірність того, що наші два алелі мають однаковий батьківський алель у поточному поколінні, є\(\frac{1}{(2N)}\) і ймовірність того, що вони мають різні батьківські алелі, є\(1-\frac{1}{(2N)}\). Отже, за вищевказаним аргументом очікувана гетерозиготність в генерації\(t+1\) становить
\[H_{t+1} = \frac{1}{2N} \times 0 + \left(1-\frac{1}{2N} \right)H_t\]
Таким чином, якщо гетерозиготність в генерації\(0\) є\(H_0\), то наша очікувана гетерозиготність в генерації\(t\) становить
\[H_t = \left(1-\frac{1}{2N} \right)^tH_0 \label{eqn:loss_het_discrete}\]
тобто очікувана гетерозиготність всередині нашої популяції геометрично розпадається з кожним поколінням. Якщо ми припустимо, що\(\frac{1}{(2N)} \ll 1\) тоді ми можемо наблизити цей геометричний розпад експоненціальним розпадом (див. Питання\ ref {geoquestion} нижче), такий, що
\[H_t =H_{0} e^{ - \frac{t}{(2N)} }\]
тобто гетерозиготність розпадається експоненціально зі швидкістю\(\frac{1}{(2N)}\).
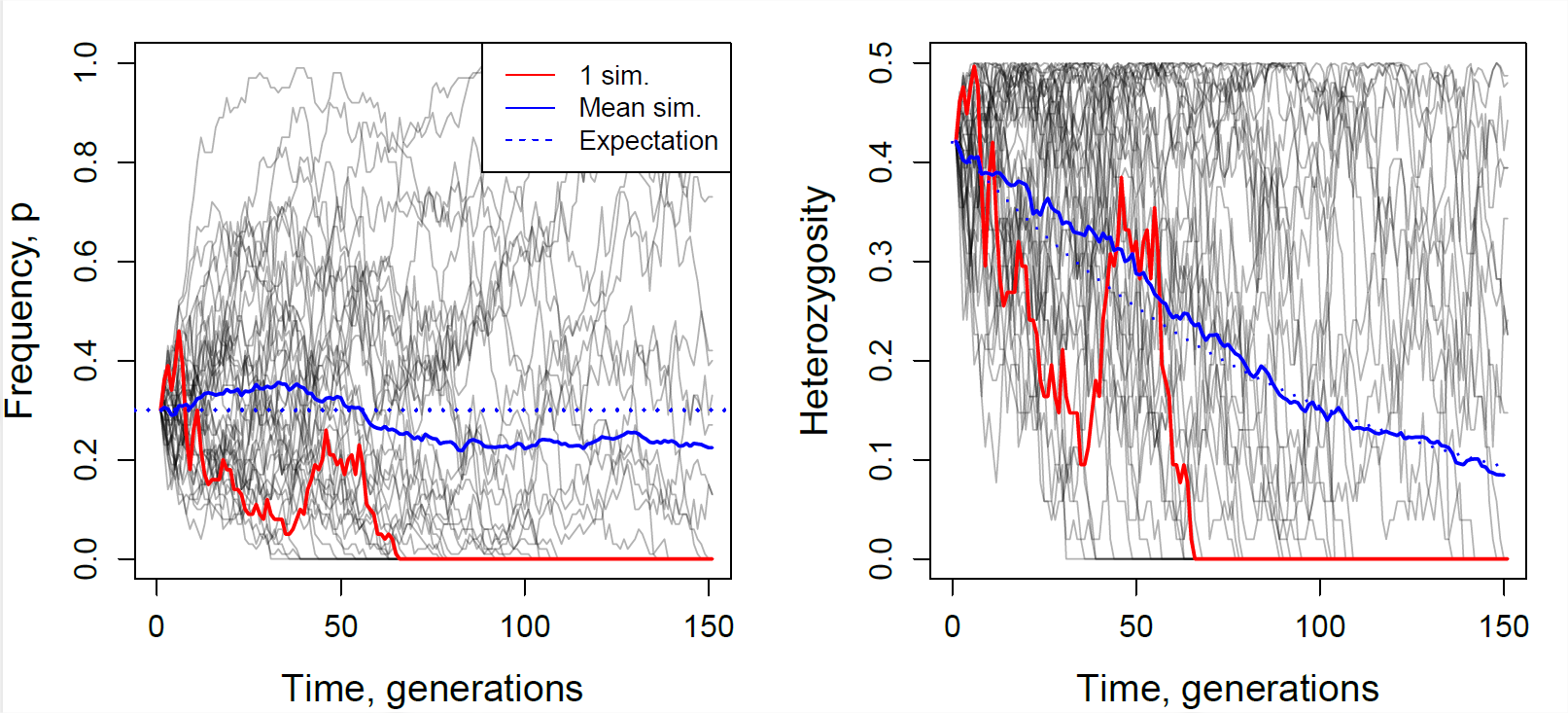
На малюнку\ ref {Fig:losShet_WF_n50} ми показуємо траєкторії через час для 40 незалежно змодельованих локусів, дрейфуючих в популяції 50 особин. Кожне населення було започатковано з частоти\(30\%\). Деякі дрейфують вгору, а деякі дрейфують вниз, врешті-решт втрачаються або фіксуються від населення, але, в середньому по моделюванню, частота алелів не змінюється. Ми також відстежуємо гетерозиготність, ви можете бачити, що гетерозиготність іноді зростає, а іноді знижується, але в середньому ми втрачаємо гетерозиготність, і ця швидкість втрат добре прогнозується Equation\ ref {eqn:loss_het_discrete}.
Ви відповідаєте за підтримку населення дельти корюшки в дельті річки Сакраменто. Використовуючи великий набір мікросупутників, ви оцінюєте, що середній рівень гетерозиготності в цій популяції становить 0,005. Ви ставите собі за мету зберегти рівень гетерозиготності не менше 0,0049 протягом наступних двохсот років. Припускаючи, що корюшка має час покоління в 3 роки, і що тільки генетичний дрейф впливає на ці локуси, яка найменша повністю аутбридирующая популяція, яку вам потрібно було б підтримувати для досягнення цієї мети?
Зверніть увагу, як ця картина зменшення гетерозиготності стоїть на відміну від узгодженості рівноваги Харді-Вайнберга з попередньої глави. Однак наші пропорції Харді-Вайнберга все ще тримаються у формуванні кожного нового покоління. Оскільки генотипи потомства в наступному поколінні (\(t+1\)) представляють собою випадкову нічию з попереднього покоління (\(t\)), якщо батьківська частота є\(p_t\), ми очікуємо, що частка\(2p_t(1-p_t)\) нашого потомства буде гетерозиготами (і HW пропорції для наших гомозигот). Однак, оскільки чисельність популяції кінцева, спостережувані частоти генотипу у потомства (ймовірно) не будуть точно відповідати нашим очікуванням. Оскільки наші частоти генотипу, ймовірно, дещо змінюються через вибірку, біологічно це відображає випадкові зміни розміру сім'ї та менделівської сегрегації, частота алелів зміниться. Тому, хоча кожне покоління представляє зразок з пропорцій Харді-Вайнберга на основі покоління раніше, наші пропорції генотипу не знаходяться в рівновазі (незмінному стані), оскільки основна частота алелів змінюється протягом поколінь. Пізніше ми розробимо деякі математичні моделі для цих змін частоти алелів. Поки що просто відзначимо, що під нашою простою моделлю дрейфу (формально модель Райта-Фішера) наша кількість алелів у\(t+1^{th}\) генерації являє собою біноміальну вибірку (розміру\(2N\)) від частоти популяції\(p_t\) в попередньому поколінні. Якщо ви читали тут, будь ласка, напишіть Проф Куп фотографію JBS Haldane в смугастому костюмі з назвою «Я читаю главу 3 примітки». (Варто погуглити JBS Haldane і прочитати більше про його життя; він справжній персонаж і один з останніх великих поліматів.)
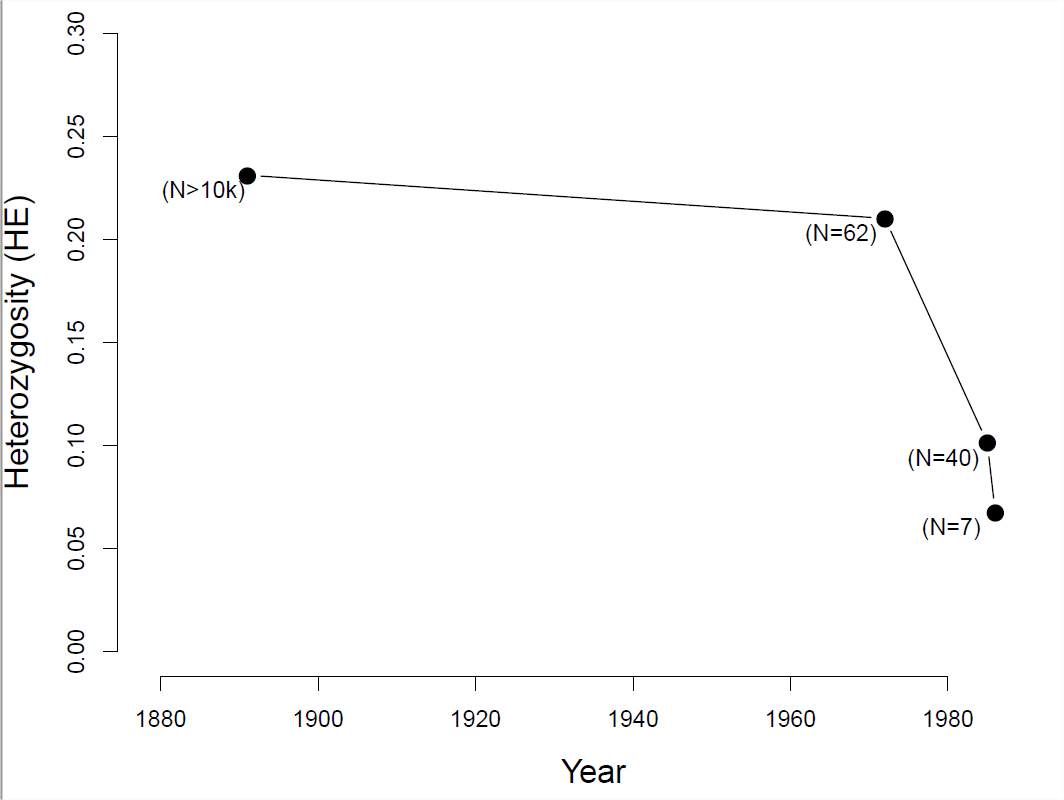
Щоб побачити, як зменшення чисельності популяції може вплинути на рівень гетерозиготності, розглянемо випадок чорноногих тхорів (Mustela nigripes). Популяція чорноногих тхорів різко скоротилася протягом ХХ століття через руйнування місця їх проживання та сильватичної чуми. У 1979 році, коли останній відомий чорноногий тхір помер в неволі, їх вважали вимерлими. У 1981 році була заново відкрита дуже невелика дика популяція (\(40\)особини), але в 1985 році ця популяція перенесла ряд спалахів захворювань.
У цей момент\(18\) залишилися дикі особини були виведені в полон, 7 з яких відтворювали. Завдяки інтенсивним зусиллям з розведення неволі та збереженню дикої популяції з тих пір було створено понад 300 особин. Однак, оскільки всі ці особи походять від тих 7 осіб, які пережили вузьке місце, рівні різноманітності залишаються низькими. виміряна гетерозиготність в ряді мікросупутників у осіб з музейних колекцій, показуючи різке падіння різноманітності у міру краху чисельності населення (див. Рис. {Рис: втратити тхори}).
У математичній популяційній генетиці зазвичай використовується наближення\((1-x) \approx e^{-x}\) для\(x << 1\) (формально це випливає з розширення серії Тейлора\(\exp(-x)\), ігноруючи другого порядку та вищі члени\(x\), див. Додаток\ ref {EQN:Taylor_Geo}). Це наближення особливо корисно для наближення процесу геометричного розпаду експоненціальним процесом розпаду, наприклад\((1 - x)^t \approx e^{-xt}\). За допомогою калькулятора або R перевірте, наскільки добре цей вираз наближає точний вираз для двох значень\(x\)\(x = 0.1\), і\(0.01\), для двох різних значень t,\(t=5\) і\(t=50\). Коротко прокоментуйте свої результати.
Рівні різноманітності підтримуються балансом між мутацією і дрейфом
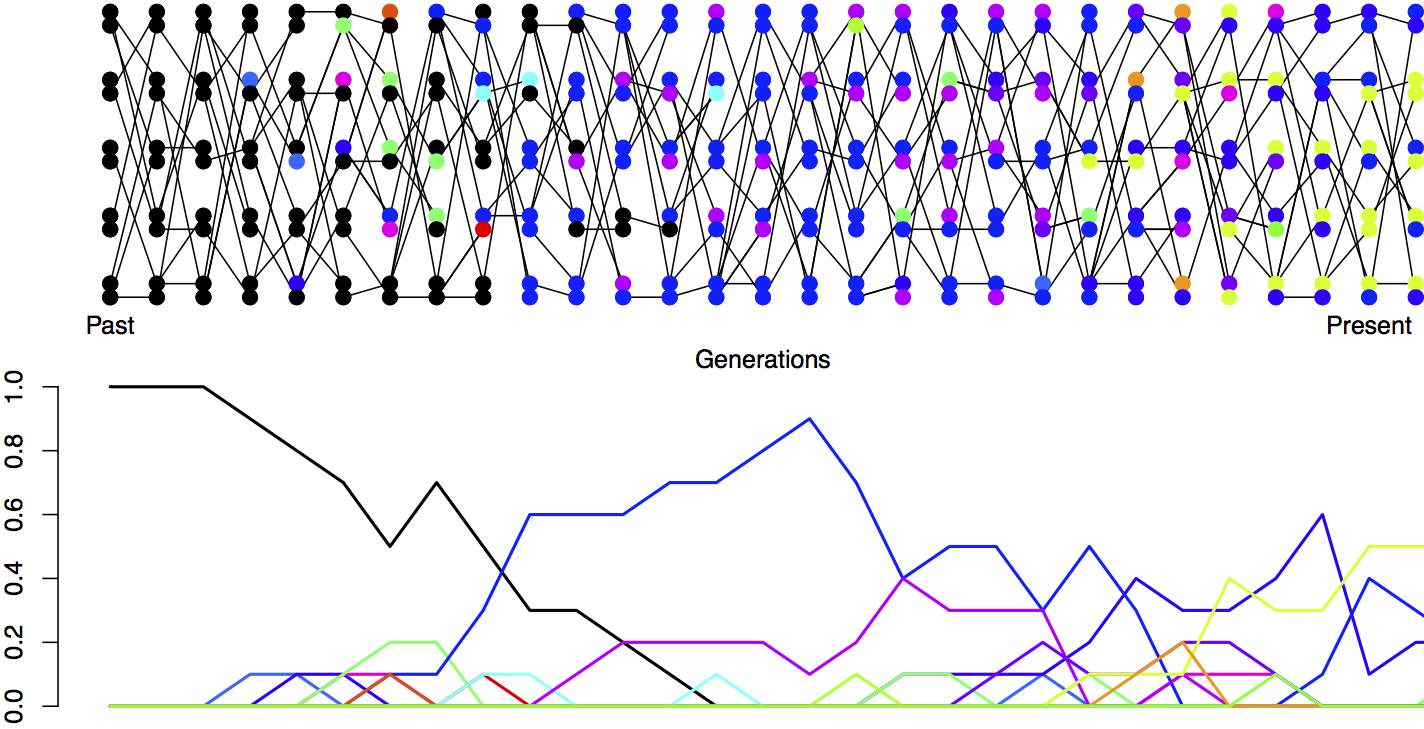
Далі ми розглянемо кількість нейтрального поліморфізму, який може підтримуватися в популяції, як баланс між варіацією видалення генетичного дрейфу та мутацією, що вводить нову нейтральну варіацію, див. Рисунок\ ref {fig:mut_sel_balance} для прикладу. Відзначимо в нашому прикладі, як жоден алель не підтримується при стабільній рівновазі, скоріше рівноважний рівень поліморфізму підтримується постійно зсувається набором алелів.
Нейтральна швидкість мутації
Спочатку ми хочемо розглянути швидкість, з якою виникають нейтральні мутації в популяції.Повертаючись до нашого обговорення нейтральної теорії молекулярної еволюції, припустимо, що існує лише два класи мутацій, які можуть виникнути в нашій геномній області, що представляє інтерес: нейтральні мутації та високо згубні мутації. Загальна швидкість мутації в нашому локусі -\(\mu\) на покоління, тобто за передачу від батьків до дитини. \(C\)Частка наших мутацій - це нові алелі, які дуже шкідливі і так швидко видаляються з популяції. Ми назвемо цей\(C\) параметр обмеженням, і він буде відрізнятися залежно від розглянутої нами геномної області. Частка, що залишилася\((1-C)\) - це наші нейтральні мутації, такі, що наша нейтральна швидкість мутації\((1-C)\mu\). Це показник за генерацію. В іншій частині глави для простоти ми будемо вважати, що\(C=0\) і використовувати нейтральну швидкість мутації\(\mu\). Однак ми повернемося до цього обговорення обмеження, коли ми обговоримо молекулярну дивергенцію в наступному розділі.
Варто витратити хвилинку, щоб ознайомитися як з тим, наскільки рідкісна, так і поширена мутація. Швидкість мутації на базову пару у людей становить приблизно\(1.5\)\(\times\)\(10^{-8}\) на покоління. Це означає, що в середньому ми повинні контролювати сайт для\(\sim 66.6\) мільйонів передач від батьків до дитини, щоб побачити мутацію. Проте популяції та геноми є великими місцями, тому мутації поширені на цих рівнях.
- Ваш аутосомний геном становить\(\sim\) 3 мільярди пар основ long (\(3\)\(\times\)\(10^9\)). У вас є дві копії, той, який ви отримали від своєї мами, і один від тата. Яка середня (тобто очікувана) кількість мутацій, що сталися при передачі від вашої мами і тата до вас?
- Нинішня чисельність людської популяції становить\(\sim\) 7 мільярдів особин. Скільки разів, на рівні всього людського населення, мутувала одна база-пара при передачі від одного покоління до наступного?
Рівні гетерозиготності підтримуються як баланс між мутацією і дрейфом
Озираючись назад у часі від одного покоління до попереднього покоління, ми скажемо, що два алелі, які мають однаковий батьківський алель (тобто знаходять свого спільного предка) у попередньому поколінні, об'єдналися і називають цю подію як коалесцируючою подією. Якщо наші пари алелів повинні відрізнятися один від одного в наші дні, мутація повинна відбутися зовсім недавно на тій чи іншій лінії, перш ніж вони знайшли спільного предка.
Імовірність того, що наша пара випадково відібраних алелів об'єдналися в попередньому поколінні\(\frac{1}{(2N)}\), є, і ймовірність того, що наша пара алелів не змогла згуртуватися, є\(1-\frac{1}{(2N)}\).
Імовірність того, що мутація змінює ідентичність переданого алеля, є\(\mu\) на покоління. Таким чином, ймовірність того, що мутація не відбувається, є\((1-\mu)\). Ми припустимо, що коли відбувається мутація, вона створює якийсь новий алельний тип, якого немає в популяції. Це припущення (яке зазвичай називають моделлю нескінченно-багато-алелей) робить математику трохи чистішою, а також не надто поганим припущенням біологічно. Див. Рисунок\ ref {fig:mut_SEL_balance} для опису балансу мутації-дрейфу в цій моделі протягом поколінь.
Ця модель дозволяє нам обчислити, коли наші два алелі востаннє поділилися спільним предком і чи однакові ці алелі внаслідок неможливості мутувати, оскільки цей спільний предок. Наприклад, ми можемо визначити ймовірність того, що наші два випадково відібрані алелі зливаються\(2\) поколіннями в минулому (тобто вони не об'єднуються в генерації,\(1\) а потім зливаються в генерації\(2\)), і що вони ідентичні, як
\[\left(1- \frac{1}{2N} \right) \frac{1}{2N} (1-\mu)^4\]
Зверніть увагу, що сила\(4\) полягає в тому, що наші два алелі повинні були не мутувати через\(2\) мейози кожен.
Більш загально, ймовірність того, що наші алелі зливаються в генерації\(t+1\) (підраховуючи назад у часі) і ідентичні через відсутність мутації ні до одного з алелів у наступних поколіннях, становить
\[\mathbb{P}(\textrm{coal. in t+1 \& no mutations}) = \frac{1}{2N} \left(1- \frac{1}{2N} \right)^t \left(1-\mu \right)^{2(t+1)}\]
Щоб зробити це трохи простіше для себе, давайте далі припустимо, що\(t \approx t+1\) і так перепишіть це як:
\[\mathbb{P}(\textrm{coal. in t+1 \& no mutations}) \approx \frac{1}{2N} \left(1- \frac{1}{2N} \right)^t \left(1-\mu \right)^{2t}\]
Це дає нам приблизну ймовірність того, що два алелі зростуться в\((t+1)^\text{th}\) генерації. Загалом, ми можемо не знати, коли два алелі можуть злитися: вони можуть злитися в\(t=1, t=2, \ldots\) поколінні тощо. Таким чином, щоб обчислити ймовірність того, що два алелі зливаються в будь-якому поколінні перед мутацією, ми можемо написати:
\[\begin{aligned} \mathbb{P}(\textrm{coal. in any generation \& no mutations}) \approx & \mathbb{P}(\textrm{coal. in} \; t=1 \; \textrm{\& no mutations}) \; + \nonumber\\ & \mathbb{P}(\textrm{coal. in} \; t=2 \; \textrm{\& no mutations}) + \ldots \nonumber\\ %P(\textrm{coal. in} \; t=3 \; \textrm{\& no mutations}) +\ldots \nonumber\\ = & \sum_{t=1}^\infty \mathbb{P}(\textrm{coal. in } \; t \; \textrm{generations \& no mutation})\end{aligned}\]
Приклад використання Закону повної ймовірності див. Додаток Equation\ ref {eqn:law_tot_prob}, поєднане з тим, що коалесцирование в конкретному поколінні є взаємовиключним з коалесцируванням в іншому поколінні.
Хоча ми могли б обчислити значення для цієї суми\(\mu\), заданої\(N\) і, важко отримати уявлення про те, що відбувається з таким складним виразом. Тут ми переходимо до загального наближення в популяційній генетиці (і всієї прикладної математики), де ми припускаємо, що\(\frac{1}{(2N)} \ll 1\) і\(\mu \ll 1\). Це дозволяє нам наблизити геометричний розпад як експоненціальний розпад (див. Додаток Рівняння\ ref {Eqn:Taylor_exp}). Тоді ймовірність того, що два алелі зливаються в генерації\(t+1\) і не мутують, можна записати як:
\[\begin{aligned} \mathbb{P}(\textrm{coal. in t+1 \& no mutations}) &\approx \frac{1}{2N} \left(1- \frac{1}{2N} \right)^t \left(1-\mu \right)^{2t} \\ & \approx \frac{1}{2N} e^{-t/(2N)} e^{-2\mu t } \\ &=\frac{1}{2N} e^{-t(2\mu+1/(2N))} \end{aligned}\]
Тоді ми можемо наблизити підсумовування інтегралом, давши нам:
\[\frac{1}{2N} \int_0^{\infty} e^{-t(2\mu+1/(2N))} dt = \frac{1/(2N)}{1/(2N)+2\mu} \label{eqn:coal_no_mut}\]
Наведене вище рівняння дає нам ймовірність того, що наші два алелі зливаються в якийсь момент часу і не мутують, перш ніж досягти свого спільного предка. Аналогічно, це можна розглядати як ймовірність того, що наші два алелі зливаються перед мутуванням, тобто, що вони гомозиготні.
Тоді, додаткова ймовірність того, що наша пара алелей неідентична (або гетерозиготна) - це просто один мінус цього. Наступне рівняння дає рівноважну гетерозиготність в популяції при рівновазі між мутацією і дрейфом:
\[H = \frac{2\mu}{1/(2N)+2\mu} = \frac{4N\mu}{1+4N\mu} \label{eqn:hetero}\]
\(4N\mu\)З'єднаний параметр, масштабований масштабуванням населення швидкість мутації, з'явиться кілька разів, тому ми дамо йому власне ім'я:
\[\theta = 4N\mu\]
Яка інтуїція нашого\ ref {eqn:hetero}, ну ймовірність того, що будь-яка подія трапиться в певному поколінні є\(\mathbb{P}(\textrm{mutation or coalescence}) \approx \frac{1}{(2N)}+2\mu\), так умовно від події відбувається ймовірність того, що це мутація є\(\mathbb{P}(\textrm{mutation} \mid \textrm{mutation or coalescence}) = \frac{2\mu}{\left(\frac{1}{(2N)}+2\mu \right)}\).
Тож за інших рівних умов види з більшими розмірами населення повинні мати пропорційно вищий рівень нейтрального поліморфізму. Дійсно, популяції тварин, наприклад, птахів, на невеликих островах мають менший рівень різноманітності, ніж близькоспоріднених видів на материку з більшими ареалами. У загальному плані ми бачимо більш високі рівні гетерозиготності в більших розмірах перепису населення між тваринами Рисунок\ ref {рис:Allozyme_n}. Однак, хоча чисельність населення перепису коливається на багато порядків, рівні різноманітності різняться набагато менше, ніж це. Отже, якщо рівні різноманітності в природних популяціях являють собою баланс між генетичним дрейфом та мутацією, рівні генетичного дрейфу у великих популяціях повинні бути набагато швидшими, ніж передбачає їх чисельність перепису населення. У наступному розділі ми поговоримо про деякі можливі причини, чому.

Ефективна чисельність населення
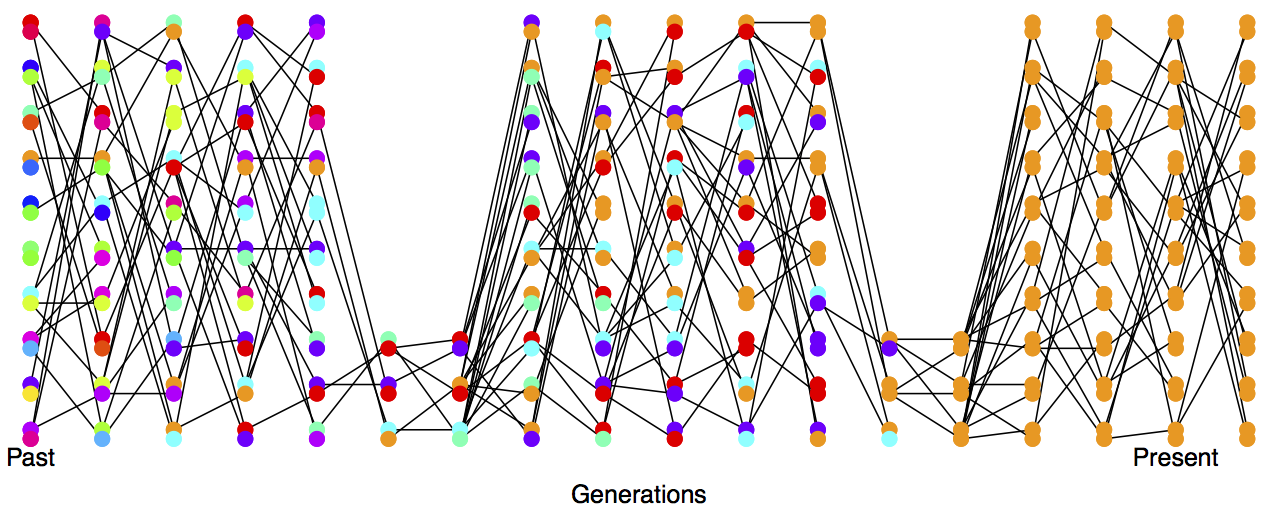
На практиці популяції рідко відповідають нашим припущенням бути постійними в розмірах з низькою дисперсією в репродуктивному успіху. Реальні популяції відчувають різкі коливання розмірів, і часто спостерігається велика дисперсія в репродуктивному успіху. Таким чином, темпи дрейфу природних популяцій часто набагато вищі, ніж передбачається чисельність населення перепису населення. Див. Рисунок\ ref {Fig:losshet_varying_pop} для зображення багаторазово вузьких місць населення, яке швидко втрачає різноманітність.
Щоб впоратися з цією невідповідністю, популяційні генетики часто посилаються на концепцію ефективної чисельності популяції (\(N_e\)). У багатьох ситуаціях (але не у всіх) відступи від модельних припущень можуть бути зафіксовані шляхом\(N_e\) заміни\(N\).
Якщо чисельність населення швидко змінюється за розміром, ми можемо (при дотриманні певних умов) замінити чисельність нашої популяції гармонійною середньою чисельністю населення. Розглянемо диплоїдну популяцію змінного розміру, розмір якої становить\(N_t\)\(t\) покоління в минуле. Імовірність того, що наші пари алелів не зрослися за поколінням\(t\), задається
\[\prod_{i=1}^{t} \left(1-\frac{1}{2N_i} \right) \label{eqn:var_pop_coal}\]
Зауважте, що це просто згортається до нашого вихідного виразу\(N_i\),\(\left(1-\frac{1}{2N } \right)^t\) якщо є постійним. За цією моделлю швидкість втрати гетерозиготності у цієї популяції еквівалентна популяції ефективного розміру
\[N_e =\frac{1}{\frac{1}{t} \sum_{i=1}^{t} \frac{1}{N_i} }. \label{eq:Ne_harmonic}\]
Це гармонійне середнє значення різної чисельності населення.
Таким чином, наш ефективний розмір популяції, розмір ідеалізованої постійної популяції, яка відповідає швидкості генетичного дрейфу, є гармонійним середнім істинним розміром популяції з часом. На гармонійне середнє дуже сильно впливають невеликі значення, такі, що якщо чисельність нашого населення становить один мільйон\(99\%\) часу, але падає до\(1000\) кожної сотні або близько того поколінь,\(N_e\) буде набагато ближче до\(1000\) мільйона.
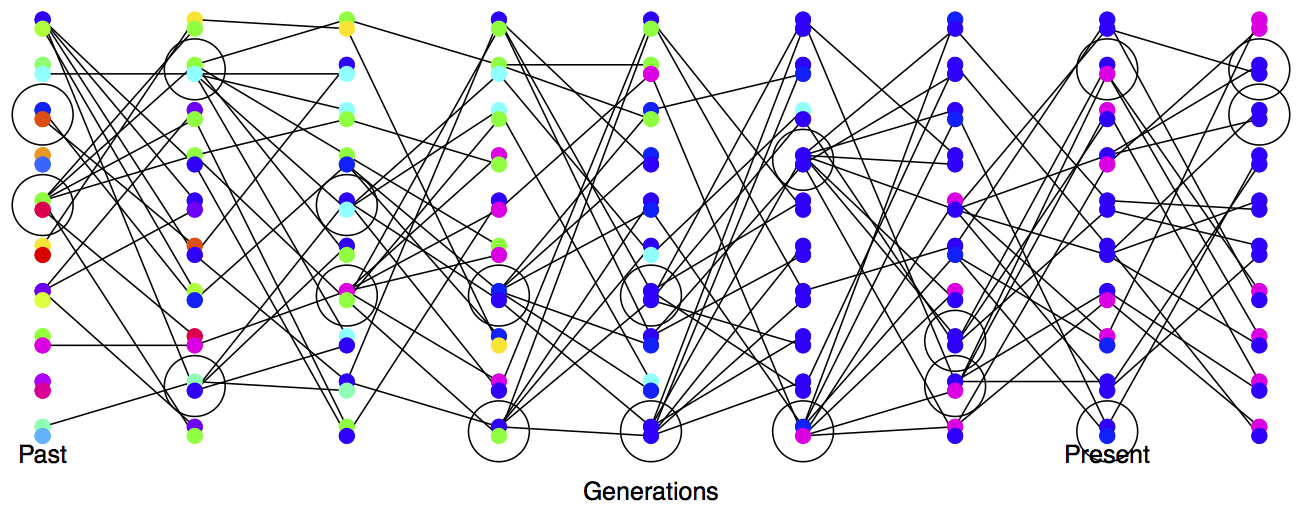
Дисперсія в репродуктивному успіху також вплине на нашу ефективну чисельність населення. Навіть якщо наша популяція має велику постійну величину\(N\) особин, якщо тільки мала частка з них добирається до розмноження, то швидкість дрейфу буде відображати це набагато менша кількість відтворюються особин. Див. Рисунок\ ref {fig:losshet_varying_rs} для зображення більш високої швидкості дрейфу в популяції, де є висока дисперсія в репродуктивному успіху.
Щоб побачити один із прикладів цього, розглянемо випадок, коли\(N_F\) самки отримують розмноження, а\(N_M\) самці отримують розмноження. Хоча кожна людина має біологічну матір і батько, не кожна людина стає батьком. На практиці у багатьох видів тварин розмножуються набагато більше самок, ніж самці, тобто\(N_M <N_F\), оскільки кілька самців отримують багато можливостей для спарювання, а багато самців не отримують жодної або мало можливостей для спарювання. Коли наші два алелі вибирають предка,\(25\%\) того часу наші алелі були обидва у предка жінки, і в цьому випадку вони є IBD з ймовірністю\(1/(2N_F)\), і\(25\%\) того часу вони обидва знаходяться у предка чоловічої статі, і в цьому випадку вони зливаються з ймовірністю \(1/(2N_M)\). \(50\%\)Решту часу наші алелі простежуються до двох особин різної статі в попередньому поколінні і тому не можуть злитися. Тому наша ймовірність коалесценції в попередньому поколінні становить
\[\frac{1}{4}\left(\frac{1}{2N_M} \right)+\frac{1}{4}\left(\frac{1}{2N_F} \right) %= %\frac{1}{8}\frac{N_F+N_M}{N_FN_M}\]
тобто швидкість коалесценції є гармонійним середнім чисельністю популяції двох статей, прирівнюючи це до того, що\(\frac{1}{2N_e}\) ми знаходимо
[Рис: Гамадриа_бабуїн]
\[N_e = \frac{4N_FN_M}{N_F+N_M}\]
Таким чином, якщо репродуктивний успіх дуже перекошений в одній статі (наприклад\(N_M \ll N/2\)), наш аутосомно-ефективний розмір популяції в результаті значно зменшиться. Детальніше про те, як різні еволюційні сили впливають на швидкість генетичного дрейфу, і їх вплив на ефективну чисельність популяції дивіться в статті.
Ви вивчаєте населення з 500 чоловічих і 500 жіночих бабуїнів Гамадрій. Припустимо, що всі самки, але тільки 1/10 самців отримують спаровування. Який ефективний розмір популяції для аутосоми?
Дисперсія в репродуктивному успіху чоловіків і жінок може мати дуже різний вплив на хромосоми з різними режимами успадкування, такими як Х-хромосома, мітохондрії та Y-хромосома. Мітохондрії (мтДНК) та Y-хромосома є гаплоїдними і успадковуються лише через жінок та чоловіків відповідно, тому вони мають гаплоїдні ефективні розміри населення\(N_M\) і\(N_F\).

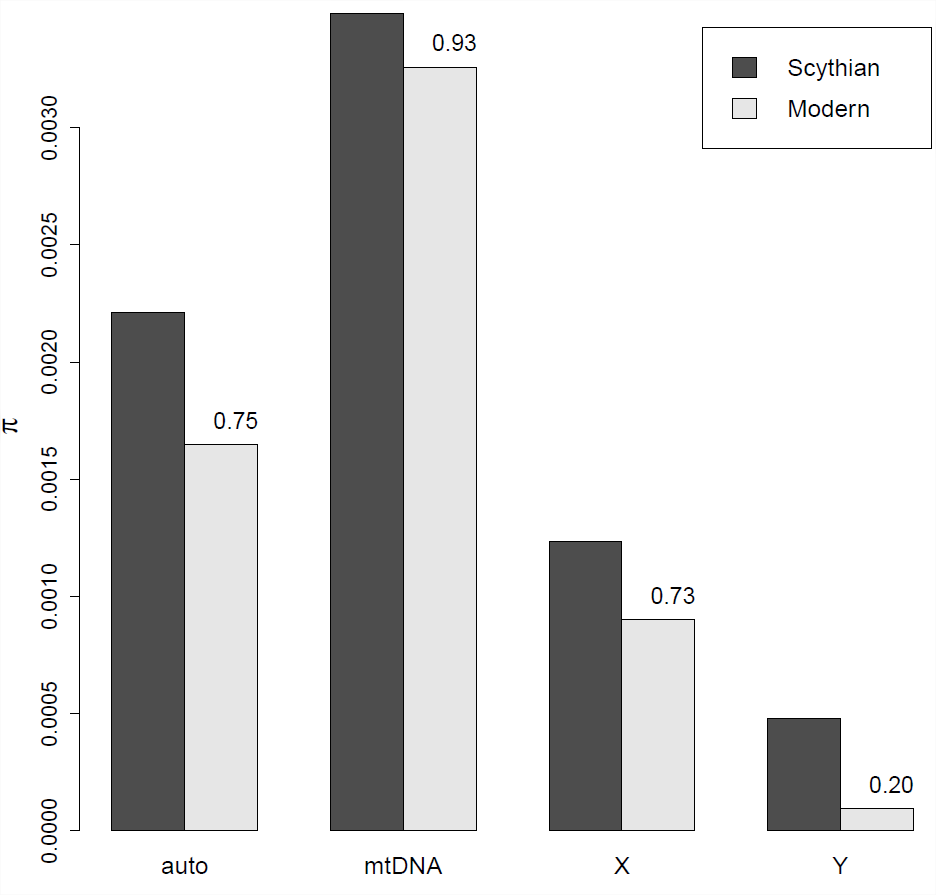 Рівні геномного різноманіття у скіфських коней від\(2300\) однорічних скіфських коней та сучасних коней (нордичних). Числа поруч з кожним стовпцем дають частку різноманітності, що залишилася на сьогоднішній день, Дані з.
Рівні геномного різноманіття у скіфських коней від\(2300\) однорічних скіфських коней та сучасних коней (нордичних). Числа поруч з кожним стовпцем дають частку різноманітності, що залишилася на сьогоднішній день, Дані з.Щоб побачити вплив диференціальної дисперсії на репродуктивний успіх чоловіків і жінок, давайте розглянемо, як рівень генетичного різноманіття протягом тисяч років у домашніх коней.

секвенована давня ДНК з 13 принесених в жертву жеребців з\(2300\) однорічного скіфського кургану в Казахстані. Скіфи були кочовим народом, чия російська степова імперія простягалася від Чорного моря до кордонів Китаю. Вони були одними з перших людей, які освоїли кінну війну як з чоловіками, так і жінками, які їхали, озброєні короткими луками.
Порівнюючи ці дані з сучасними кіньми, виявили, що рівні різноманітності були значно знижені на аутосомах і значно знижені на Y-хромосомі. Це контрастує з мтДНК, де рівні різноманітності знизилися лише незначно. Ця закономірність, ймовірно, відображає той факт, що більша частина сучасного конярства покладається на розведення невеликої кількості жеребців до великої кількості кобил, і тому ефективний розмір популяції Y-хромосоми був набагато меншим, ніж мтДНК, що призводить до набагато вищої швидкості втрати різноманітності на Y, ніж на інші хромосоми.
Використовуючи дані про зменшення генетичного різноманіття коней на малюнку\ ref {fig:Scythian_horses_PI}:
- Оцініть ефективну кількість жеребців та кобил, що сприяють популяції коней, використовуючи дані мтДНК та Y-хромосоми
- Передбачити, яке зменшення різноманітності протягом\(2300\) багатьох років має бути на аутосомах, використовуючи ці цифри?
Припустимо час покоління коней\(8\) років. Припустимо, що за цей проміжок часу немає нових мутацій.
Один з найвищих рівнів генетичного різноманіття спостерігається в диплоїдний розщеплено-зябровий гриб, Schizophyllum commune. Популяції в США мають гетерозиготність на рівні послідовності\(0.13\) на синонімічну базу. секвеновані батьки та кілька потомств, щоб оцінити це\(\mu= 2 \times 10^{-8} bp^{-1}\) на покоління. Яка ваша оцінка ефективної чисельності населення с . комуни?
_(33389628036).jpg)
Коалесцированіе і закономірності нейтрального розмаїття
«Життя можна зрозуміти лише назад; але воно повинно бути прожито вперед» - Kierkegaard
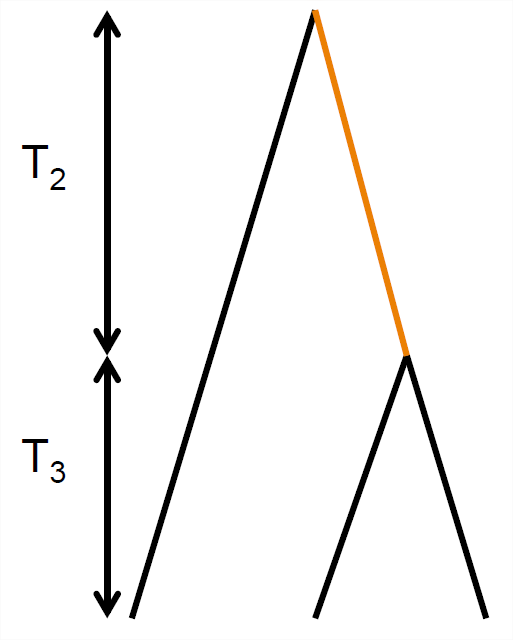
Попарний розподіл часу коалесценції та кількість попарних відмінностей.
Повернувшись до наших розрахунків, які ми зробили про втрату нейтральної гетерозиготності та рівноважних рівнів різноманітності (у розділах 1.1 та 1.1.1), ви зауважте, що ми могли б спочатку вказати, в якій генерації пара послідовностей зливається, а потім обчислити деякі властивості гетерозиготність виходячи з цього. Це тому, що нейтральні мутації не впливають на ймовірність того, що людина передає алель, і тому не впливають на те, як ми можемо простежити родові лінії через покоління.
Таким чином, часто буде корисно розглянути час до спільного предка пари послідовностей (\(T_2\)), а потім подумати про вплив того часу на злиття на закономірності різноманітності. Див. Рисунок\ ref {Fig:Coalescent_simulation} для прикладу цього.

Імовірність того, що пара алелів не змогла зібратися в\(t\) поколіннях, а потім зростися в\(t+1\) поколінні назад, становить
\[\mathbb{P}(T_2=t+1) = \frac{1}{2N} \left(1- \frac{1}{2N} \right)^{t} \label{eqn:coal_time_dist}\]
Наприклад, ймовірність того, що пара послідовностей зливається три покоління назад, - це ймовірність того, що вони не згуртуються в поколіннях 1 і 2\(\left(1- \frac{1}{2N} \right) \times \left(1- \frac{1}{2N} \right)\), що множиться на ймовірність того, що вони знаходять спільного предка, тобто злиття, в третьому поколінні, що відбувається з ймовірність\(\frac{1}{2N}\).
З форми Equation\ ref {eqn:coal_time_dist} ми бачимо, що час коалесценції нашої пари алелей є геометрично розподіленою випадковою величиною, де ймовірність успіху є\(p=\frac{1}{2N}\). Час очікування пари ліній для злиття схожий на кількість хвостів, кинутих під час очікування голови на монеті з ймовірністю голови є\(\frac{1}{2N}\), тобто якщо населення велике, ми можемо довго чекати нашої пари, щоб об'єднатись. Ми позначимо це геометричний розподіл по\(T_2 \sim \text{Geo}(1/(2N))\). Очікуваний (тобто середнє значення за багатьма тиражами) час коалесценції пари алелів тоді
\[\mathbb{E}(T_2) = 2N\]
поколінь. Ця форма до очікування випливає з того, що середнє значення геометричної випадкової величини є\(\frac{1}{p}\).
Умовні пари алелів, що об'єднуються\(t\) поколіннями тому, існують\(2t\) покоління, в яких могла відбутися мутація. Див. Рисунок\ ref {fig:pair_coal_muts} для прикладу. Якщо швидкість мутації на покоління дорівнює\(\mu\), то очікувана кількість мутацій між парою алелів, що об'єднуються\(t\) поколіннями тому, є\(2 t\mu\) (алелі пройшли через загальну кількість\(2t\) мейозів, оскільки вони останній раз поділилися спільним предок).
[рис:пара_вугілля_мути]
Таким чином, ми можемо записати очікувану кількість мутацій (\(S_2\)), що розділяють два алелі, намальовані випадковим чином від популяції, як
\[\begin{aligned} \mathbb{E}(S_2) &= \sum_{t=0}^{\infty} \mathbb{E}(S_2 | T_2=t) P(T_2=t) \nonumber\\ & =\sum_{t=0}^{\infty} 2 \mu t P(T_2=t) \nonumber\\ & =2\mu \mathbb{E}(T_2) \nonumber\\ & = 4 \mu N \end{aligned}\]
це використовує закон загального очікування (див. Додаток Рівняння\ ref {eqn:tot_exptation_def}), щоб усереднити, яка генерація нашої пари послідовностей об'єднується. Ми припустимо, що мутація досить рідкісна, що вона ніколи не відбувається в одній і тій же basepair двічі, тобто немає декількох хітів, таким чином, що ми отримуємо, щоб побачити всі події мутації, які розділяють нашу пару послідовностей. Це припущення, що повторна мутація зникає рідко в базовій парі називається i нескінченно багато сайтів припущення, яке повинно триматися якщо\(N\mu_{BP} \ll 1\), де\(\mu_{BP}\) швидкість мутації на базову пару. Таким чином, кількість мутацій між парою ділянок є спостережуваним числом відмінностей між парою послідовностей. У попередньому розділі ми позначаємо спостережувану кількість попарних відмінностей на орієнтовно нейтральних ділянках, що розділяють пару послідовностей як\(\pi\) (ми зазвичай усереднюємо це протягом декількох пар послідовностей для області). Тому за нашою простою, нейтральною, постійною моделлю чисельності населення ми очікуємо
\[\mathbb{E}(\pi) = 4 N \mu = \theta \label{eqn:pi_expectation}\]
Таким чином, ми можемо отримати емпіричну оцінку\(\theta\) від\(\pi\), назвемо це\(\widehat{\theta}_{\pi}\), встановивши\(\widehat{\theta}_{\pi}=\pi\), тобто наш спостережуваний рівень попарного генетичного різноманіття. Якщо ми маємо незалежну оцінку\(\mu\), то від встановлення\(\pi =\widehat{\theta}_{\pi} = 4N\mu\) ми можемо додатково отримати оцінку чисельності популяції\(N\), яка відповідає нашим рівням нейтрального поліморфізму. Якщо ми оцінюємо чисельність населення таким чином, ми повинні назвати її ефективною чисельністю коалесцентної популяції (\(N_e\)). Найкраще думати про\(N_{e}\) оцінку нейтрального різноманіття як довгострокову ефективну чисельність популяції для виду, але є багато застережень, які приходять разом з цим припущенням. Наприклад, минулі вузькі місця та розширення населення підводяться до єдиного числа, і тому ця оцінка\(N_{e}\) може бути не дуже репрезентативною для чисельності населення в будь-який час. Тим не менш, це не погане місце, щоб почати думати про швидкість генетичного дрейфу для нейтрального різноманіття в нашій популяції протягом тривалих періодів часу.
Давайте візьмемо хвилинку, щоб відрізнити нашу очікувану гетерозиготність (Equation\ ref {eqn:hetero}) від нашої очікуваної кількості попарних відмінностей (\(\pi\)). Наша очікувана гетерозиготність - це ймовірність того, що два алелі в локусі, відібрані з популяції випадковим чином, відрізняються один від одного. Якщо одна або кілька мутацій відбулися з моменту останнього спільного предка пари алелів, то наші послідовності будуть відрізнятися один від одного. З іншого боку, наша\(\pi\) міра відстежує середню загальну кількість відмінностей між нашими локусами. Таким чином, часто\(\pi\) є більш корисним заходом, оскільки він фіксує кількість відмінностей між послідовностями, а не лише те, чи відрізняються вони один від одного (однак для певних типів локусів, наприклад, мікросупутників, гетерозиготність часто використовується, оскільки ми зазвичай не можемо підрахувати мінімальний кількість мутацій в розумний спосіб). У разі, коли наш локус є єдиною базоюпари, дві заходи зазвичай будуть близькі один до одного, як\(H \approx \theta\) для невеликих значень\(\theta\). Наприклад, порівняння двох послідовностей випадковим чином у людини,\(\pi \approx 1/1000\) на базову пару, і ймовірність того, що конкретна базова пара відрізняється між двома послідовностями, є\(\approx 1/1000\). Однак ці дві величини починають відрізнятися один від одного, коли ми розглядаємо регіони з більш високими показниками мутації. Наприклад, якщо розглядати область 10 кб, наша швидкість мутації буде в 10 000 разів більшою, ніж у однієї базової пари. Для цієї довжини послідовності ймовірність того, що два випадково обрані гаплотипи відрізняються, досить сильно відрізняється від кількості мутаційних відмінностей між ними. (Спробуйте швидкість мутації\(10^{-8}\) на базу та чисельність населення\(10,000\) в наших розрахунках\(\E[\pi]\) і H, щоб побачити це.)

Робінсон виявив, що лисиця, що знаходиться під загрозою зникнення Каліфорнійського острова Норманд-Айленд на Сан-Ніколасі, дуже
виявила, що лисиця, що знаходиться під загрозою зникнення Каліфорнійського острова на Сан-Ніколасі, мала дуже низький рівень різноманітності (\(\pi =0.000014 \text{bp}^{-1}\)) порівняно зі своїм близьким родичем Каліфорнійським материковим сірим лисицем ( \(0.0012\text{bp}^{-1}\)).
- Припускаючи, що швидкість мутації\(2\times 10^{-8}\) на АТ, які ефективні розміри населення ви оцінюєте для цих двох популяцій?
- Чому ефективна чисельність населення лисиці острова Норманд-Айленд настільки низька? [Підказка: швидко Google Channel острівних лисиць, щоб прочитати їх історію, а також побачити, наскільки смішно милі вони.]
Своїми словами опишіть, чому час злиття пари ліній масштабується лінійно з (ефективною) чисельністю населення.
Детальніше про попарне коалесцирование та випадковість мутації
Ми виявили, що наші попарно коалесцентні часи слідували за геометричним розподілом, Equation\ ref {eqn:coal_time_dist}. Однак це передбачає дискретні покоління, і ми часто повинні були думати про популяції, яким не вистачає дискретних поколінь (тобто людей, що відтворюються у випадковий час з деяким середнім часом генерації). Використовуючи нашу експоненціальну апроксимацію, ми можемо побачити, що
\[\approx \frac{1}{2N} e^{-t/(2N)}\]
і так думати про безперервну випадкову величину, тобто ми могли б сказати, що час коалесценції пари послідовностей (\(T_2\)) приблизно експоненціально розподіляється зі швидкістю\(1/(2N)\), тобто\(T_2 \sim \text{Exp}\left( 1/(2N) \right)\). Формально ми можемо зробити це, приймаючи межу дискретного процесу більш ретельно. Докладніше про експоненціальні випадкові величини див. у Додатку Рівняння\ ref {eqn:exp_rv_def}.
Ми вивели очікувану кількість відмінностей між парою послідовностей і говорили про мінливість часу коалесценції для пари послідовностей. Процес мутації також дуже мінливий; навіть якщо дві послідовності випадково зливаються в дуже далекому минулому, вони все одно можуть бути ідентичними в сьогоденні, якщо за цей час не було мутації.
Умовно від часу коалесценції\(t\), ймовірність того, що наша пара алелів розділена\(S_2\) мутаціями, оскільки вони останній раз ділили спільного предка, є біономіально розподіленою
\[\mathbb{P}(S_2 | T_2 = t ) = {2t \choose j} \mu^{j} (1-\mu)^{2t-j}\]
тобто мутації трапляються в\(j\) поколіннях і не трапляються в\(2t-j\) поколіннях (з тим,\({2t \choose j}\) як це поєднання подій може статися). Див. додаток Рівняння\ ref {eqn:binomial_dist} для обговорення біноміального розподілу. Припускаючи\(2t-j \approx 2t\), що\(\mu \ll 1\) і що, то ми можемо наблизити ймовірність того, що у нас є\(S_2\) мутації як розподіл Пуассона:
\[\mathbb{P}(S_2 | T_2 = t ) = \frac{ (2 \mu t )^{j} e^{-2\mu t}}{j!}\]
тобто Пуассона зі середнім\(2\mu t\). Це приклад взяття біноміального розподілу до межі розподілу Пуассона, див. Додатку Рівняння\ ref {eqn:bionom_to_poiss} для більш детальної інформації. Ми не будемо багато використовувати цей результат, але він дуже корисний для роздумів про те, як імітувати процес мутації.
Процес коалесценції зразка алелей.
Зазвичай нас цікавлять не просто пари алелей, або середня попарна різноманітність. Взагалі нас цікавлять властивості різноманітності в зразках ряду алелей, витягнутих з популяції. Замість того, щоб просто слідувати за парою ліній назад, поки вони не об'єднаються, ми можемо стежити за історією зразка алелів назад через населення.
Розглянемо спочатку вибірку трьох алелей навмання з популяції. Імовірність того, що всі три алелі виберуть точно такий же родовий алель одного покоління назад, є\(\frac{1}{(2N)^2}\). Якщо\(N\) досить великий, то це дуже мала ймовірність. Таким чином, дуже малоймовірно, що наші три алелі зливаються відразу, і через мить ми побачимо, що можна з упевненістю ігнорувати такі малоймовірні події.

Імовірність того, що конкретна пара алелів знайде спільного предка в попередньому поколінні, залишається\(\frac{1}{(2N)}\). Існує три можливі пари алелів, тому ймовірність того, що жодна пара не знайде спільного предка в попередньому поколінні, становить
\[\left(1-\frac{1}{2N} \right)^3 \approx \left( 1- \frac{3}{2N} \right)\]
Роблячи це наближення, ми множимо праву сторону і ігноруємо умови\(1/N^2\) і вище (наближення Тейлора, див. Додаток Рівняння\ ref {Eqn:Taylor_exp}). Див. Рисунок\ ref {Fig:Coalescent_simulation_3} для випадкової реалізації цього процесу.
Більш загально, коли ми\(i\) відбираємо алелі, є\({i \choose 2}\) пари, тобто\(i(i-1)/2\) пари. Таким чином, ймовірність того, що жодна пара алелів у вибірці розміру не\(i\) зливається в попередньому поколінні, становить
\[\left(1-\frac{1}{(2N)} \right)^{i \choose 2} \approx \left( 1- \frac{i \choose 2}{2N}\right)\]
хоча ймовірність коалесцирования будь-якої пари є\(\approx \frac{i \choose 2}{2N}\), знову ж таки використовуючи Equation\ ref {Eqn:Taylor_exp}.
Ми можемо ігнорувати можливість того, що більше пар алелів (наприклад, триплетонів) одночасно зливаються одночасно, оскільки терміни\(\frac{1}{N^2}\) і вище можуть бути проігноровані, оскільки вони зникають рідко. Очевидно, що в розумних розмірах вибірки є набагато більше комбінацій трійок (\({i \choose 3}\)) і більш високих порядків, ніж є пари (\({i \choose 2}\)), але якщо\(i \ll N\) тоді ми з упевненістю ігноруємо ці терміни.
Коли є\(i\) алелі, ймовірність того, що ми чекаємо, поки\(t+1\) генерація, перш ніж будь-яка пара алелів зростатиметься, становить
\[\mathbb{P}(T_i =t+1) = \frac{i \choose 2}{2N}\left( 1- \frac{i \choose 2}{2N}\right)^{t} \label{eqn:T_i}\]
Таким чином, час очікування до першої коалесцентної події, поки є\(i\) лінії, є геометрично розподіленою випадковою величиною з ймовірністю успіху\(p=\frac{i \choose 2}{2N}\), яку ми позначимо
\[T_i \sim \text{Geo} \left( \frac{i \choose 2}{2N} \right).\]
Середній час очікування, поки будь-яка пара в межах нашого зразка зливається
\[\mathbb{E}( T_i) = \frac{2N}{i \choose 2} \label{eqn:E_T_i}\]
що знову випливає з середнього геометричної випадкової величини буття\(\frac{1}{p}\).
Після того, як пара алелів вперше знаходить загальний родовий алель деяку кількість поколінь ще в минулому, нам залишається лише відстежувати цей загальний родовий алель для пари, дивлячись далі в минуле. У нашому прикладі коалесцентної генеалогії для наших 3 алелів, показаних на малюнку\ ref {Fig:coalescent_simulation_3}, ми починаємо з відстеження 3 ліній, а потім випадково синій і фіолетовий злиття в чотирьох поколіннях назад. Потім ми відстежуємо лише дві лінії, червоне походження та родове походження синіх та фіолетових алелів; потім ці два зливаються, і ми знайшли нашого останнього спільного предка нашого зразка. Інший приклад з чотирма порадами показаний на малюнку\ ref {fig:coal_w_muts}; ми відстежуємо чотири лінії, потім пару coalesce, потім ми відстежуємо три лінії, потім пару coalesce, потім ми відстежуємо дві лінії, потім ця остання пара зливається, і ми знайшли найновішого спільного предка нашого зразка (плавник, кінець сцени).
Більш загально, коли пара алелів у нашому зразку\(i\) алелів зливається, ми потім переходимо до того, щоб стежити за\(i-1\) алелями назад у часі. Потім, коли пара цих\(i-1\) алелів зливається, ми тільки потім повинні слідувати\(i-2\) алелі назад. Цей процес триває, поки ми не об'єднаємося назад до зразка з двох, а звідти до одного останнього спільного предка (MRCA).
Щоб імітувати коалесцирующую генеалогію в місці для зразка\(n\) алелей, ми просто дотримуємося наступного алгоритму:
- Набір\(i=n\).
- Імітувати випадкову величину, щоб бути часом\(T_i\) до наступної коалесцентної події з\(T_i \sim \text{Exp}\left(\frac{i \choose 2}{2N} \right)\)
- Виберіть пару алелей, щоб об'єднатися випадковим чином з усіх можливих пар.
- Набір\(i=i-1\)
- Продовжуйте циклічні кроки 2-4 до тих пір\(i=1\), поки не буде знайдений найновіший загальний предок зразка.
Дотримуючись цього алгоритму, ми генеруємо реалізацію генеалогії нашого зразка.
Очікувані властивості коалесцентних генеалогій та мутацій

Очікуваний час до останнього спільного предка.
Ми спочатку розглянемо час до найсвіжішого спільного предка всього зразка (\(T_{MRCA}\)). Це
\[T_{MRCA} = \sum_{i=n}^2 T_i\]
поколінь назад, де ми підсумовуємо\(i=n\) від алелів, що відраховуються\(i=2\) назад до алелів (див. Рис.\ ref {рис:coal_w_muts}, наприклад). Оскільки наші часи злиття для різних\(i\) є незалежними, очікуваний час для останнього спільного предка
\[\mathbb{E}(T_{MRCA}) = \sum_{i=n}^2 \mathbb{E}(T_i) = \sum_{i=n}^2 2N/{i \choose 2}\]
Використовуючи те, що\(\frac{1}{i(i-1)}=\frac{1}{i-1} - \frac{1}{i}\) і трохи перестановки, ми можемо переписати це як
\[\mathbb{E}(T_{MRCA}) = 4N\left(1- \frac{1}{n} \right) \label{TMRCA_neutral}\]
Таким чином, середнє\(T_{MRCA}\) значення масштабується лінійно з чисельністю населення\(N\). Цікаво, що коли ми переходимо до більших і більших зразків (тобто\(n \gg 1\)), середній час до останнього спільного предка сходиться далі\(4N\). Те, що відбувається тут, полягає в тому, що у великих зразках наші лінії, як правило, швидко зливаються на початку і дуже скоро зливаються до набагато меншої кількості ліній.
Припустимо, що аутосомно-ефективна популяція 10000 особин (приблизно довгострокова оцінка людини) і час покоління 30 років. Який очікуваний час найостаннішому спільному предку вибірки з 20 чоловік? Що на цей раз для вибірки з 500 чоловік?
Очікуваний загальний час в генеалогії та кількість сегрегаційних сайтів.
Мутації потрапляють на конкретні родовід коалесцирующей генеалогії і передаються всім нащадкам їх роду. Крім того, за припущенням нескінченно багатьох сайтів кожна мутація створює новий сегрегаційний сайт. Процес мутації - це процес Пуассона, і чим довше певна лінія, тобто чим більше поколінь мейозів він представляє, тим більше мутацій може накопичуватися на ньому. Таким чином, загальна кількість відокремлених ділянок у вибірці є функцією загальної кількості часу в генеалогії зразка, або суми всіх довжин гілок на генеалогічному дереві\(T_{tot}\). Наша загальна кількість часу в генеалогії
\[T_{tot} = \sum_{i=n}^2 iT_i\]
оскільки, коли є\(i\) лінії, кожен вносить час\(T_i\) до загального часу (див. Рис.\ ref {рис:coal_w_muts} для прикладу). Беручи очікування загального часу в генеалогії,
\[\mathbb{E}(T_{tot}) = \sum_{i=n}^2 i \frac{2N}{{i \choose 2} } = \sum_{i=n}^2 \frac{4N}{i -1} =\sum_{i=n-1}^1 \frac{4N}{i} \label{eqn:E_T_tot}\]
ми бачимо, що наша очікувана загальна кількість часу в генеалогічних шкалах лінійно з чисельністю нашої популяції\(N\). Наша очікувана загальна кількість часу також збільшується з розміром вибірки\(n\), але робить це дуже повільно. Це знову випливає з того, що у великих зразках початкова коалесценція зазвичай відбувається дуже швидко, так що зайві зразки додають мало до загальної кількості часу в генеалогічному дереві. Вище ми бачили, що кількість мутаційних відмінностей між парою алелів, коалесценція\(T_2\) поколінь тому була Пуассоном із середнім значенням\(2 \mu T_2\), де\(2T_{2}\) загальна довжина гілки в цьому простому генеалогічному дереві 2-зразка. Мутація, яка виникає на будь-якій гілці нашої генеалогії, спричинить сегрегаційний поліморфізм у вибірці (відповідає нашому припущенню нескінченно багатьох сайтів). Таким чином, якщо загальний час в генеалогії є\(T_{tot}\), є\(T_{tot}\) покоління для мутацій. Таким чином, загальна кількість мутацій, що розділяються в нашому зразку (\(S\)), є Пуассоном із середнім\(\mu T_{tot}\). Таким чином, очікувана кількість сегрегаційних ділянок у вибірці розміру\(n\) становить
\[\mathbb{E}(S) = \mu \mathbb{E}(T_{tot}) = \sum_{i=n-1}^1 \frac{4N\mu }{i} = \theta \sum_{i=n-1}^1 \frac{1}{i} \label{eqn:seg_sites}\]
Зверніть увагу, що це зростає з розміром вибірки\(n\), хоча і дуже повільно (приблизно зі швидкістю\(\log\) розміру вибірки). Ми можемо використовувати цю формулу, щоб отримати іншу оцінку масштабованої частоти мутації населення\(\theta\), встановивши нашу спостережувану кількість сегрегаційних ділянок у вибірці (\(S\)) рівній цьому очікуванню. Ми назвемо цей оцінювач\(\widehat{\theta}_W\):
\[\widehat{\theta}_W =\frac{ S}{\sum_{i=n-1}^1 \frac{1}{i}} \label{watterson_theta}\]
Цей оцінювач\(\theta\) був розроблений, отже,\(W\).
Нейтральний сайт-частотний спектр
Ми можемо використовувати наш процес коалесценції, щоб знайти очікувану кількість похідних алелів теперішнього\(i\) часу поза розміром вибірки\(n\), наприклад, скільки синглетонів (\(i = 1\)) ми очікуємо знайти в нашому зразку? Наприклад, на рисунку\ ref {fig:coal_w_muts} у нашому зразку з чотирьох послідовностей є 3 синглетони і 2 дублетони. Кількість ділянок з цими різними частотами алелів залежить від довжини конкретних генеалогічних гілок. Мутація, яка потрапляє на гілку з\(i\) нащадками, створить похідний алель з частотою\(i\). Наприклад, у нашому прикладі дерево на малюнку\ ref {fig:coal_w_muts}, загальна кількість поколінь, де мутація може виникнути і бути подвійним\(T_3+2T_2\), дорівнює, загальна довжина гілки предка тільки помаранчевий і червоний алель\((T_3+T_2)\) плюс гілка предкова до тільки синій і фіолетовий алель\((T_2)\).
Щоб побачити, як ми могли б піти про це, давайте почнемо з розгляду простого коалесцирующего дерева, показаного на малюнку\ ref {fig:freq_coal}, для зразка\(3\) алелей, витягнутих з популяції. Мутації, що потрапляють на гілки, пофарбовані в чорний колір, будуть похідними синглетонами, тоді як мутації, що падають уздовж помаранчевої гілки, будуть дублетонами у зразку. Загальна кількість поколінь, де може виникнути однотонна мутація, становить\(3 T_3 + T_2\). Зверніть увагу, що ми рахуємо лише час, коли є дві лінії один\((T_{2})\) раз. Таким чином, наше очікуване число синглетонів, використовуючи рівняння\ ref {EQN:E_T_I}, є
\[\mathbb{E}(S_i) = \mu \left( 3\mathbb{E}(T_3) + \mathbb{E}(T_2) \right) = \mu \left( 3 \frac{2N}{3}+ 2N \right) = \theta\]
За подібною логікою час, коли можуть виникнути дублетони, є\(T_2\) і наша очікувана кількість дублетонів - це\(\mathbb{E}(S_i) =\theta/2\). Таким чином, в середньому в два рази менше дублетонів, ніж синглтонів.
Розширення цієї логіки на більші зразки може бути здійсненним, але це нудно (я маю на увазі дійсно нудно: для 10 алелів існують тисячі можливих форм дерев, і завдання швидко стає неможливим навіть обчислювальним). Приємний, відносно простий доказ спектру частот нейтрального сайту наведено, але ми не будемо давати цього тут. Загальна форма така:
\[\mathbb{E}(S_i) = \frac{\theta }{i} \label{eqn:neutral_freq_spec}\]
тобто в два рази більше синглтонів, ніж дублетонів, втричі більше синглтонів, ніж триплетонів, і так далі. Інша річ, яку нам буде корисно знати, це те, що нейтральні алелі на проміжній частоті, як правило, старі, а ті, які рідко зустрічаються у вибірці, в середньому молоді. Ми очікуємо побачити набагато більше рідкісних алелів у нашому зразку, ніж звичайні алелі.
Існує дві можливі форми дерева, які можуть стосуватися чотирьох зразків. Намалюйте обидва з них і окремо пофарбуйте (або іншим чином позначте) гілки, де можуть виникнути синглтони, дублетони та триплетонні похідні алелі.
Ми також можемо запитати ймовірність спостереження похідного алелю, що розділяється з частотою,\(i/n\) враховуючи, що сайт поліморфний у нашому зразку розміру\(n\) (тобто враховуючи це\(0<i<n\)). Цю ймовірність ми можемо отримати, розділивши очікувану кількість ділянок, що розділяються для алеля за частотою,\(i\) на очікуване число, що розділяє на всіх можливих частотах алелів для поліморфізмів у нашому зразку.
\[\begin{aligned} \mathbb{P}(i |0<i<n) &=\frac{\mathbb{E}(S_i)}{\sum_{j=1}^{n-1} \mathbb{E}(S_j)} = \frac{\frac{1}{i}}{\sum_{j=1}^{n-1} \frac{1}{j}}.\end{aligned}\]
Ми можемо інтерпретувати цю ймовірність як частку поліморфних ділянок, яку ми очікуємо знайти з частотою\(i/n\).
Тести, засновані на частотному спектрі сайту
Популяційні генетики запропонували різні способи перевірити, чи відповідає спостережуваний спектр частот сайту його нейтральним очікуванням постійного розміру. Ці тести корисні для виявлення змін чисельності населення за допомогою даних у багатьох локусах або для виявлення сигналу виділення в окремих локусах. Один з перших тестів був запропонований, і називається Tajima's\(D\). Тадзіма\(D\) є
\[D = \frac{\hat{\theta}_{\pi}-\hat{\theta}_{W}}{C} \label{eqn_Tajimas_D}\]
де чисельник - це різниця між оцінкою на\(\theta\) основі парних відмінностей і тієї, що заснована на сегрегації сайтів. Оскільки ці два оцінювачі обидва мають очікування\(\theta\) за нейтральною моделлю постійного розміру, очікування\(D\) дорівнює нулю. Знаменник\(C\) є позитивною константою; це квадратний корінь оцінки дисперсії цієї різниці при постійній чисельності населення, нейтральної моделі. Ця константа була обрана для\(D\) того, щоб мати середній нуль і\(1\) дисперсію під нульовою моделлю, тому ми можемо перевірити на відхилення від цієї простої нульової моделі.
Надлишок рідкісних алелів порівняно з нейтральною моделлю постійного розміру призведе до негативної Tajima\(D\), оскільки кожен додатковий рідкісний алель збільшує кількість сегрегаційних ділянок на\(1\), але лише має невеликий вплив на кількість парних відмінностей між зразки. На відміну від цього, позитивний Tajima\(D\) відображає перевищення алелів проміжної частоти щодо нейтрального очікування постійного розміру. Алелі на середній частоті збільшують попарну різноманітність більше на сегрегаційну ділянку, ніж типовий, тим самим збільшуючи\(\theta_{\pi}\) більше, ніж\(\theta_{W}\). У наступному розділі ми побачимо, як довгострокові зміни чисельності населення систематично змінюють частотний спектр сайту і тому виявляються статистикою, такою як Tajima\(D\).
Демографія і коалесцит
Ми вже бачили, як зміни чисельності населення можуть змінити швидкість втрати гетерозиготності від популяції (див. обговорення навколо Equation\ ref {eqn:var_pop_coal}). Якщо чисельність популяції в поколінні\(i\) є\(N_i\), ймовірність того, що пара родоводів зливається\(\frac{1}{(2N_i)}\); це відповідає нашій інтуїції, що якщо чисельність популяції невелика, швидкість, з якою пари родоводів знаходять свого спільного предка, швидше. Ми потенційно можемо пристосувати швидкі випадкові коливання чисельності населення, просто використовуючи ефективну\(N_e\) чисельність населення замість\(N\). Однак довгострокові, більш систематичні зміни чисельності населення будуть спотворювати коалесцирующіе генеалогії, а отже, і моделі різноманітності, більш систематично.

Ми бачимо, як демографія потенційно спотворює спостережуваний частотний спектр від нейтрального очікування у дуже великій вибірці людей, показаної на малюнку\ ref {Fig:human_growth}. Для порівняння, нейтральний частотний спектр Equation\ ref {eqn:neutral_freq_spec} показаний червоною лінією. Є набагато більш рідкісні алелі, ніж очікувалося за нашою нейтральною моделлю постійного розміру, але нейтральне прогнозування та реальність дещо більше погоджуються для алелів, які є більш поширеними.

Чому це? Ну, ці закономірності, ймовірно, є результатом недавнього вибухового зростання людської популяції. Якщо популяція стрімко зростала, то попарно-коалесцентний показник в минулому може бути набагато вище, ніж швидкість коалесценції ближче до теперішнього часу. (див. Рис.\ ref {рис:генеалогія_зростання}).
Одним з наслідків недавнього розширення населення є те, що генетичної різноманітності в популяції набагато менше, ніж ви могли б передбачити, використовуючи чисельність населення перепису населення. Люди є одним із прикладів цього ефекту; сьогодні нас живе\(7\) мільярд, але це пов'язано з дуже швидким зростанням населення за останні тисячо-десятки тисяч років. Наш рівень генетичного різноманіття набагато нижчий, ніж ви могли б прогнозувати, враховуючи наш розмір перепису, що відображає нашу набагато меншу популяцію предків. Другим наслідком нещодавнього розширення населення є те, що більш глибокі коалесцентні гілки набагато більше стискаються разом у часі порівняно з тими, що знаходяться в популяції постійного розміру. Мутації на більш глибоких гілках є джерелом алелів на більш проміжних частотах, і тому у зростаючих популяціях ще менше алелів середньої частоти. Ось чому в цьому великому зразку європейців так багато рідкісних алелів, особливо синглтонів.
Ще одним поширеним демографічним сценарієм є вузьке місце населення. У вузькому місці чисельність населення різко падає, а згодом відновлюється. Наприклад, наше населення, можливо, мало розмір\(N_{\textrm{Big}}\) і розбилося\(N_{\textrm{Small}}\). Один із прикладів вузького місця наведено на малюнку\ ref {fig:genealogy_crash}.

Дивлячись на вибірку ліній, взятих з населення сьогодні, якщо вузьке місце було дещо недавнім (\(\ll N_{\textrm{Big}}\)покоління в минулому), багато наших ліній не зійдуться, перш ніж досягти вузького місця, рухаючись назад у часі. Але під час вузького місця наші лінії зливаються з набагато більшою швидкістю, так що багато наших ліній будуть зливатися, якщо вузьке місце триває досить довго (\(\sim N_{\textrm{Small}}\)покоління). Якщо вузьке місце дуже сильне, то всі наші лінії будуть зливатися під час вузького місця, і результуючий спектр частот ділянки може виглядати дуже схожим на нашу модель зростання населення (тобто надлишок рідкісних алелів). Однак, якщо деякі пари ліній уникають коалесцирования під час вузького місця, вони зростуться набагато глибше у часі (наприклад, сині та помаранчеві родові лінії в\ ref {Fig:Genealogy_Crash}).
Прикладом цього є малюнок\ ref {рис:Mimulus_Bottleneck}, дані з. Mimulus nasutus - самолюбний вид, який нещодавно виник від перехрещуваного прабатька М. guttatus, і зазнав сильне вузьке місце. M. guttatus має дуже високий рівень генетичного різноманіття (\(\pi=4\%\)на синонімічних ділянках), але M. nasutus втратив значну частину цього різноманіття (\(\pi =1\%\)). Дивлячись уздовж генома, між парою хромосом M. guttatus, рівні різноманітності досить рівномірно високі.

Але при порівнянні двох хромосом M. nasutus, різноманітність низька, оскільки пара родовищ, як правило, зливається останнім часом. Проте в декількох місцях ми бачимо рівні різноманітності, порівнянні з M. guttatus; ці регіони відповідають геномним ділянкам, де наша пара ліній не може злитися під час вузького місця і згодом набагато глибше злитися в родовому M. guttatus населення.


Мутації, що виникають на більш глибоких лініях, будуть на проміжній частоті в нашому зразку, і тому м'які вузькі місця можуть призвести до перевищення алелів проміжних частот порівняно зі стандартною моделлю постійного розміру. Це може перекосити D Tajima (див. Рівняння\ ref {eqn_Tajimas_D}) в бік позитивних значень і від його очікування нуля. Один із прикладів цього перекосу наведено на малюнку\ ref {fig:maize_tajimas_d}. Кукурудза (Sea mays subsp. травня) був одомашнений від свого дикого прабатька teosinte (Zea mays subsp. parviglumis) приблизно десять тисяч років тому. Ми бачимо, як вузьке місце, пов'язане з одомашненням, призвело до втрати генетичного різноманіття кукурудзи порівняно з теосінтом, а поліморфізм, який залишається, дещо перекошений у бік проміжних частот, що призводить до більш позитивних значень D.
Voight et al. (2005) секвенував 40 аутосомних областей з 15 диплоїдних зразків людей Хауса з Яунде, Камерун. Середня довжина локусу, яку вони секвенували для кожного регіону, становила\(2365\) bp. Вони виявили, що середня кількість сегрегаційних ділянок на локус була\(S= 11.1\) і середня\(\pi = 0.0011\) на базу над локусами. D Tajima позитивний чи негативний? Чи є демографічна модель з вузьким місцем або зростанням більш відповідає цьому результату?
Резюме
- Генетичний дрейф - це випадкова зміна частот алелів через алелі випадково залишаючи більше або менше копій себе наступному поколінню. Він безспрямований, з алелями однаково ймовірно, піднімаються вгору або вниз за частотою завдяки дрейфу. Генетичний дрейф відбувається повільнішою швидкістю у більших популяціях, оскільки існує більший ступінь усереднення у більших популяціях, що зменшує вплив випадковості на розмноження людей.
- В середньому генетичний дрейф діє для видалення генетичного різноманіття (наприклад, гетерозиготності) з популяції. Швидкість втрати нейтрального генетичного різноманіття від популяції обернено пропорційна чисельності популяції.
- Баланс мутації та генетичного дрейфу може підтримувати рівноважний рівень нейтрального генетичного різноманіття в популяції. Цей рівноважний рівень визначається масштабованою популяційною швидкістю мутації (\(N \mu\)).
- На практиці генетичний дрейф рідко трапляється зі швидкістю, запропонованою чисельністю населення перепису населення, наприклад, через велику різницю в репродуктивному успіху та короткострокових коливаннях чисельності населення. У багатьох ситуаціях ми можемо вирішити цю проблему, використовуючи ефективний розмір населення замість чисельності населення перепису населення. Ми можемо оцінити цей ефективний розмір популяції, зіставивши нашу спостережувану швидкість генетичного дрейфу з очікуваною в ідеалізованій популяції.
- Ключовим розумінням мислення про закономірності нейтрального різноманіття є усвідомлення того, що нейтральні мутації не змінюють форму генетичного дерева (або генеалогії), пов'язаного з особами, і тому часто корисно спочатку подумати про дерево, а потім думати про нейтральні мутації, розкидані на вершині цього дерева.
- Теорія коалесценції описує властивості цих дерев та породжені мутаційні закономірності за моделлю нейтральної еволюції.
- Довгострокові зміни чисельності населення змінюють швидкість коалесценції передбачуваним чином, що впливає на закономірності варіації. Ці закономірності можуть бути використані для виявлення порушень моделі постійної чисельності населення та оцінки більш складних демографічних моделей.
Виходячи з музейних зразків\(\sim 1800\), ви підрахували, що середня гетерозиготність у північних слонових тюленів була\(0.0304\) через багато локусів. Виходячи з подальших зразків, ви оцінюєте, що в\(1960\) цьому впали до\(0.011\). Морські слони мають час покоління\(8\) років.
Яка ефективна чисельність населення, на яку ви оцінюєте, відповідає цьому падінню?
- Чому очікується, що великі популяції матимуть більш нейтральні варіації?
- Яка ефективна чисельність населення? Це зазвичай вище або нижче, ніж чисельність населення перепису?
- Чому ефективний розмір популяції відрізняється між аутосомами, Y-хромосомою та мтДНК?
Ви послідовно геномну область виду Бабуїнів. З 100 тисяч базових пар в середньому 200 відрізняються між кожною парою послідовностей. Припустімо, що на базову частоту мутації\(1 \times 10^{-8}\) та час генерації десять років.
- Яка ефективна чисельність населення цих бабуїнів?
- Який середній час коалесцирования (у роках) пари послідовностей у цього виду?