13.4: Приклади

Одинарна щілина

Припустимо,\ [f (x, y) =\ left\ {\ begin {масив} {l}
1\ текст {для} -а\ leq x\ leq a\\
0\ текст {для} |x|>a
\ end {масив}\ справа.\]

незалежний від\(y\). Це дійсно двовимірна проблема, тому що ми можемо зберегти\(k_{y} = 0\) і ігнорувати її (за винятком фактора\(2\pi\), про який ми не будемо турбуватися), відкинувши\(k_{y}\) інтеграл з (13.19). (13.24)\[C\left(k_{x}, k_{y}\right)=\frac{1}{4 \pi^{2}} \int d x d y f(x, y) e^{-i\left(k_{x} x+k_{y} y\right)}\]

стає (з\(2\pi\) поправкою зробити його одновимірним) ⁷\ [\ begin {зібрано}
C\ ліворуч (k_ {x}\ праворуч) =\ frac {1} {2\ pi}\ int_ {-\ infty} ^ {\ infty} d x f (x) e^ {-i k_ {x} x}\
=\ frac {1} {2\ pi}\ int_ -a} ^ {a} д х e^ {-i k_ {x} x} =\ ліворуч. \ frac {1} {-2 i\ пі k_ {x}} e^ {-i k_ {x} x}\ право|_ {-a} ^ {a} =\ frac {\ sin k_ {x} a} {\ pi k_ {x}}.
\ end {зібраний}\]

Таким чином, ми очікуємо, що інтенсивність хвилі в\(z\) цілому пропорційна\(\left|C\left(k_{x}\right)\right|^{2}\),\[I(x, y) \propto \frac{\sin ^{2}\left(k_{x} a\right)}{k_{x}^{2}}\]

де\[\frac{x}{r}=\frac{k_{x}}{k}=\frac{k_{x}}{\omega / v}\]

або\[k_{x}=\frac{\omega}{v} \frac{x}{r}.\]

Таким чином, якщо виміряти інтенсивність дифрагованого променя, відстань\(r\) від отвору, інтенсивність йде наступним чином: ⁸\[I(x, y) \propto \frac{\sin ^{2}(2 \pi a x / r \lambda)}{x^{2}}\]

де\(\lambda\) - довжина хвилі світла. Сюжет\(I\) як функції\(x\) показаний на рис\( 13.5\). Це називається дифракційною схемою. У важливому випадку світла, що проходить через невелику діафрагму, дифракційну картину можна легко спостерігати, проектуючи дифрагований промінь на екран. Особливостями цього візерунка варто відзначити великий максимум при\(x = 0\), з подвоєною шириною всіх інших максимумів, і періодичні нулі для\(x=n r \lambda / 2 a\). Зверніть увагу також, що зі\(a\) зменшенням ширини щілини розмір дифракційного малюнка збільшується.

Мораль: Це зворотне співвідношення між розміром щілини та розміром дифракційного малюнка є ще однією ілюстрацією загальної особливості перетворень Фур'є, розглянутих у главі 10.

Дифракція ближнього поля

Ми зупинимося тут, щоб обговорити область для проміжного\(z\), дифракції Френеля, де проблема дифракції є складною. Все, що ми можемо зробити, це оцінити інтеграл (13.19), чисельно, за допомогою комп'ютера, і знайти інтенсивність приблизно при різних значеннях\(z\). Наприклад, припустимо, що ми беремо\[\frac{\omega}{c}=\frac{2 \pi}{\lambda}=\frac{100}{a},\]

Малюнок\( 13.5\): Інтенсивність дифракційної картини як функція\(x\).

що відповідає досить невеликій щілині, шириною всього в\(100 / \pi \approx 32\) рази перевищує довжину хвилі. Потім ми будемо використовувати (13.19) для обчислення інтенсивності хвилі при різних значеннях\(z\), в одиницях\(a\). Для\(z\) малих результат показаний на малюнку\( 13.6\). Ви можете бачити, що основна форма променя зберігається деякий час, як ми очікували від (13.28). Однак коливання розвиваються відразу. Досить велика дифракція віглі обумовлена гострими краями. Нижче ми наведемо ще один приклад, в якому дифракція набагато м'якше. Для проміжних\(z\), показаних на малюнку\( 13.7\), коливання починають зливатися і різко змінюють загальну форму балки. При цьому пучок починає розтікатися.

Малюнок\( 13.6\): Інтенсивність хвилі, що проходить через щілину, для малих\(z\).

Нарешті, на малюнку\( 13.8\) ми показуємо підхід до великих\(z\) областей, де дифракція бере на себе повністю і з'являється дифракційна картина далекого поля (13,54).

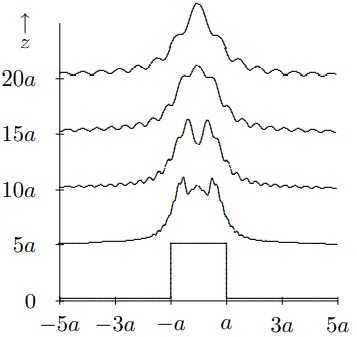
Малюнок\( 13.7\): Інтенсивність хвилі, що проходить через щілину, для проміжних\(z\).

Малюнок\( 13.8\): Інтенсивність хвилі, що проходить через щілину, так само\(z\) стає великою.

Ще один приклад може бути цікавим. Припустимо, що замість того, щоб бути простим отвором в непрозорому екрані, отвір затінено таким чином, що хвилеве порушення при\(z = 0\) має вигляд\[f(x, y)=e^{-|x| / a}.\]

Перетворення Фур'є тут було зроблено в главі 10 в (10.49) - (10.56). Підставляючи\(\omega \rightarrow k_{x}\) і\(\Gamma \rightarrow 1 / a\) в (10.56) дає\[C\left(k_{x}\right)=\frac{1}{\pi} \frac{a}{1+a^{2} k_{x}^{2}}.\]

Це визначає розподіл інтенсивності в цілому\(z\). Однак, на відміну від попереднього прикладу, цей малюнок дає дуже ніжну дифракцію. Для\(z\) малих малюнок інтенсивності показаний на малюнку\( 13.9\). Різка точка в (13,56) зникає, але в іншому випадку зміна відбувається дуже поступово, оскільки початковий візерунок дуже плавний, за винятком\(x = 0\). Для проміжних і великих\(z\), схеми інтенсивності показані на малюнку\( 13.10\) і малюнку\( 13.11\).

Малюнок\( 13.9\): Розподіл інтенсивності від (13,56) для малих\(z\).

Малюнок\( 13.10\): Розподіл інтенсивності від (13,56) для проміжних\(z\).

Малюнок\( 13.11\): Розподіл інтенсивності від (13,56) для великих\(z\).

Прямокутник

Припустимо,\ [f (x, y) -\ left\ {\ begin {масив} {l}
1\ текст {для} -a_ {x}\ leq x\ leq a_ {x}\ текст {і} -a_ {y}\ leq y\ leq a_ {y},\\
0\ текст {інакше}.
\ end {масив}\ право.\]

Це виріб єдиного розрізу візерунка в\(x\) з єдиним розрізом візерунком в\(y\). Перетворення Фур'є є добутком одновимірних перетворень Фур'є\ [\ begin {вирівняний}
C\ лівий (k_ {x}, k_ {y}\ правий) =&\ frac {1} {4\ pi^ {2}}\ int_ {-a_ {x}} ^ {a_ {x}} d x e^ {-i k_ {x}} -a_ {y}} ^ {a_ {y}} d y e^ {-i k_ {y} y}\
&=\ frac {\ sin\ ліворуч (k_ {x} a_ {x}\ праворуч)} {\ pi k_ {x}}\ frac {\ sin\ ліворуч (k_ {y} a_ {y}\ праворуч)} {\ pi k_ {y}}
\ кінець {вирівняний}\]

Таким чином, інтенсивність виглядає приблизно так:\[I(x, y) \propto \frac{\sin ^{2}\left(2 \pi a_{x} x / r \lambda\right)}{x^{2}} \frac{\sin ^{2}\left(2 \pi a_{y} y / r \lambda\right)}{y^{2}}.\]

Звичайно, ще раз, через загальні властивості перетворення Фур'є, якщо прямокутник вузький\(x\), дифракційний малюнок розкидається в\(k_{x}\), і аналогічно для\(y\).

\(\delta\)«Функції»

Коли щілина в (13,49) стає вужчою, дифракційна картина поширюється. Звичайно, інтенсивність також зменшується. Інтенсивність при\(k_{x} = 0\) пов'язана з перетворенням Фур'є\(f\) на нуль, яке є лише інтегралом\(f\) над усім\(x\). У міру того, як щілина звужується, цей інтеграл зменшується. Але припустимо, що ми збільшуємо інтенсивність вхідного пучка, як\(a\) зменшується, щоб зберегти інтенсивність максимуму дифракційної картини фіксованою. Ігноруючи\(y\) залежність, ми вимагаємо\ [f_ {a} (x) =\ left\ {\ begin {масив} {l}
\ frac {1} {2 a}\ text {для} -a\ leq x\ leq a,\\
0\ текст {для} |x|>a.
\ end {масив}\ право.\]

Межа\(f_{a}\) as насправді\(a \rightarrow 0\) не існує як функція. Вона дорівнює нулю скрізь, крім\(x = 0\). Але це йде\(\infty\) дуже швидко на\(x = 0\), так що\[\lim _{a \rightarrow 0} \int d x f_{a}(x)=1\]

Надзвичайно зручно винаходити об'єкт з цими властивостями, званий «\(\delta\)-функцією». Тобто\(\delta(x)\) має властивість, що вона дорівнює нулю крім при\(x = 0\), і що\[\int d x \delta(x)=1.\]

Насправді цей об'єкт має своєрідний математичний сенс, до тих пір, поки ви його не квадратизуєте. \(\delta\)-функціями можна маніпулювати, як звичайні функції, додаються разом, множаться на константи або гладкі\(\delta\) функції - -функції різних змінних можна навіть помножити - просто не квадрат їх! Наприклад, дельта-функцію можна помножити на звичайну неперервну функцію:\[f(x) \delta(x)=f(0) \delta(x)\]

де рівність випливає, тому що дельта-функція зникає\(x = 0\), крім at, так що значення значення\(f\) при 0 має значення.

Тепер з (13.63) і (13.64) повинно бути зрозуміло, що перетворення Фур'є\(\delta(x)\) є лише константою:\[C(k)=\frac{1}{2 \pi} \int d x e^{-i k x} \delta(x)=\frac{1}{2 \pi}.\]

Дифракційна картина для цієї речі, таким чином, дуже нудна. Відбувається рівномірне освітлення під усіма кутами.

Звичайно, у фізиці ми не можемо зробити\(\delta\) -функції. Однак\(a\), якщо в (13.61) набагато менше, ніж довжина хвилі хвилі, то це може бути також\(\delta\) -функція, тому що це має значення тільки для чого\(C(k_{x})\)\(k_{x}<k=2 \pi / \lambda\). Більші\(k_{x}\) відповідають експоненціальним хвилям, які швидко відмирають\(z\). Але для таких\(k_{x}\) продукту\(k_{x}a\) дуже мало, таким чином\[C\left(k_{x}\right)=\frac{1}{2 \pi} \frac{\sin k_{\underline{x}} a}{k_{x} a} \rightarrow \frac{1}{2 \pi}\left(1-\frac{\left(k_{\underline{x}} a\right)^{2}}{6}+\cdots\right) \approx \frac{1}{2 \pi}\]

і ми все ще отримуємо рівномірну дифракцію по всіх кутах.

Мораль:\(\delta\) -функції - це просто зручність. Коли фізики говорять про\(\delta\) -функції, вони означають (або, принаймні, вони повинні означати) функцію типу\(f_{a}(x)\), де\(a\) менше будь-якої фізичної відстані, яка важлива в проблемі. Після того, як\(a\) стає, що мало, часто легше відстежувати математику, коли ви йдете весь шлях до нефізичної межі,\(a = 0\).

Деякі властивості\(\delta\) -функцій

Перетворення Фур'є\(\delta\) -функції є комплексною експоненціальною:\[\text { if } f(x)=\delta(x-a) \text { then } C(k)=\frac{1}{2 \pi} e^{-i k a} \text { . }\]

Перетворення Фур'є комплексної експоненціальної є\(\delta\) -функцією:\[\text { if } f(x)=e^{-i \ell x} \text { then } C(k)=\delta(k-\ell).\]

\(\delta\)Функція -може бути досягнута як ліміт різними способами. Наприклад, з (13.68) ми очікуємо, що як\(a \rightarrow \infty\), перетворення Фур'є з (13.49) має наблизитися до\(\delta\) -функції:\[\lim _{a \rightarrow \infty} \frac{\sin k_{x} a}{k_{x}}=\delta\left(k_{x}\right) \text { . }\]

Вимір від двох

Використовуючи\(\delta\) -функції, ми можемо більш елегантно сказати, що мається на увазі під твердженням, яке ми зробили вище, що якщо\(f(x, y)\) не залежить від\(y\), проблема є одновимірною. Якщо ми подивимося на межу (13.58) як\(a_{y} \rightarrow \infty\), вона переходить в (13.49). Іншими словами, коли прямокутник нескінченно довгий, це щілина. У цій межі перетворення Фур'є, (13.59) переходить в\[\frac{\sin \left(k_{x} a_{x}\right)}{\pi k_{x}} \delta\left(k_{y}\right).\]

Це реальний сенс (13.50). Вона одновимірна в тому сенсі,\(k_{y}\) що застрягла на 0. Дифракції в\(y\) напрямку немає.

Багато вузьких прорізів

Цікавим застосуванням Δ-функцій є дифракційна картина для декількох вузьких щілин. Ми будемо використовувати це пізніше різними способами. Розглянемо функцію,\(f(x, y)\) форми\[\sum_{j=0}^{n-1} \delta(x-j b)\]

Малюнок\( 13.12\): Якщо\(b k_{x} / k=n \lambda\), то перешкоди конструктивні.

Малюнок\( 13.13\): Дифракційна картина для трьох вузьких прорізів.

Це описує ряд\(n\) вузьких прорізів ⁹ в\(x = 0\)\(x = b\)\(x = 2b\), і т. Д., аж до\(x = (n − 1)b\). Перетворення Фур'є (13.71) являє собою суму внесків від окремих\(\delta\) -функцій,

Малюнок\( 13.14\): Дифракційна картина для 6 вузьких прорізів.

від (13.67) і (13.68)\[C\left(k_{x}, k_{y}\right)=\delta\left(k_{y}\right) \frac{\perp}{2 \pi} \sum_{j=0}^{n-1} e^{-i j b k_{x}}.\]

Але сума є геометричним рядом, який можна зробити явно:\ [\ begin {зібрано}
\ sum_ {j=0} ^ {n-1} e^ {-i j b k_ {x}} =\ frac {1-e^ {-i n b k_ {x}}} {1-e^ {-i b k_ {x}}}\\
=\ frac {e^ {-i n б к_ {х}/2}\ ліворуч (e^ {i n b k_ {x}/2} -e^ {-i n b k_ {x}/2}\ праворуч)} {e^ {-i b k_ {x}/2}\ ліворуч (e^ {i b k_ {x}/ 2} -e^ {-i b k_ {x}/2}\ право)} =e^ {-i (n-1) b k_ {x}/2}\ frac {\ sin n b k_ {x}/2} {\ sin b k_ {x}/2}.
\ end {зібраний}\]

Таким чином, інтенсивність дифракційної картини пропорційна\[\frac{\sin ^{2} n b k_{x} / 2}{\sin ^{2} b k_{x} / 2}.\]

Для\(n = 2\), (13.74) просто\[4 \cos ^{2} \frac{b k_{x}}{2}=2\left(1+\cos b k_{x}\right).\]

Це проблема, з якої ми почали главу. Коли\(b k_{x}=2 m \pi\) для цілого числа\(m\), то хвиля з однієї щілини рухається далі, ніж хвиля від іншої\(m \lambda\), де\(\lambda=2 \pi / k\) довжина хвилі. Таким чином, для\(b k_{x}=2 m \pi\) втручання є конструктивним, як показано на малюнку 13.12.

Для більших\(n\) ми все одно отримуємо конструктивні перешкоди\(b k_{x}=2 m \pi\), але максимуми гостріші, тому що при більшій кількості щілин є більше можливостей для руйнівного втручання під іншими кутами. На рисунку\( 13.13\) та рисунку\( 13.14\) ми будуємо графік (13.74) проти\(bk_{x}\) from (−\(\pi\) to,\(3\pi\) щоб ви могли бачити два повних періоди) для\(n = 3\) і\(6\). Зверніть увагу на появу\(n − 2\) вторинних максимумів між первинними максимумами інтенсивності. До цих відносин ми повернемося, коли обговоримо дифракційні решітки.

____________________________________

⁶ Знову ж таки, це спрощено, ігноруючи ускладнення з кордонів так само, як (13.15).
⁷ Зверніть увагу,\(\sin k a / k\) що чітко визначено (\(= a\)) at\(k = 0\).
⁸ Тут ми припускаємо невеликі кути, так що\(\sin \theta \approx \tan \theta\). У нашому обговоренні дифракційних решіток нижче ми побачимо, що відбувається, коли різниця важлива.
⁹ «Вузький» тут означає вузький порівняно з довжиною хвилі світла — див. Мораль вище.