Skip to main content
LibreTexts - Ukrayinska

13.5: Згортка

  1. Last updated
  2. Save as PDF
  • Page ID
    79099

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Існує досить проста теорема, відома як теорема згортки, яка надзвичайно корисна при роботі з перетвореннями Фур'є. Припустимо, що у нас є дві функції,\(f_{1}(x)\) і\(f_{2}(x)\). Визначте функцію\(f_{1} \circ f_{2}\) наступним чином:\[f_{1} \circ f_{2}(x)=\int_{-\infty}^{\infty} d y f_{1}(x-y) f_{2}(y)\]

    Цей інтеграл буде добре визначено, якщо\(f_{1}(x)\) і\(f_{2}(x)\) падають досить швидко на нескінченності (і, звичайно, якщо вони ненульові тільки в кінцевій області\(x\)). Зверніть увагу, що\(f_{1} \circ f_{2}\) є функцією однієї змінної. Він також симетричний під обмін двома функціями, тому що шляхом простої зміни змінних\((y \rightarrow x-y)\)\[f_{1} \circ f_{2}(x)=\int_{-\infty}^{\infty} d y f_{1}(x-y) f_{2}(y)=\int_{-\infty}^{\infty} d y f_{1}(y) f_{2}(x-y)=f_{2} \circ f_{1}(x)\]

    Тепер теорема полягає в тому, що перетворення Фур'є згортки в\(2\pi\) рази є добутком перетворень Фур'є двох функцій. Доказ є негайним (всі інтеграли виконуються від -\(\infty\) до\(\infty\)):\ [\ begin {вирівняні}
    C_ {f_ {1}\ circ f_ {2}} (k) =\ frac {1} {2\ pi}\ int d x e^ {i k x} f_ {1}\ circ f_ {2} (x)\\
    = &\ frac {1} {2}}\ int д х e^ {i k x}\ int d y f_ {1} (x-y) f_ {2} (y)
    \ кінець {вирівняний}\]

    Тепер підставляємо\(x \rightarrow y+z\) і записуємо інтеграл над\(y\) і\(z\),\ [\ begin {зібрано}
    =\ frac {1} {2\ пі}\ int d z e^ {i k (y+z)}\ int d y f_ {1} (x-y) f_ {2} (y)\\
    =\ frac {1} {2\ pi}\ int d z e^ {i k z} f_ {1} (z)\ int d y e^ {i k y} f_ {2} (y) =2\ пі С_ {f_ {1}}} (k) C_ {f_ {2}} (k).
    \ end {зібраний}\]

    Двовимірний аналог (13.79) є прямим розширенням. Двовимірна згортка - це\[f_{1} \circ f_{2}(x, y)=\int d x^{\prime} d y^{\prime} f_{1}\left(x-x^{\prime}, y-y^{\prime}\right) f_{2}\left(x^{\prime}, y^{\prime}\right)\]

    \[C_{f_{1} \circ f_{2}}\left(k_{x}, k_{y}\right)=4 \pi^{2} C_{f_{1}}\left(k_{x}, k_{y}\right) C_{f_{2}}\left(k_{x}, k_{y}\right)\]

    Повторні візерунки

    Теорема згортки може бути використана для розуміння багатьох цікавих ситуацій. Розглянемо наступний дуже повчальний шаблон двох широких прорізів:\ [f (x, y) =\ left\ {\ begin {масив} {l}
    1\ текст {для} -a\ leq x\ leq a\\
    1\ text {для} -a\ leq x-b\ leq a\\
    0\ text {інакше}
    \ end {масив}\ право.

    для\(b > 2a\). Шматок викрійки показаний\( 13.15\) на малюнку для\(b = 3.5a\).

    clipboard_e0029ede73e7ad4504c928fd4e099c30c.png

    Малюнок\( 13.15\): Шматок непрозорого бар'єру з двома широкими прорізами.

    Це можна розцінювати як згортку двох функцій:\[f=f_{1} \circ f_{2}\]

    де\ [f_ {1} (x, y) =\ left\ {\ begin {масив} {l}
    1\ текст {для} -а\ leq x\ leq a\\
    0\ текст {інакше}
    \ end {масив}\ право.\]

    і\[f_{2}(x, y)=\delta(x) \delta(y)+\delta(x-b) \delta(y)\]

    f2 (х, у) = δ (х) δ (у) + δ (х − б) δ (у). Відповідні перетворення Фур'є: від (13,70) (13,84) (13,85) Cf1 (kx, ky) = sin (kxa) π kx δ (ky) (13,86) та від (13,73) Cf2 (kx, ky) = 1 4π2 cos box 2 eib−kx/2. Тепер застосування теореми згортки дає (13,87) CF1◦ f2 (kx, ky) = cos box 2 e−ibkx/2 sin (kxax) π kx δ (ky). (13,88) 13,6. ПЕРІОДИЧНИЙ f (x, y) 395 Оскільки b > 2a, це описує візерунок, який швидко коливається за шкалою, встановленою 1/b, з амплітудою, яка змінюється залежно від однієї щілини дифракційної картини, що характеризується розміром 1/a. візерунок для однієї широкої щілини (порівняйте (13,5)).

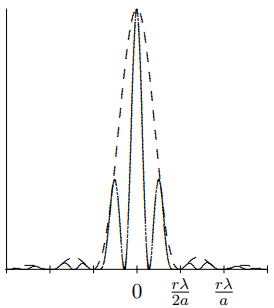
    clipboard_ee41ad75fc8be672dc64f9afb7ceef4dd.png

    Малюнок\( 13.16\): Дифракційна картина для двох широких прорізів.