8.4: Лінії електропередачі

Ми бачили, що трансляція інваріантної системи індукторів і конденсаторів може переносити хвилі. Давайте запитаємо, що відбувається, коли ми беремо межу континууму такої системи. Це дасть цікаве уявлення про електромагнітні хвилі. Співвідношення дисперсії для системи Рис\( 5.23\) задається (5.75),\[\omega^{2}=\frac{4}{L_{a} C_{a}} \sin ^{2} \frac{k a}{2} .\]

де\(L_{a}\) і\(C_{a}\) - індуктивність і ємність індукторів і конденсаторів для системи з поділом\(a\) між сусідніми частинами. Щоб взяти межу континууму, ми повинні замінити індуктивність і ємність,\(L_{a}\) і\(C_{a}\), за величинами, які ми очікуємо мати кінцеві межі як\(a \rightarrow 0\). Ми очікуємо від аналогії (5.69) між\(LC\) ланцюгами і системами пружин і мас, і обговорення на початку глави 7 про межу континууму системи мас і пружин, що відповідні величини будуть:\ [\ begin {aligned}
&\ rho_ {L}\ rightarrow\ frac { L_ {a}} {a}\ quad\ text {індуктивність на одиницю довжини}\
&K_ {a} a\ rightarrow\ frac {a} {a} {C_ {a}}\ quad\ text {ємність на одиницю довжини}
\ кінець {вирівняний}\]

Ці дві величини можна обчислити безпосередньо з індуктивності та ємності кінцевої довжини системи\(\ell\), яка містить багато окремих одиниць. Індуктивності з'єднані послідовно, тому окремі індуктивності додають, щоб дати загальну індуктивність. Таким чином, якщо довжина\(\ell\)\(na\) така, що якщо кінцева система містить\(n\) індуктори, загальна індуктивність дорівнює\(L = n L_{a}\). Тоді\[\frac{L}{\ell}=\frac{L_{a}}{a}\]

Ємності працюють однаково, оскільки вони з'єднані паралельно, а паралельні ємності додають. Таким чином\[\frac{C}{\ell}=\frac{C_{a}}{a} .\]

Тому, приймаючи ліміт\(a \rightarrow 0\) станом на (8.49), ми можемо написати\[L_{a}=a \frac{L}{\ell}, \quad C_{a}=a \frac{C}{\ell} .\]

Це дає наступне співвідношення дисперсії:\[\omega^{2}=\frac{\ell^{2}}{L C} \frac{4 \sin ^{2} \frac{k a}{2}}{a^{2}} \rightarrow \frac{\ell^{2}}{L C} k^{2} .\]

Безперервна система, подібна до цієї з фіксованою індуктивністю та ємністю на одиницю довжини, називається лінією електропередачі. Ми назвемо (8.54) відношення дисперсії для безопорної лінії електропередачі. Лінія електропередачі може використовуватися для надсилання електричних хвиль, так само, як безперервна струна передає механічні хвилі. У безперервній системі змінна зміщення, зміщений заряд, стає функцією положення вздовж лінії електропередачі. Якщо лінія електропередачі розтягнута в\(z\) напрямку, ми можемо описати заряди на лінії електропередачі функцією\(Q(z,t)\), яка є зарядом, який був зміщений через точку\(z\) на лінії електропередачі в той час\(t\). Похідна часу\(Q(z,t)\) - це струм у точці\(z\) та часі\(t\):\[I(z, t)=\frac{\partial Q(z, t)}{\partial t} .\]

Паралельна пластина лінії електропередачі

Варто опрацювати конкретний приклад ЛЕП. Приклад, який ми будемо використовувати, - це дві довгі паралельні провідні смуги. Уявіть собі нескінченну систему, в якій смуги розтягнуті паралельно один одному в площинях постійної\(y\), що йде до нескінченності в\(z\) напрямку. Припустимо, що смужки досить тонкі, щоб ми могли знехтувати їх товщиною. Припустимо далі, що ширина смуг\(w\),, набагато більше, ніж поділ,\(s\). Перетин цієї лінії електропередачі в\(x - y\) площині показано на малюнку\( 8.9\). На малюнку\(z\) напрямок виходить з площини паперу, до вас. Будемо відстежувати рух зарядів у верхньому провіднику і припустимо, що нижній провідник заземлений (при напрузі, зафіксованому при\(V = 0\)).

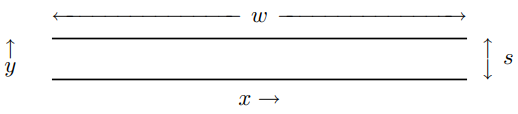
Малюнок\( 8.9\): Перетин лінії електропередачі в\(x - y\) площині.

Ми знайдемо співвідношення дисперсії лінії електропередачі, обчисливши ємність і індуктивність частини лінії довжини\(\ell\). Корисно буде зробити це з використанням енергетичних міркувань. Припустимо, що є заряд\(Q\), рівномірно поширюється по верхній пластині конденсатора, і струм\(I\), що протікає рівномірно з\(x - y\) площини в\(z\) напрямку по верхньому провіднику (і назад в площину по нижньому провіднику). Енергія, що зберігається в довжині\(\ell\), лінії електропередачі\[\frac{1}{2 C} Q^{2}+\frac{1}{2} L I^{2} ,\]

де\(C\) і\(L\) є ємність і індуктивність. ⁴

Енергія фактично зберігається в електричному і магнітному полах, що виробляються зарядом і струмом. У цій конфігурації електричне і магнітне поля майже повністю знаходяться між двома пластинами шматка лінії електропередачі. Якщо\(Q\) і\(I\) позитивні, то електричне і магнітне поля такі, як показано на малюнку\( 8.10\) і малюнку\( 8.11\). На малюнку\( 8.10\) пунктирна лінія - це перетин коробчатой області, яка може бути використана для обчислення електричного поля, використовуючи закон Гаусса. На\( 8.11\) малюнку пунктирний шлях можна використовувати для обчислення магнітного поля, використовуючи закон Ампера. Електричне і магнітне поля приблизно постійні між смугами, але швидко відпадають майже до нуля зовні.

Малюнок\( 8.10\): Електричне поле, обумовлене зарядом на лінії електропередачі.

Малюнок\( 8.11\): Магнітне поле, обумовлене струмом на лінії електропередачі.

Щільність заряду на верхній пластині приблизно рівномірна і задається загальним зарядом, поділеним на площу\(w \ell\),\[\sigma \approx \frac{Q}{w \ell} .\]

Потім можна застосувати закон Гаусса до невеликої коробчатої області, перетин якої показано на малюнку\( 8.10\) і зробити висновок, що електричне поле всередині задається\[E_{y} \approx-\frac{Q}{\epsilon_{0} w \ell}\]

Щільність енергії, що зберігається в електричному полі між пластинами, тому\[u_{E}=\frac{\epsilon_{0}}{2} E^{2} \approx \frac{Q^{2}}{2 \epsilon_{0} w^{2} \ell^{2}} .\]

Загальна енергія, накопичена в електричному полі, потім отримують\(u_{E}\) шляхом множення на обсяг між пластинами, що дає\[\frac{1}{2} \frac{s}{\epsilon_{0} w \ell} Q^{2}\]

таким чином (порівняно з (8.56))\[C=\frac{\epsilon_{0} w \ell}{s} .\]

Аналогічним чином ми можемо обчислити індуктивність. Закон Ампера, застосований до шляху, що охоплює верхній провідник (як показано на малюнку 8.11), дає\[B_{x} \approx \frac{\mu_{0} I}{w} .\]

Щільність енергії, що зберігається в магнітному полі між пластинами, тому\[u_{B}=\frac{1}{2 \mu_{0}} B^{2} \approx \frac{\mu_{0} I^{2}}{2 w^{2}} .\]

Загальна енергія, що зберігається в магнітному полі, потім отримують\(u_{B}\) шляхом множення на обсяг між пластинами, що дає\[\frac{1}{2} \frac{\mu_{0} s \ell}{w} I^{2}\]

таким чином (порівняно з (8.56))\[L=\frac{\mu_{0} s \ell}{w} .\]

Тепер ми можемо поставити (8.61) і (8.65) в (8.54), щоб отримати співвідношення дисперсії для цієї лінії електропередачі:\[\omega^{2}=\frac{1}{\mu_{0} \epsilon_{0}} k^{2}=c^{2} k^{2} ,\]

\(c\)де швидкість світла!

Хвилі в лінії електропередачі

Співвідношення дисперсії (8.66) виглядає підозріло як співвідношення дисперсії для електромагнітних хвиль. Насправді електричне і магнітне поля між смугами ЛЕП мають саме форму електромагнітної хвилі. Щоб побачити це явно, давайте подивимося на біжучу хвилю на лінії електропередачі, і розглянемо заряд\(Q(z,t)\), зміщений через\(z\), з незведеним комплексом\(t\) експоненціальної\(z\) і залежністю,\[Q(z, t)=q e^{i(k z-\omega t)} .\]

Ця хвиля рухається в позитивному\(z\) напрямку, назустріч вам на схемі малюнка\( 8.9\).

У будь-який фіксований час\(t\) та положення електричні та магнітні поля всередині лінії електропередачі виглядають так\(z\), як показано на малюнку\( 8.10\) та малюнку\( 8.11\) (або обидва можуть вказувати у зворотному напрямку). Ми можемо знайти магнітне поле так само, як ми робили вище, тому що струм в будь-якій точці вздовж лінії задається (8.55), так\[B_{x}(z, t) \approx \frac{\mu_{0} I(z, t)}{w}=\frac{\mu_{0}}{w} \frac{\partial}{\partial t} Q(z, t)=-i \frac{\mu_{0} \omega q}{w} e^{i(k z-\omega t)} .\]

Щоб знайти електричне поле як функцію\(z\) і\(t\), нам потрібна щільність заряду по лінії. Як тільки ми це отримаємо, ми можемо знайти електричне поле, використовуючи закон Гаусса, як зазначено вище. Ненульова щільність заряду виникає, якщо величина зміщеного заряду змінюється в залежності від\(z\). Найпростіше знайти щільність заряду, повернувшись в дискретну систему, розглянуту в розділі 5, і до (5.72). Мовою, якою ми позначаємо частини системи за їх положеннями, заряд\(q_{j}\), в дискретній системі стає\(q(z,t)\) куди\(z = j a\). Як\(a \rightarrow 0\), це відповідає лінійної щільності заряду уздовж лінії передачі\[\rho(z, t)=\frac{q(z, t)}{a} .\]

У цій мові (5.72) стає\[q(z, t)=Q(z, t)-Q(z+a, t) ,\]

де\(Q(z,t)\) заряд зміщений через індуктор положення\(z\) в момент часу\(t\). Поєднання (8.69) і (8.70) дає\[\rho(z, l)=\frac{Q(z, t)-Q(z+a, t)}{a} .\]

Беручи ліміт, як\(a \rightarrow 0\) дає\[\rho(z, t)=-\frac{\partial}{\partial z} Q(z, t)=-i k q e^{i(k z-\omega t)} .\]

Ця лінійна щільність заряду розподіляється по ширині верхньої смуги в лінії передачі, даючи поверхневу щільність заряду\[\sigma(z, t)=\frac{\rho(z, t)}{w}=-i \frac{k q}{w} e^{i(k z-\omega t)} .\]

Тепер електричне поле із закону Гаусса\[E_{y}=-\frac{\sigma(z, t)}{\epsilon_{0}}=i \frac{k q}{\epsilon_{0} w} e^{i(k z-\omega t)} .\]

Порівнюючи (8.68) з (8.74), можна побачити, що (8.45) задоволений, так що ця пара електричних і магнітних полів утворює частину біжить електромагнітної площини хвилі.

Те, що тут відбувається, полягає в тому, що роль зарядів і струмів в смугах лінії електропередачі полягає в обмеженні електромагнітних хвиль. Без провідників неможливо було б зробити шматок плоської хвилі, як ми побачимо набагато докладніше в главі 13.

Тим часом зверніть увагу, що до режиму з\(\omega = 0\) і\(k = 0\) потрібно ставитися обережно, як і до\(\omega = k = 0\) режиму бісерної нитки, розглянутого в главі 5. Режим, в якому зміщений заряд пропорційний\(z\) (див. (5.41)), описує ситуацію, при якій заряджається вся нескінченна лінія передачі. Це не дуже цікаво в кінцевому випадку. Однак важливий режим, який не залежить від\(z\), але збільшується з часом, пропорційний.\(t\) Це описує ситуацію, при якій по провідникам протікає постійний струм. Усередині ЛЕП, в даному випадку, знаходиться постійне магнітне поле.

____________________
⁴ Див. Холідей і Резник, частина 2.