8.3: Світло
- Page ID
- 79152
Світлові хвилі, як звукові хвилі, про які ми обговорювали в попередньому розділі, за своєю суттю є тривимірними речами. Однак, як і зі звуком, ми можемо багато сказати про світло, яке більш-менш незалежне від тривимірних деталей.
Площинні хвилі
Існує простий спосіб зосередитися лише на одному вимірі. Тобто шукати рішення, в які інші два виміри взагалі не входять. Розглянемо рівняння Максвелла у вільному просторі, з точки зору векторних полів,\(\vec{E}\) і\(\vec{B}\) описуючи електричне і магнітне поля. \ [\ почати {вирівняний}
&\ розрив {\ частковий E_ {y}} {\ частковий x} -\ розрив {\ частковий E_ {x}} {\ частковий y} =-\ частковий B_ {z}} {\ частковий t}\\
&\ розрив {\ частковий E_ {z}} {\ частковий y} -\ частковий т}\\ частковий Е_ {z}}} {\ частковий z} =-\ розрив {\ часткове B_ {x}} {\ часткове t}\\
&\ гідророзриву {\ часткове E_ {x}} {\ частковий z} -\ розрив {\ частковий E_ {z}} {\ частковий x} =-\ розрив {\ частковий B_ {y}} {\ частковий t}
\ кінець {вирівняний}\]
\ [\ почати {вирівняний}
&\ розрив {\ частковий B_ {y}} {\ частковий x} -\ частковий B_ {x}} {\ частковий y} =\ mu_ {0}\ epsilon_ {0}\ frac {\ частковий E_ {z}} {\ частковий t}\\
&\ frac {\ partial B_ {z}} {\ частковий т}\\ частковий т}\\ частковий т}\\ частковий т}} -\ розрив {\ частковий B_ {y}} {\ частковий z} =\ mu_ {0}\ epsilon_ {0}\ гідророзриву {\ частковий E_ {x}} {\ частковий t}\\
&\ розрив {\ частковий B_ {x}} {\ частковий z} -\ розрив {\ частковий B_ {z}} {\ частковий x} =\ mu_ {0}\ epsilon_ {0}\ frac {\ частковий E_ {y}} {\ частковий t}
\ кінець {вирівняний}\]
\ [\ почати {вирівняний}
&\ розрив {\ частковий E_ {x}} {\ частковий х} +\ частковий Е_ {y}} {\ частковий y} +\ частковий E_ {z}} {\ частковий z} {\ частковий z} =0\\ &\ розрив {\ частковий B_ {x}} {\ частковий х} +\ частковий z} =0\\
&\ розрив {\ частковий B_ {x}} {\ частковий х} +\ частковий z} {\ частковий Z} =0\\ &\ частковий B_ {x}}}} {\ частковий y} +\ розрив {\ частковий B_ {z}} {\ частковий z} =0
\ кінець {вирівняний}\]
де\(\epsilon_{0}\) і\(\mu_{0}\) є двома константами, званими діелектричною проникністю і проникністю порожнього простору. 3 Давайте розглянемо розв'язки цих рівнянь з частинними похідними, які включають лише функції\(z\) і\(t\). У цьому випадку речі спрощують:\[0=-\frac{\partial B_{z}}{\partial t}, \quad-\frac{\partial E_{y}}{\partial z}=-\frac{\partial B_{x}}{\partial t}, \quad \frac{\partial E_{x}}{\partial z}=-\frac{\partial B_{y}}{\partial t} ,\]
\[0=\mu_{0} \epsilon_{0} \frac{\partial E_{z}}{\partial t}, \quad-\frac{\partial B_{y}}{\partial z}=\mu_{0} \epsilon_{0} \frac{\partial E_{x}}{\partial t}, \quad \frac{\partial B_{x}}{\partial z}=\mu_{0} \epsilon_{0} \frac{\partial E_{y}}{\partial t} ,\]
\[\frac{\partial E_{z}}{\partial z}=0, \quad \frac{\partial B_{z}}{\partial z}=0 .\]
Ці рівняння мають на увазі,\(B_{z}\) що\(E_{z}\) і не залежать від\(z\) і\(t\). Оскільки ми вже припустили, що вони залежать тільки від\(z\) і\(t\), це означає, що вони є константами. Ми їх ігноруємо, тому що нас цікавлять рішення з\(t\) нетривіальністю\(z\) і залежністю. Що залишає\(x\) і\(y\) компоненти, задовольняючи (8.38) і (8.39).
Тоді, оскільки (8.38) та (8.39) є інваріантними при перекладах в\(z\) і\(t\), ми очікуємо складних експоненціальних розв'язків, у яких всі складові пропорційні\[e^{i(\pm k z-\omega t)},\]
\[E_{x}(z, t)=\varepsilon_{x}^{\pm} e^{i(\pm k z-\omega t)}, \quad E_{y}(z, t)=\varepsilon_{y}^{\pm} e^{i(\pm k z-\omega t)} ,\]
\[B_{x}(z, t)=\beta_{x}^{\pm} e^{i(\pm k z-\omega t)}, \quad B_{y}(z, t)=\beta_{y}^{\pm} e^{i(\pm k z-\omega t)} ,\]
Пряма заміна (8.42) і (8.43) на (8.38) і (8.39) дає\[\mp k \varepsilon_{y}^{\pm}=\omega \beta_{x}^{\pm}, \quad \pm k \varepsilon_{x}^{\pm}=\omega \beta_{y}^{\pm},\]
\[\mp k \beta_{y}^{\pm}=-\mu_{0} \epsilon_{0} \omega \varepsilon_{x}^{\pm}, \quad \pm k \beta_{x}^{\pm}=-\mu_{0} \epsilon_{0} \omega \varepsilon_{y}^{\pm} .\]
Як завжди, ми написали хвилю з нескоротною залежністю від часу,\(e^{-i \omega t}\). Щоб отримати реальні електричні і магнітні поля, беремо реальну частину (8.42) і (8.43). Це працює тому, що рівняння Максвелла лінійні в електричному та магнітному полах. Амплітуди і\(\varepsilon_{x}^{\pm}\) т.д. Можуть бути складними.
З (8.44) і (8.45) ви бачите, що\(\varepsilon_{y}^{\pm}\) пов'язано з\(\beta_{x}^{\pm}\) і\(\varepsilon_{x}^{\pm}\) пов'язано з\(\beta_{y}^{\pm}\). Для кожного співвідношення є два однорідних одночасних лінійних рівняння в двох невідомих. Вони узгоджені тільки в тому випадку, якщо співвідношення коефіцієнтів однакове, що має на увазі відношення між\(k\) і\(\omega\),\[k^{2}=\mu_{0} \epsilon_{0} \omega^{2} .\]
Це дисперсійне відношення,\[\omega^{2}=c^{2} k^{2}=\frac{1}{\mu_{0} \epsilon_{0}} k^{2} .\]
Фазова швидкість - це швидкість світла у вакуумі (про це нам доведеться більше сказати в розділах 10 і 11!).\(c\)
Після того, як (8.47) буде задоволений, ми можемо вирішити для\(\varepsilon^{\pm}\):\(\beta^{\pm}\)\[\beta_{y}^{\pm}=\pm \frac{1}{c} \varepsilon_{x}^{\pm}, \quad \beta_{x}^{\pm}=\mp \frac{1}{c} \varepsilon_{y}^{\pm} .\]
Ці рішення рівнянь Максвелла у вільному просторі - це електромагнітні хвилі, або світлові хвилі. Ці прості рішення, в залежності тільки від\(z\) і\(t\) є прикладом плоских хвильових рішень. Назва доречна тому, що електричні та магнітні поля в хвилі мають однакове значення всюди на кожній площині постійної\(z\), за будь-який фіксований час\(t\). Ці площини поширюються в\(\pm z\) напрямку при фазовій швидкості,\(c\).
Взагалі електромагнітні хвилі можуть поширюватися в будь-якому напрямку в тривимірному просторі. Однак електричні та магнітні поля, що складають хвилю, завжди перпендикулярні напрямку, в якому рухається хвиля і перпендикулярні один одному.
Обробка електромагнітних хвиль плоских хвиль, що рухаються у\(z\) напрямку, аналогічна нашій обробці звуку в главі 7. Там же хвиля залежала тільки від\(z\). Однак електромагнітні хвилі трохи складніші, оскільки хвильове явище залежить як від електричного, так і від магнітного полів. Причина того, що ми відклали до цього часу обговорення електромагнітних хвиль, хоча вони є одним з найважливіших прикладів хвильових явищ, полягає в тому, що відносини (8, 48) між електричним та магнітним полями залежать від напрямку, в якому хвиля рухається (\(\pm\)знак!). Набагато простіше записати рішення для хвиль, що біжать, ніж для стоячих хвиль. Навіть для простих біжучих плоских хвиль ми описали\(t\), які залежать тільки від\(z\)\(\vec{E}\) і, це співвідношення між\(\vec{B}\) і напрямком хвилі залежить від тривимірних властивостей рівнянь Максвелла. Ці питання ми розглянемо набагато докладніше в главах 11 і 12.
Інтерферометри
Однією з чудових особливостей світлових хвиль є те, що їх відносно легко розділити і зібрати заново. Ця функція використовується в багатьох оптичних пристроях, один з найпростіших
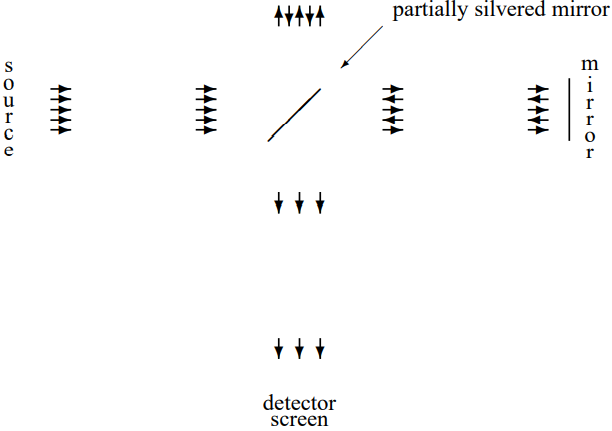
Малюнок\( 8.8\): Принципова схема інтерферометра Майкельсона.
який є «інтерферометром», один варіант якого (інтерферометр Майкельсона) показаний в схематичному вигляді на рис\( 8.8\). Джерело виробляє плоску хвилю (як ми будемо говорити в розділі 13, це не може бути досить плоска хвиля, але не забувайте, що поки що). Частково посріблене дзеркало служить «розгалужувачем променя», дозволяючи проходити частину світла, одночасно відбиваючи решту. Потім дзеркала вгорі і праворуч відображають промені назад. Тоді частково посріблене дзеркало служить «переасемблером променя», поєднуючи промені зверху і справа в єдиний промінь, який рухається на екран детектора, де вимірюється інтенсивність променя (пропорційна квадрату електричного поля). Важливим є те, що світлова хвиля, що досягає екрану детектора, є сумою двох компонентів, які є когерентними і все ж пройшли різні шляхи. Що «когерентний» означає в цьому контексті не тільки те, що частота однакова, але й те, що фаза хвиль корелюється. У цьому випадку це відбувається просто тому, що два компоненти, що досягають екрану, виникають з тієї ж вхідної площини хвилі.
Тепер інтенсивність світла, що досягає екрану, залежить від відносної довжини двох шляхів. Різна довжина шляху буде виробляти різні фази. Якщо два компоненти знаходяться в фазі, амплітуди додадуться, і екран буде яскравим. Це називається «конструктивним втручанням». Якщо два компоненти\(180^{\circ}\) поза фазою, амплітуди віднімають, а екран стане темним. Буде те, що називається «руйнівним втручанням».
Звучить це досить банально, і дійсно є (принаймні для класичних електромагнітних хвиль), але і вкрай корисно, оскільки забезпечує дуже чутливу міру змін довжини доріжок. Зокрема, якщо одне з дзеркал переміщено на відстань\(d\) (це може бути частиною експериментальної установки, призначеної для виявлення невеликих рухів, наприклад), відносна фаза двох компонентів, що досягають екрана, змінюється на те,\(2kd\) де\(k\) знаходиться кутовий номер хвилі площини хвилі, тому що довжина шляху відбитої хвилі змінилася на\(2d\). При цьому кожен раз\(d\) змінюється на чверть довжини хвилі світла, екран переходить від яскравого до темного, або навпаки.
Це дуже корисний спосіб вимірювання невеликих змін відстані. На практиці вхідний промінь - це не зовсім плоска хвиля (що, як ми детально побачимо пізніше, вимагало б нескінченного експерименту!) , тому інтенсивність світла не є рівномірною по екрану. Натомість є світлі ділянки та темні області, відомі як «бахрома». Коли дзеркало переміщується, бахрома рухається, і можна порахувати бахрому, що проходять повз даного місця, щоб відстежувати кількість змін від яскравого до темного.
Квантові перешкоди
Існує ще одна хвиля мислення про інтерферометр, яка робить його здаватися набагато менш тривіальним. Як ми кілька разів обговоримо в цій книзі, і ви дізнаєтеся більше про те, коли вивчаєте квантову механіку, світло - це не тільки хвиля. Він також складається з окремих частинок світла, званих фотонами. Ви цього не помічаєте, якщо не повернете інтенсивність світлової хвилі вниз. Але насправді ви можете зменшити інтенсивність настільки, що ви можете виявити окремі фотони, що потрапляють на екран. Тепер не так зрозуміло, що відбувається. Окремий фотон не може розділитися на дві частини на променевому розгалужувачі та розбірнику променя. Як ми побачимо пізніше, енергія фотона визначається частотою світла. Його не можна розділити. Отже, ви можете подумати, що окремий фотон повинен буде йти тим чи іншим шляхом. Але тоді як можна отримати перешкоду між двома шляхами? Немає відповіді на це питання, який має «сенс» в класичній фізиці частинок. Тим не менш, коли експеримент зроблений, кількість фотонів, що досягають екрану, залежить від різниці в довжині між двома шляхами саме так, як ви очікуєте від опису хвилі! Імовірність того, що фотон потрапить в задану пляму на екрані, пропорційна інтенсивності відповідної класичної хвилі. Якщо довжини шляху створюють руйнівні перешкоди, фотони не потрапляють. Мало того, але подібні експерименти можна проводити з іншими частинками, такими як нейтрони! Можливо, втручання не настільки тривіальне врешті-решт.
___________________________
3 Див., наприклад, Перселл, глава 9.
