5.1: Інваріантність космічного перекладу

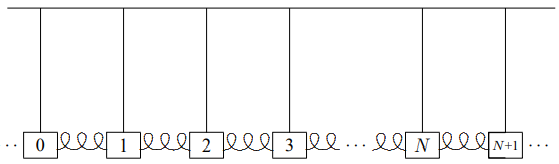
Малюнок$5.1$: Скінчена система зв'язаних маятників.

Типова система зв'язаних осциляторів, яка підтримує хвилі, є такою, як система$N$ однакових пов'язаних маятників, показана на малюнку$5.1$. Ця система є узагальненням системи двох пов'язаних маятників, яку ми вивчали в розділах 3 і 4. Припустимо, що кожен маятник боб має масу$m$, кожен маятник має довжину$\ell$, кожна пружина має постійну пружину$\kappa$ і рівноважний поділ між бобами є$a$. Припустимо далі, що тертя немає і що маятники обмежені коливатися тільки в тому напрямку, в якому натягнуті пружини. Нас цікавить вільне коливання цієї системи, без зовнішньої сили. Таке коливання, коли рух паралельно напрямку, в якому система розтягується в просторі, називається «поздовжнім коливанням». Викликати поздовжнє зміщення$j$ го боба від рівноваги (\ psi_ {j}\). Ми можемо організувати зсуви в вектор,$\Psi$ (з причин, які стануть зрозумілими нижче, це було б заплутаним у використанні$X$, тому ми вибираємо іншу букву, грецька буква psi, яка виглядає як$\psi$ у нижньому регістрі та$\Psi$ коли з великої літери):\ [\ Psi =\ left (\ begin {array} {c}
\ psi_ {1}\
\ psi_ {2}\
\ psi_ {3}\
\ vdots\\
\ psi_ {N}
\ кінець {масив}\ праворуч).\]

Тоді рівняння руху (для малих поздовжніх коливань) $$\frac{d^{2} \Psi}{d t^{2}}=-M^{-1} K \Psi$$

де$M$ діагональна матриця with$m$ вздовж діагоналі,\ [\ left (\ begin {масив} {ccccc}
m & 0 & 0 &\ cdots &
0\\ 0 & m & 0 &\ cdots &
0\\ cdots & 0\\ vdots &
\\ vdots &\ vdots &\ ddots &\\ vdots\\
0 & 0 &\ cdots & m
\ end {масив}\ праворуч),\]

і$K$ має діагональні елементи$(m g / \ell+2 \kappa)$$-\kappa$, елементи поруч з діагоналлю та нулі в іншому місці,\ [\ left (\ begin {масив} {ccccc}
m g/\ ell+2\ kappa & -\ kappa & 0\ cdots & 0\\
-\ kappa & m g/\ ell+2\ kappa &\ cdots & 0\\
0 & -\ kappa & m g/\ ell+2\ kappa &\ cdots & 0\\ vdots &
\\ vdots &\ vdots &\ ddots &\\ vdots\\
0 & 0 &\ cdots & m/\ ell+2\ kappa
\ end {масив}\ праворуч).\]

$- \kappa$У наближених до діагоналі елементи мають точно таке ж походження, як і$- \kappa$ в$2 \times 2 \text { } K$ матриці в (3.78). У ній описується зчеплення двох сусідніх блоків пружиною. $(m g / \ell+2 \kappa)$На діагоналі аналогічний$(m g / \ell+ \kappa)$ по діагоналі (3,78). Різниця в коефіцієнті 2 в коефіцієнті$\kappa$ виникає через те, що є дві пружини, по одній з кожного боку, які сприяють відновлювальному зусиллю на кожному блоці в системі, показаної на малюнку$5.1$, в той час як в системі була тільки одна, показана на малюнку$3.1$. Таким чином$M^{- 1}K$ має вигляд\ [\ left (\ begin {масив} {ccccc}
2 B & -C & 0 &\ cdots & 0\\
-C & 2 B & -C &\\ cdots &
0\\ cdots & 0\\ vdots &
\ vdots &\\ vdots &\\ dots &\ vdots\\
0 & 0 & 0 &\ cdots & 2 B
\ end {масив}\ праворуч)\]

де $$2 B=g / \ell+2 \kappa / m, \quad C=\kappa / m .$$

Цікаво порівняти матрицю (5.5) з матрицею, (4.43), з попередньої глави. В обох випадках діагональні елементи все рівні, через симетрії. Те ж саме стосується наближених до діагоналі елементів. Однак у (5.5) всі інші елементи дорівнюють нулю, оскільки взаємодія відбувається лише між найближчими сусідніми блоками. Ми називаємо такі взаємодії «локальними». У (4.43), з іншого боку, кожна з мас взаємодіє з усіма іншими. Ми будемо використовувати локальний характер взаємодій нижче.

Ми могли б спробувати знайти нормальні режими цієї системи безпосередньо, знайшовши власні вектори$M^{- 1}K$, але є набагато простіша і більш корисна техніка. Ми можемо розділити фізику системи на дві частини: фізику з'єднаних маятників та фізику стін. Для цього спочатку розглянемо нескінченну систему, яка взагалі не має стін.

Малюнок$5.2$: Шматок нескінченної системи з'єднаних маятників.

Зверніть увагу$5.2$, що на малюнку ми взагалі не змінили інтер'єр системи, зображеної$5.1$ на малюнку. Ми тільки що замінили стіни продовженням інтер'єру.

Тепер ми можемо знайти всі режими нескінченної системи Figure$5.2$ дуже легко, використовуючи аргумент симетрії. Нескінченна система Фігури$5.2$ виглядає однаково, якщо вона перекладена, переміщена вліво або вправо кратним поділу рівноваги,$a$. Він має властивість «інваріантність космічного перекладу». Інваріантність космічного перекладу — це симетрія нескінченної системи при перекладах кратними числами$a$. У цьому прикладі через дискретні блоки та скінченну довжину пружин інваріантність космічного перекладу є «дискретною». Тільки переклад інтегральними кратними$a$ дають однакову фізику. Пізніше ми обговоримо неперервні системи, які мають неперервну інваріантність космічного перекладу. Однак ми побачимо, що такі системи можна проаналізувати за допомогою тих самих методів, які ми впроваджуємо в цьому розділі.

Ми можемо використовувати симетрію інваріантності космічного перекладу, подібно до того, як ми використовували симетрії відображення та обертання, розглянуті в попередньому розділі, щоб знайти нормальні режими нескінченної системи. Дискретна космічна інваріантність перекладу нескінченної системи (симетрія при перекладах кратними$a$) дозволяє знайти нормальні режими нескінченної системи простим способом.

Більшість режимів, які ми знаходимо за допомогою інваріантності космічного перекладу нескінченної системи Figure, не$5.2$ матимуть нічого спільного з скінченною системою, показаною на рис$5.1$. Але якщо ми можемо знайти лінійні комбінації нормальних режимів нескінченної системи Фігури,$5.2$ в яких 0-й і$N$ + 1-й блоки залишаються фіксованими, то вони повинні бути розв'язками рівнянь руху системи, показаних на рис$5.1$. Причина в тому, що взаємодії між блоками є «локальними» — вони відбуваються тільки між найближчими сусідніми блоками. Таким чином, блок 1 знає, що робить блок 0, але не те, що робить блок −1. Якщо блок 0 нерухомий, він також може бути стіною, оскільки блоки з іншого боку ніяк не впливають на блок 1 (або будь-який з блоків 1 до$N$). Локальний характер взаємодії дозволяє поставити в фізику стін як граничну умову після розв'язання нескінченної задачі. Цей же трюк також дозволить нам вирішити багато інших проблем.

Давайте подивимося, як це працює для системи, показаної на малюнку$5.1$. По-перше, ми використовуємо симетрію під перекладами, щоб знайти нормальні режими нескінченної системи Figure$5.2$. Як і в попередніх двох розділах, ми описуємо розв'язки з точки зору вектора,$A$. Але тепер$A$ має нескінченну кількість компонентів,$A_{j}$ де ціле число$j$ працює від$- \infty$ до$+ \infty$. Записати цей нескінченний вектор вниз трохи незручно, але ми можемо уявити його шматок:\ [A=\ left (\ begin {масив} {c}
\ vdots\\
A_ {0}\
A_ {1}\
A_ {2}\
A_ {3}\\
\ vdots\\
A_ {N}\\
A_ {N+1}\
\ vdots
\ end {масив}\ справа).\]

Аналогічно$M^{- 1}K$ матриця для системи є нескінченною матрицею, не легко записаної, але будь-який її шматок (по діагоналі) виглядає як внутрішня частина (5.5):\ [\ left (\ begin {array} {cccccc}
\ ddots &\ vdots &\ vdots &\ vdots &\
\ ddots &\ підсилювач; 2 B & -C & 0 & 0 &\ cdots
\\\ cdots & -C & 2 B & -C & 0 &
\ cdots\\\ cdots & 0 & -C & 2 B & -C &
\\ cdots\\\ cdots\\ cdots & 0 &\\ dots &
vdots &\ vdots &\ vdots &\ ddots
\ end {масив}\ справа).\]

Ця система є «інваріантною трансляції простору», оскільки вона виглядає однаково, якщо її переміщати вліво на відстань$a$. Це переміщує блок$j+1$ туди, де$j$ раніше був блок, таким чином, якщо є режим з компонентами$A_{j}$, повинен бути інший режим з тією ж частотою, представлений вектором,\ (A^ {\ prime} = SA|), з компонентами $$A_{j}^{\prime}=A_{j+1} .$$

Матриця симетрії - це нескінченна матриця з 1s уздовж діагоналі.$S$ Вони аналогічні 1s уздовж діагоналі поруч з діагоналлю в (4.40). Однак зараз трансформація ніколи не закривається на собі. Аналога 1 в нижньому лівому куті (4.40) немає, тому що нескінченна матриця не має кута. Ми хочемо знайти власні значення та власні вектори матриці$S$, що задовольняють $$A^{\prime}=S A=\beta A$$

або еквівалентно (від (5.9)), режими в яких$A_{j}$ і$A_{j}^{\prime}$ пропорційні: $$A_{j}^{\prime}=\beta A_{j}=A_{j+1}$$

де$\beta$ деяка ненульова константа. ¹

Рівняння (5.11) можна вирішити наступним чином: Виберіть$A_{0} = 1$. Тоді$A_{1} = \beta$$A_{2} = \beta^{2}, etc., so that \(A_{j} = (\beta)^{j}$ для всіх ненегативних$j$. Ми також можемо переписати (5.11) як$A_{j-1}=\beta^{-1} A_{j}$, так що$A_{-1} = \beta_{-1$$A_{-2} = \beta_{-2}$, і т.д. таким чином рішення $$A_{j}=(\beta)^{j}$$

Тепер, коли ми знаємо форму нормальних режимів, легко отримати відповідні частоти, впливаючи на (5.12) з$M^{-1}K$ матрицею, (5.8). Це дає $$\omega^{2} A_{j}^{\beta}=2 B A_{j}^{\beta}-C A_{j+1}^{\beta}-C A_{j-1}^{\beta} ,$$

або вставлення (5.13), $$\omega^{2} \beta^{j}=2 B \beta^{j}-C \beta^{j+1}-C \beta^{j-1}=\left(2 B-C \beta-C \beta^{-1}\right) \beta^{j} .$$

Це вірно для всіх$j$, що показує, що (5.13) дійсно є власним вектором (ми вже знали це з аргументу симетрії, (4.22), але це приємно перевірити, коли це можливо), а власне значення є $$\omega^{2}=2 B-C \beta-C \beta^{-1} .$$

Зверніть увагу, що майже для кожного значення$\omega^{2}$, є два нормальних режими, тому що ми можемо обмінюватися$\beta$ і$\beta^{-1}$ без зміни (5.16). Виняток становлять лише $$\omega^{2}=2 B \mp 2 C ,$$

що відповідає$\beta=\pm 1$. Той факт, що існує не більше двох нормальних режимів для кожного значення$\omega^{2}$ матиме драматичний наслідок. Це означає, що нам доведеться мати справу лише з двома нормальними режимами одночасно, щоб реалізувати фізику кордону. Це особливість одновимірної системи, яку не поділяють дво- і тривимірні системи. Як ми побачимо, це робить одновимірну систему дуже простою в обробці.

граничні умови

5-1 Зараз
ми вирішили задачу коливання нескінченної системи. Озброївшись таким результатом, ми можемо знову занести фізику стін. Будь-який$\beta$ (крім$\beta=\pm 1$) дає пару нормальних режимів для нескінченної системи Figure$5.2$. Але тільки спеціальні значення$\beta$ будуть працювати для скінченної системи, показаної на малюнку$5.1$. Для пошуку нормальних режимів роботи системи, показаної на малюнку$5.1$, ми використовуємо (4.56), той факт, що будь-яка лінійна комбінація двох нормальних режимів з однаковою кутовою частотою$\omega$, також є нормальним режимом. Якщо ми зможемо знайти лінійну комбінацію, яка зникає для$j = 0$ і для$j = N + 1$, це буде нормальний режим системи, показаний на малюнку$5.1$. Саме зникнення нормального режиму при$j = 0$ і$j = N + 1$ є «граничними умовами» для цієї конкретної скінченної системи.

Почнемо з спроби задовольнити граничну умову при$j = 0$. Для кожного можливого значення$\omega^{2}$, ми повинні турбуватися тільки про два нормальних режими, два рішення (5.16) для$\beta$. До тих пір$\beta \neq \pm 1$, поки ми можемо знайти комбінацію, яка зникає в$j = 0$; просто відніміть два режими$A^{\beta}$ і$A^{\beta^{-1}}$ отримати вектор $$A=A^{\beta}-A^{\beta^{-1}} ,$$

або в компонентах $$A_{j} \propto A_{j}^{\beta}-A_{j}^{\beta^{-1}}=\beta^{j}-\beta^{-j} .$$

Перше, що слід помітити про (5.19), це те, що$A^{j}$ не може зникнути ні для кого,$j \neq 0$ якщо$|\beta|=1$. Таким чином, якщо ми маємо шанс задовольнити граничну умову в$j = N + 1$, ми повинні припустити, що $$\beta=e^{i \theta} .$$

Тоді з (5.19), $$A_{j} \propto \sin j \theta .$$

Тепер ми можемо задовольнити граничну умову при$j = N + 1$ встановленні$A_{N + 1} = 0$. Це має на увазі$\sin [(N+1) \theta]=0$, або $$\theta=n \pi /(N+1), \text { for integer } n .$$

Таким чином, нормальні режими системи, показані на малюнку$5.1$, є $$A_{j}^{n}=\sin \left(\frac{j n \pi}{N+1}\right), \text { for } n=1,2, \cdots N .$$

Інші значення$n$ не призводять до нових режимів, вони просто повторюють$N$ режими вже показані в (5.23). Відповідні частоти отримують шляхом введення (5.20) - (5.21) в (5.16), щоб отримати $$\omega^{2}=2 B-2 C \cos \theta=2 B-2 C \cos \left(\frac{n \pi}{N+1}\right) .$$

Звідси аналіз руху системи такий же, як і для будь-якої іншої системи зв'язаних осциляторів. Як обговорювалося в розділі 3, ми можемо розділити загальний рух і висловити його як суму нормальних режимів. Це проілюстровано для системи зв'язаних маятників в програмі 5-1 на диску програми. Нове в цій системі - це спосіб, яким ми отримали нормальні режими та їх своєрідно просту форму з точки зору тригонометричних функцій. Ми отримаємо більше розуміння значення цих режимів у наступному розділі. Тим часом зверніть увагу на спосіб, за допомогою якого прості режими можна об'єднати в дуже складний рух повної системи.

___________________
¹ Нуль не працює,$\beta$ оскільки рівняння власного значення не має рішення.