1.6: Ланцюги LC
- Page ID
- 79173
Одним з найважливіших прикладів коливальної системи є LC-схема. Ви, напевно, вивчали їх у своєму курсі на електрику та магнетизм. Як і пружина закону Гука, ця система є лінійною, оскільки відносини між зарядом, струмом, напругою тощо для ідеальних індукторів, конденсаторів та резисторів лінійні. Тут ми хочемо зробити явну аналогію між певним ланцюгом LC і системою маси на пружині. Схема LC з опором менше індуктора з індуктивністю L і конденсатором ємності С показана на малюнку 1.10. Зазвичай ми можемо взагалі не думати про це як про схему, тому що немає акумулятора або іншого джерела електроенергії. Однак ми могли собі уявити, наприклад, що конденсатор заряджався спочатку, коли ланцюг був зібраний. Тоді струм буде протікати, коли схема була завершена. Насправді, при відсутності опору струм продовжував би коливатися назавжди. Побачимо, що дана схема аналогічна комбінації пружин і маси, показаної на малюнку 1.11. Частота коливань механічної системи дорівнює
\[w=\sqrt{\frac{K}{M}}\]

Можна описати конфігурацію механічної системи цифри 1.10 через х, зміщення блоку вправо. Можна описати конфігурацію ланцюга LC малюнка 1.10 через Q, заряд, який був «витіснений» через індуктор з ситуації рівноваги з незарядженим конденсатором. В цьому випадку заряд, зміщений через індуктор, повністю йде на конденсатор, тому що йому більше нікуди йти, як показано на малюнку 1.12. Струм через індуктор є похідною за часом заряду, що пройшов,
\[I=\frac{dQ}{dt}\]
Щоб побачити, як працює схема LC, ми можемо вивчити напруги в різних точках системи, як показано на малюнку 1.13. Для індуктора падіння напруги на ньому є швидкістю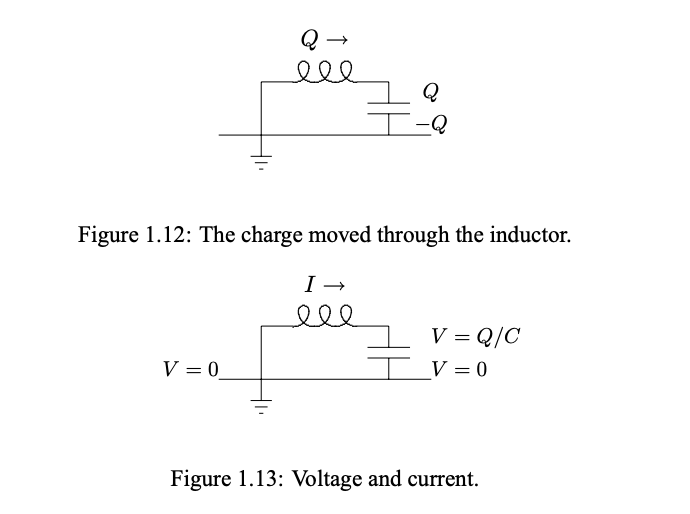
зміна струму через нього, або
\[-L\frac{dI}{dt}=V\]
Для конденсатора збережений заряд - це напруга, що перевищує ємність, або
\[V=\frac{Q}{C}\]
Складання (1.101), (1.102) і (1.103) разом дає
\[L\frac{dI}{dt}=L\frac{d^2Q}{dt^2} = -\frac{1}{C}Q\]
Відповідність двох систем полягає в наступному:

Коли ми робимо заміни в (1.105), рівняння руху (1.3) маси на пружині переходить в (1.104). Таким чином, знаючи рішення, (1.6), для маси на пружині, можна відразу зробити висновок, що зміщений заряд в цьому LC контурі коливається з частотою
\[w=\frac{1}{LC}\]
