9.1: Синусоїдальні хвилі

Last updated
Save as PDF

Page ID: 74406

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Напевно, найпростіший вид хвилі - це поперечна синусоїдальна хвиля в одновимірної струні. У такій хвилі кожна точка струни піддається гармонійному коливанню. Ми будемо називати зміщення від рівноваги\(u\), тоді ми зможемо побудувати графік\(u\) як функцію положення на струні в даний момент часу, рис. 9.2.1a, який є знімком хвилі. Крім того, ми можемо побудувати\(u\) як функцію часу для заданої точки (з заданою позицією) на рядку, Рисунок 9.2.1b. Оскільки коливання є гармонійним, зміщення як функція часу є синусоїдальною функцією, з амплітудою (максимальним зміщенням)\(A\) та періодом (час між максимумами)\(T\).

За визначенням, кожна точка струни, що зазнає синусоїдальну хвилю, зазнає гармонічного коливання, тому для кожної точки ми можемо записати\(u(t)=A \cos (\omega t+\phi)\) (Рівняння 8.1.4), де, як і раніше,\(\omega=2 \pi / T\) - (кутова) частота і\(\phi\) фаза. Дві сусідні точки на струні трохи виходять з фази - якщо хвиля рухається вправо, то ваш правий сусід досягне максимуму трохи пізніше вас, і при цьому має трохи більшу фазу. Різниця в фазі прямо пропорційна відстані між двома точками, що доходить до повної\(2 \pi\) (що, звичайно, еквівалентно нулю) після відстані\(\lambda\), довжини хвилі. Довжина хвилі це, таким чином, відстань між двома послідовними точками з однаковою фазою, зокрема між двома максимумами. Між цими максимумами фаза проходить повною мірою\(2 \pi\), тому хвиля також є синусоїдою в просторі, з «просторовою частотою» або хвильовим числом\(k=2 \pi / \lambda\). Поєднуючи залежності від простору і часу в єдиному виразі, ми можемо записати для синусоїдальної хвилі:

\[u(x, t)=A \cos (k x-\omega t) \label{9.1}\]

Малюнок\(\PageIndex{1}\): Два основних типи хвиль. (а) Поздовжня хвиля, де коливальний рух частинок знаходиться в тому ж напрямку, що і хвилі. (b) Поперечна хвиля, де коливальний рух частинок перпендикулярний руху хвилі.

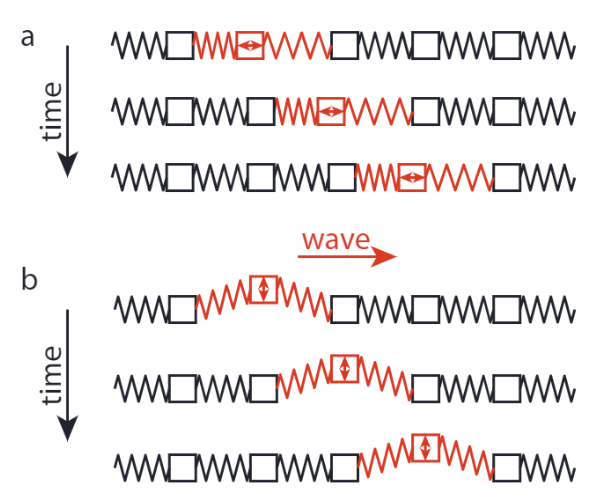
Швидкість хвилі - це відстань, яку хвиля проходить за одиницю часу. Одиниця часу для хвилі - це один період, оскільки це час, який потребує коливання, щоб повернутися до початкової точки. Відстань, пройдена за один період, становить одну довжину хвилі, оскільки це відстань між двома максимумами. Швидкість, отже, просто їх співвідношення, яке також може бути виражено через число хвиль і частоту:

\[v_{\mathrm{w}}=\frac{\lambda}{T}=\frac{\omega}{k}.\]