2.2: Графіки синусоїдальних функцій

Фокусні питання

Наступні питання призначені для керівництва нашим вивченням матеріалу в цьому розділі. Вивчивши цей розділ, ми повинні зрозуміти поняття, мотивовані цими питаннями, і вміти писати точні, узгоджені відповіді на ці питання.

Дозволяти\(A, B, C\), і\(D\) бути константи з\(B > 0\) і розглянути графік\(f(t) = A\sin(B(t - C)) + D\) або\(f(t) = A\cos(B(t - C)) + D\).

• Як значення\(A\) впливає на графік\(f\)? Як A пов'язаний з амплітудою\(f\)?
• Як значення\(B\) впливає на графік\(f\)? Як B пов'язаний з періодом\(f\)?
• Як значення\(C\) впливає на графік\(f\)?
• Як значення\(D\) впливає на графік\(f\)?
• Що робить фазовий зсув для синусоїда або косинуса графіка? Як розпізнати зсув фаз з рівняння синусоїди?
• Як ми точно намалюємо графік\(f(t) = A\sin(B(t - C)) + D\) або\(f(t) = A\cos(B(t - C)) + D\) без калькулятора і як правильно опишемо ефекти констант\(A, B, C\), причому\(D\) на графіку?

Початок діяльності

У цьому розділі ми вивчимо графіки функцій, рівняння яких є\(f(t) = A\sin(B(t - C)) + D\) і\(f(t) = A\cos(B(t - C)) + D\) де\(A, B, C\), і\(D\) є дійсними числами. Ці функції називаються синусоїдальними функціями, а їх графіки називаються синусоїдальними хвилями. Спочатку ми зупинимося на функціях, рівняннями яких є\(y = \sin(Bt)\) і\(y = \cos(Bt)\). Тепер завершіть Частина 1 або Частина 2 цієї починаючої діяльності.

Частина 1 - Використання аплету Geogebra

Щоб розпочати наше дослідження, ми будемо використовувати аплет Geogebra під назвою Період синусоїди. Веб-адреса для цього аплету http://gvsu.edu/s/LY

Після того, як ви відкриєте аплет, зверніть увагу, що у верхній частині екрана є поле введення, де ви можете ввести функцію. Наразі залиште цей набір на\(g(t) = \sin(t)\). Повинен відображатися графік синусоїдальної функції. Повзунок вгорі можна використовувати для зміни значення B. Коли це буде зроблено, графік\(y = A\sin(t)\) буде відображатися для поточного значення B разом з графіком\(y = \sin(t)\).

1. Скористайтеся повзунком, щоб змінити значення B. Детально поясніть різницю між графіком\(y = g(t) = \sin(t)\) і\(y = f(t) = \sin(Bt)\) для константи\(B > 0\). Зверніть пильну увагу на графіки і визначте період, коли\[(a)B = 2 \space (b) B = 3\space (c) B = 4 \space(d) B = 0.5\]. Зокрема, від чого залежить період\(B\)?\(y = \sin(Bt)\) Примітка: Розгляньте можливість виконання двох окремих випадків: один коли,\(B > 1\) а інший коли\(0< B <1\).
2. Тепер натисніть на кнопку скидання в правому верхньому куті екрану. Це скине значення B до початкового налаштування\(B = 1\).
3. Змініть функцію на\(g(t) = \cos(t)\) і повторіть частину (1) для функції косинуса. Чи впливає зміна значення B на графік так само, як зміна значення для B впливає на графік\(t = \sin(Bt)\)?\(y = \cos(Bt)\)

Частина 2 - Використання графічної утиліти

Переконайтеся, що ваша графічна утиліта налаштована на радіановий режим. Примітка: Більшість графічних утиліт вимагають використання\(x\) (або\(X\)) як незалежної змінної (вхідних даних) для функції. Ми будемо використовувати\(x\) для незалежної змінної, коли ми обговорюємо використання графічної утиліти.

1. Спочатку ми розглянемо графік\(y = \sin(Bx)\) для трьох різних значень\(B\). Графік три функції:\[y = \sin(x) \space\space y = \sin(2x) \space\space y = \sin(4x)\] за допомогою наступних параметрів вікна перегляду:\(0 \leq x \leq 4\pi\) і\(-1.5 \leq y \leq 1.5\). Якщо це можливо на вашій графічній утиліті, встановіть її так, щоб позначки на осі x були пробілом в\(\dfrac{\pi}{2}\) одиницях. Уважно вивчіть ці графіки і визначте період для кожної синусоїдальної хвилі. Зокрема, від чого залежить період\(B\)?\(y = \sin(Bx)\)
2. Очистіть графічний екран. Зараз ми розглянемо графік\(y = \sin(Bx)\) для трьох різних значень\(B\). Графік наступних трьох функцій:\[y = \sin(x) \space\space y = \sin(\dfrac{1}{2}x) \space\space y = \sin(\dfrac{1}{4}x)\] використовуючи наступні параметри вікна перегляду:\(0 \leq x \leq \pi\) і\(-1.5 \leq y \leq 1.5\) Якщо можливо на вашій графічній утиліті, встановіть її так, щоб позначки на осі x були розташовані в\(\dfrac{\pi}{2}\) одиницях. Уважно вивчіть ці графіки і визначте період для кожної синусоїдальної хвилі. Зокрема, як виглядає період\(y = \sin(Bx)\) залежати від B?
3. Як виглядає графік, як\(y = \sin(Bx)\) видається, пов'язаний з графіком\(y = \sin(x)\). Примітка: Розгляньте можливість виконання двох окремих випадків: один коли,\(B > 1\) а інший коли\(0 < B < 1\).

Період синусоїди

Коли ми обговорюємо такий вираз\(\cos(t)\), як\(\sin(t)\) або, ми часто посилаємося на вираз всередині дужок як аргумент функції. На початку діяльності ми розглянули ситуації, в яких аргумент був\(Bt\) за деяке число\(B\). Ми також побачили, що це число впливає на період синусоїди. Якщо ми розглядали графіки досить близько, то побачили, що період\(y = \sin(Bt)\) і\(y = \cos(Bt)\) дорівнює\(\dfrac{2\pi}{B}\). Графіки на малюнку 2.11 ілюструють це.

Зверніть увагу, що графік\(y = \sin(2t)\) має один повний цикл протягом інтервалу,\([0, \pi]\) і тому його період є\(\pi = \dfrac{2\pi}{2}\). Графік\(y = \sin(4t)\) має один повний цикл протягом інтервалу\([0, \dfrac{\pi}{2}]\) і тому його період є\(\dfrac{\pi}{2} = \dfrac{2\pi}{4}\). У цих двох випадках ми мали\(B > 1 \) в\(y = \sin(Bt)\). Чи отримуємо ми такий же результат, коли\(0 < B < 1\)? На малюнку 2.12 показані графіки для\(y = \sin(\dfrac{1}{2}t)\) і\(y = \sin(\dfrac{1}{4}t)\)?

Зверніть увагу, що графік\(y = \sin(\dfrac{1}{2}t)\) має один повний цикл протягом інтервалу\([0, 4\pi]\)

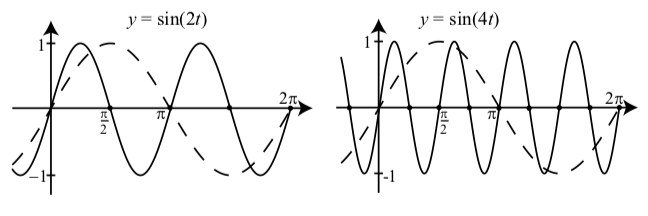
Малюнок\(\PageIndex{1}\): Графіки\(y = \sin(2t)\) і\(y = \sin(4t)\). Графік також показаний (тире).\(y = \sin(t)\)

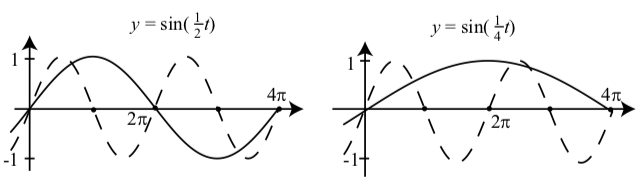
Малюнок\(\PageIndex{2}\): Графіки\(y = \sin(\dfrac{1}{2}t)\) і\(y = \sin(\dfrac{1}{4}t)\). Графік також показаний (тире).\(y = \sin(t)\)

Період\(y = \sin(\dfrac{1}{2}t)\) є\(4\pi = \dfrac{2\pi}{\dfrac{1}{2}}\).

Графік\(y = \sin(\dfrac{1}{4}t)\) має половину повного циклу протягом інтервалу\([0, 4\pi]\) і тому період\(y = \sin(\dfrac{1}{4}t)\) є\(8\pi = \dfrac{2\pi}{\dfrac{1}{4}}\).
Хорошим питанням зараз є: «Чому періоди\(y = \sin(Bt)\) і\(y = \cos(Bt)\) рівні\(\dfrac{2\pi}{B}\)?» Ідея полягає в тому, що коли ми множимо незалежну змінну\(t\) на постійну\(B\), вона може змінити вхід, який нам потрібен, щоб отримати конкретний вихід. Наприклад, вхід\(t = 0\) в\(y = \sin(t)\) і\(y = \sin(Bt)\) вихід однаковий вихід. Щоб завершити один період в\(y = \sin(Bt)\) нам потрібно пройти через інтервал довжини\(2\pi\) так, щоб наш вхід був\(2\pi\). Однак для того,\(y = \sin(Bt)\) щоб аргумент\((Bt)\) був\(2\pi\), нам потрібно\(Bt = 2\pi\) і якщо ми вирішимо це для\(t\), ми отримаємо\(t = \dfrac{2\pi}{B}\). Таким чином, функція, задана\(y = \sin(Bt)\) (або\(y = \cos(Bt)\)) завершить один повний цикл, коли\(t\) змінюється від\(t = 0\) до\(t = \dfrac{2\pi}{B}\), і, отже, період є\(\dfrac{2\pi}{B}\). Зверніть увагу, що якщо ми використовуємо\(y = A\sin(Bt)\) або\(y = A\cos(Bt)\), значення А впливає лише на амплітуду синусоїди і не впливає на період.

Якщо\(A\) є дійсним числом і\(B\) є додатним дійсним числом, то період функцій, заданих\(y = A\sin(Bt)\) і\(y = A\cos(Bt)\) є\(\dfrac{2\pi}{B}\).

Вправа\(\PageIndex{1}\)

1. Визначають амплітуду і період наступних синусоїдальних функцій:\[(a) y = 3\cos(\dfrac{1}{3}t)\]\[(b) y = -2\sin(\dfrac{\pi}{2}t)\]
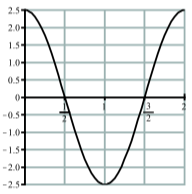
2. Графік нижче являє собою графік синусоїдальної функції. Визначте рівняння для цієї функції.

Відповідь

1. (а) Для\(y = 3\cos(\dfrac{1}{3}t)\), амплітуда є\(3\) і період є\(\dfrac{2\pi}{\dfrac{1}{3}} = 6\pi\)

(б) Для\(y = -2\sin(\dfrac{\pi}{2}t)\), амплітуда є\(2\) і період є\(\dfrac{2\pi}{\dfrac{pi}{2}} = 4\).

2. З графіка амплітуда є\(2.5\) і період є\(2\). Використовуючи функцію косинуса, ми маємо\(A = 2.5\) і\(\dfrac{2\pi}{B} = 2\). Рішення для\(B\) дарує\(B = \pi\). Таким чином, рівняння є\(y = 2.5\cos(\pi t)\).

фазовий зсув

Тепер ми будемо досліджувати ефект віднімання константи з аргументу (незалежної змінної) кругової функції. Тобто ми будемо досліджувати, який ефект значення дійсного числа\(C\) має графік\(y = \sin(t - C)\) і\(y = \cos(t - C)\).

Діяльність 2.10 (Графік\(y = \sin(t - C)\))

Завершіть частину 1 або частину 2 цієї діяльності.

Частина 1 - Використання аплету Geogebra

Ми будемо використовувати аплет Geogebra під назвою синусоїда - фазовий зсув. Веб-адреса для цього аплету http://gvsu.edu/s/Mu

Після того, як ви відкриєте аплет, зверніть увагу, що у верхній частині екрана є поле введення, де ви можете ввести функцію. Наразі залиште цей набір на\(g(t) = \sin(t)\). Повинен відображатися графік синусоїдальної функції. Повзунок вгорі можна використовувати для зміни значення C. Коли це буде зроблено, графік\(y = A\sin(t - C)\) буде відображатися для поточного значення C разом з графіком\(y = \sin(t)\).

1. Використовуйте повзунок, щоб змінити значення\(C\). Детально поясніть різницю між графіком\(y = g(t) = \sin(t)\) і\(y = f(t) = \sin(t - C)\) для константи С. зверніть пильну увагу на графіки і визначте горизонтальний\[(a) C=1\space (b) C=2\space(c) C=3\space (d) C=-1\space (e) C=-2\space (f) C=-3.\] зсув, коли Зокрема, опишіть різницю між графіком\(y = \sin(t - C)\) і графом\(y = \sin(t)\)? Примітка: Розгляньте можливість виконання двох окремих випадків: один коли,\(C >0\) а інший коли\(C < 0\).
2. Тепер натисніть на кнопку скидання в правому верхньому куті екрану. Це скине значення C до його початкового налаштування\(C = 0\).
3. Змініть функцію на\(g(t) = \cos(t)\) і повторіть частину (1) для функції косинуса. Чи впливає зміна значення С на графік впливу\(y = \cos(t - C)\) синусоїдальної хвилі так само, як зміна значення для С впливає на графік\(y = \sin(t - C)\)?

Частина 2 - Використання графічної утиліти

Переконайтеся, що ваша графічна утиліта налаштована на радіановий режим.

1. Спочатку ми розглянемо графік\(y = \sin(t - C)\) для двох різних значень\(C\). Графік три функції:\[y = \sin(x) \space y = \sin(x - 1) \space y = \sin(x - 2)\] за допомогою наступних параметрів вікна перегляду:\(0 \leq x \leq 4\pi\) і\(-1.5 \leq y \leq 1.5\). Вивчіть ці графіки уважно і опишіть різницю між графіком\(y = \sin(x - C)\) і графіком\(y = \sin(x)\) для цих значень С.
2. Очистіть графічний екран. Тепер ми розглянемо графік\(y = \sin(x - C)\) для двох різних значень C. Graph наступних трьох функцій:\[y = \sin(x)\]\[y = \sin(x + 1) = \sin(x-(-1))\]\[y = \sin(x)\]\[y = \sin(x + 2) = \sin(x-(-2))\] за допомогою наступних налаштувань вікна перегляду:\(0 \leq x \leq \pi\) і\(-1.5 \leq y \leq 1.5\). Вивчіть ці графіки уважно і опишіть різницю між графіком\(y = \sin(t - C)\) і графіком\(y = \sin(t)\) для цих значень С.
3. Опишіть різницю між графіком\(y = \sin(x - C)\) і графіком\(y = \sin(x)\)? Примітка: Розгляньте можливість виконання двох окремих випадків: один коли,\(C > 0\) а інший коли\(C < 0\).

Досліджуючи графіки в Діяльності 2.10, ми повинні помітити\(C > 0\), що коли, графік\(y = \sin(t - C)\) - це графік\(y = \sin(t)\) горизонтально перекладеного вправо одиницями C. Аналогічним чином графік\(y = \cos(t - C)\) - це графік\(y = \cos(t)\) горизонтально перекладеного вправо одиницями C. При роботі з синусоїдальним графіком такий горизонтальний переклад називається фазовим зсувом. Це проілюстровано на малюнку 2.13, на якому показані графіки\(y = \sin(t)\) і\(y = \sin(t - \dfrac{\pi}{2})\). Для довідки також\(y = \sin(t)\) наведено графік.

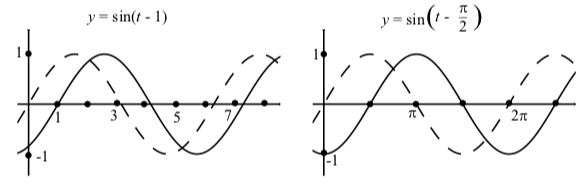
Малюнок\(\PageIndex{3}\): Графіки\(y = \sin(t - 1)\) і\(y = \sin(t - \dfrac{\pi}{2})\). Графік також показаний (тире).\(y = \sin(t)\)

Отже, чому ми спостерігаємо цей фазовий зсув? Причина полягає в тому, що графік\(y = \sin(t)\) буде проходити через один повний цикл протягом інтервалу, визначеного\(0 \leq t \leq 2\pi\). Аналогічно, графік\(y = \sin(t - C)\) буде проходити через один повний цикл протягом інтервалу, визначеного\(0 \leq t - C \leq 2\pi\). Вирішуючи для\(t\), ми бачимо, що\(C \leq t \leq 2\pi + C\). Таким чином, ми бачимо, що цей цикл для\(y = \sin(t)\) був зміщений на C одиниць.

Цей аргумент також працює, коли\(C < 0\) і коли ми використовуємо функцію косинуса замість функції синуса. Малюнок 2.14 ілюструє це за допомогою\(y = \cos(t - (-1))\) і\(y = \cos(t - (-\dfrac{\pi}{2}))\). Зверніть увагу, що ми можемо переписати ці два рівняння наступним чином:\[y = \cos(t - (-1))\]\[y = \cos(t + 1))\]\[y = \cos(t - (-\dfrac{\pi}{2}))\]\[y = \cos(t + \dfrac{\pi}{2})\]

Підсумовуємо результати для фазового зсуву наступним чином:

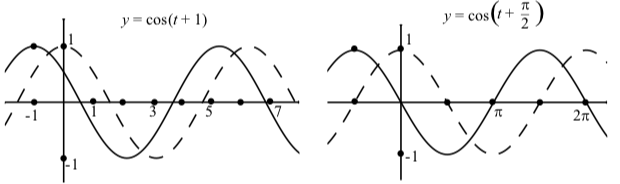
Малюнок\(\PageIndex{4}\): Графіки\(y = \cos(t + 1))\) і\(y = \cos(t + \dfrac{\pi}{2})\). Графік також показаний (тире).\[y = \cos(t)\]

Для\(y = \sin(t - C)\) і\(y = \cos(t - C)\), де C - будь-яке ненульове дійсне число:

• Графік\(y = \sin(t)\) (або\(y = \cos(t)\)) зміщений по горизонталі\(|C|\) одиниць. Це називається фазовим зсувом синусоїди.
• Якщо\(C > 0\), графік\(y = \sin(t)\) (або\(y = \cos(t)\)) зміщений по горизонталі C одиниць вправо. Тобто відбувається зсув фаз одиниць С вправо.
• Якщо\(C < 0\), графік\(y = \sin(t)\) (або\(y = \cos(t)\)) зміщений горизонтально C одиниць вліво. Тобто відбувається зсув фаз одиниць С вліво.

Вправа\(\PageIndex{2}\)

1. Визначити амплітуду і фазовий зсув наступних синусоїдальних функцій. \[(a) y = 3.2(\sin(t - \dfrac{\pi}{3})) \]\[(b) y = 4\cos(t + \dfrac{\pi}{6})\]
2. На графіку нижче наведено графік синусоїдальної функції (а) Визначити рівняння для цієї функції. (b) Визначте друге рівняння для цієї функції.

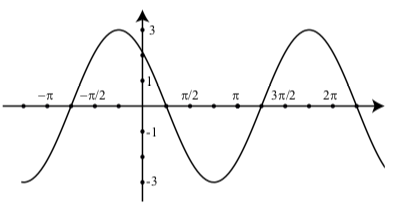
Відповідь

1. (а) Для\(y = 3.2(\sin(t - \dfrac{\pi}{3}))\), амплітуда є\(3.2\) і фазовий зсув є\(\dfrac{\pi}{3}\)
(b) Для\(y = 4\cos(t + \dfrac{\pi}{6})\), зверніть увагу, що\(y = 4\cos(t - (-\dfrac{\pi}{6}))\). Отже, амплітуда є\(4\) і фазовий зсув є\(-\dfrac{\pi}{6}\).

2. Існує кілька можливих рівнянь для цієї синусоїди. Деякі з цих рівнянь:

\[y = 3\sin(t + \dfrac{3\pi}{4})\]

\[y = -3\sin(t - \dfrac{\pi}{4})\]

\[y = 3\cos(t + \dfrac{\pi}{4})\]

\[y = -3\cos(t - \dfrac{3\pi}{4})\]

Утиліта графіків може бути використана для перевірки того, що будь-яке з цих рівнянь виробляє даний графік.

Вертикальний зсув

У нас є ще одне перетворення синусоїди для дослідження, так званий вертикальний зсув. Це один шляхом додавання константи до рівняння для синусоїди і досліджується в наступній діяльності.

Діяльність 2.12 (Вертикальний зсув синусоїди)

Завершіть частину 1 або частину 2 цієї діяльності.

Частина 1 - Використання аплету Geogebra

Зараз ми дослідимо ефект додавання константи до синусоїдальної функції. Тобто ми будемо досліджувати, який ефект значення дійсного числа\(D\) має графік\(y = A\sin(B(t - C)) + D\) і\(y = A\cos(B(t - C)) + D\). Завершіть частину 1 або частину 2 цієї діяльності. Ми будемо використовувати аплет Geogebra під назвою Вивчення синусоїди. Веб-адреса для цього аплету http://gvsu.edu/s/LX

Після того, як ви відкриєте аплет, зверніть увагу, що у верхній частині екрана є поле введення, де ви можете ввести функцію. Наразі залиште цей набір на\(g(t) = \sin(t)\). Повинен відображатися графік синусоїдальної функції. Вгорі розташовано чотири повзунки, які можна використовувати для зміни значень\(A, B, C\), і\(D\).

1. Залиште значення\(A = 1, B = 1\) і\(C = 0\) встановіть. Скористайтеся повзунком для D, щоб змінити значення C. Коли це буде зроблено, графік\(y = \sin(t) + D\) буде відображатися для поточного значення D разом з графіком\(y = \sin(t)\).

(а) За допомогою повзунка змінити значення D. докладно поясніть різницю між графіком\(y = g(t) = \sin(t)\) і\(y = f(t) = \sin(t) + D\) для константи D. Зверніть пильну увагу на графіки і визначте вертикальний зсув, коли\[i. D = 1.\]\[ii. D = 2.\]\[iii. D = 3.\]\[iv. D = -1.\]\[v. D = -2.\]\[vi. D = -3.\] Зокрема, опишіть різниця між графіком\(y = \sin(t) + D\) і графіком\(y = \sin(t)\)? Примітка: Розгляньте можливість виконання двох окремих випадків: один коли,\(D > 0\) а інший коли\(D < 0\).

(б) Тепер натисніть на кнопку скидання в правому верхньому куті екрану. Це скине значення C до його початкового налаштування\(C = 0\).

(c) Змініть функцію на\(g(t) = \cos(t)\) і повторіть частину (1) для функції косинуса. Чи впливає зміна значення D на графік впливу\(y = \cos(t) + D\) синусоїдальної хвилі так само, як зміна значення для D впливає на графік\(y = \sin(t) + D\)?

2. Тепер змініть значення A на 0,5, значення B на 2, а значення C на 0,5. Графік все одно\(g(t) = \cos(t)\) буде відображатися, але ми тепер матимемо\(f(t) = 0.5\cos(2(t - 0.5)) + D\). Чи впливає зміна значення D на графік впливу\(y = 0.5\cos(2(t - 0.5)) + D\) синусоїдальної хвилі так само, як зміна значення для D впливає на графік\(y = \cos(t)\)?

Частина 2 - Використання графічної утиліти

Переконайтеся, що ваша графічна утиліта налаштована на радіановий режим.

1. Спочатку ми розглянемо графік\(y = \cos(t) + D\) для чотирьох різних значень\(D\). Графік п'яти функцій:\[y = \cos(x)\]\[y = \cos(x) + 1\]\[y = \cos(x) - 1\]\[y = \cos(x) + 2\]\[y = \cos(x) - 2\] за допомогою наступних налаштувань вікна перегляду:\(0 \leq x \leq 2\pi\) і\(-3 \leq y \leq 3\). Вивчіть ці графіки уважно і опишіть різницю між графіком\(y = \cos(x) + D\) і графіком\(y = \cos(x)\) для цих значень D.
2. Очистіть графічний екран. Зараз ми розглянемо графік\(y = 0.5\cos(2(x - 0.5))\) для двох різних значень\(D\). Графік можна виконати наступні три функції:\[y = 0.5\cos(2(x - 0.5))\]\[y = 0.5\cos(2(x - 0.5)) + 2\]\[y = 0.5\cos(2(x - 0.5)) - 2\] за допомогою наступних параметрів вікна перегляду:\(0 \leq x \leq 2\pi\) і\(-3 \leq y \leq 3\). Вивчіть ці графіки уважно і опишіть різницю між графіком\(y = 0.5\cos(2(x - 0.5)) + D\) і графіком\(y = 0.5\cos(2(x - 0.5))\) для цих значень\(D\).

Досліджуючи графіки в Діяльності 2.12, ми повинні помітити, що графік чогось подібного\(y = A\sin(B(t - C)) + D\) є графіком\(y = A\sin(B(t - C))\) зміщених вгору\(D\) одиниць, коли\(D > 0\) і зміщений вниз\(|D|\) одиниць коли\(D < 0\). При роботі з синусоїдальним графіком такий вертикальний переклад називається вертикальним зрушенням. Це проілюстровано на малюнку 2.15 для ситуації, в якій\(D > 0\).

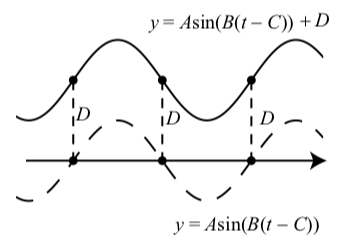
Малюнок\(\PageIndex{5}\): Графіки\(y = A\sin(B(t - C))\) (тире) і\(y = A\sin(B(t - C)) + D\) (суцільний) для\(D > 0\).

\(y\)Вісь -не показана на малюнку,\(\PageIndex{5}\) оскільки це показує загальний графік зі зсувом фази.

Те, що ми зробили в Activity 2.12, - це почати з графіка, такого як\(y = A\sin(B(t - C))\) і додати константу до залежної змінної, щоб отримати\(y = A\sin(B(t - C)) + D\). Таким чином, коли т залишається таким же, ми додаємо\(D\) до залежної змінної. Ефект полягає в тому, щоб перевести весь графік вгору на\(D\) одиниці, якщо\(D > 0\) і вниз на\(|D|\) одиниці, якщо\(D < 0\).

Амплітуда, період, фазовий зсув та вертикальний зсув

Нижче наведено короткий виклад роботи, яку ми зробили в цьому розділі, присвяченій амплітуді, періоду, зсуву фаз та вертикальному зсуву для синусоїдальної функції.

Дозволяти\(A, B, C\), і\(D\) бути ненульові дійсні числа с\(B > 0\). Для\(y = A\sin(B(t - C)) + D\) і\(y = A\cos(B(t - C)) + D\)

Амплітуда синусоїдального графіка дорівнює\(|A|\).

• Якщо\(|A| > 1\), то відбувається вертикальне розтягнення чистої синусоїди в рази\(|A|\).
• Якщо\(|A| > 1\), то відбувається вертикальне скорочення чистої синусоїди в коефіцієнт\(|A|\).

Період синусоїдального графіка дорівнює\(2\pi\).

• Коли\(B > 1\), відбувається горизонтальне стиснення графіків.
• Коли\(0 < B < 1\), є горизонтальні розтяжки графіка.

Фазовий зсув синусоїдального графіка є\(|C|\).

• Якщо\(C > 0\), відбувається горизонтальний зсув\(C\) одиниць вправо.
• Якщо\(C < 0\), відбувається горизонтальний зсув\(|C|\) одиниць вліво.

Вертикальний зсув синусоїдального графіка є\(|D|\).

• Якщо\(D > 0\), вертикальний зсув -\(D\) одиниці вгору.
• Якщо\(D < 0\), вертикальний зсув дорівнює\(|D|\) одиницям вниз.

Приклад\(\PageIndex{1}\): The Graph of a Sinusoid

Цей приклад проілюструє, як використовувати характеристики синусоїди, і послужить вступом до більш загальної дискусії, яка наступна. Графік\(y = 3\sin(4(t - \dfrac{\pi}{8})) + 2\) буде виглядати наступним чином: Зверніть увагу, що осі ще не намальовані. Ми хочемо вказати координати точок\(P, Q, R, S\), і\(T\). Є кілька варіантів, але ми зробимо точку\(P\) якомога ближче до походження. Нижче наведені важливі характеристики цієї синусоїди:

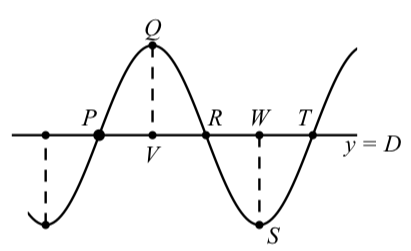
Малюнок\(\PageIndex{6}\): Графік синусоїди

• Зсув фаз є\(\dfrac{\pi}{8}\).
• Амплітуда дорівнює\(3\).
• Період - це\(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\)
• Вертикальний зсув є\(2\).

Отже, для графіка на\(\PageIndex{6}\) малюнку ми можемо зробити наступні висновки.

• Так як вертикальний зсув є\(2\), то горизонтальна лінія, яка є центральною лінією синусоїди, є\(y = 2\).
• Оскільки фазовий зсув є\(\dfrac{\pi}{8}\) і це синусоїдальна функція, координати\(P\) є\((\dfrac{\pi}{8}, 2)\).
• Оскільки період є\(\dfrac{\pi}{2}\),\(t\) -координата\(R\) є\(\dfrac{\pi}{8} + \dfrac{1}{2}(\dfrac{\pi}{2}) = \dfrac{3\pi}{8}\). Таким чином, координати\(R\) є\((\dfrac{3\pi}{8}, 2)\).
• Оскільки період є\(\dfrac{\pi}{2}\),\(t\) -координата\(T\) є\(\dfrac{\pi}{8} + \dfrac{\pi}{2} = \dfrac{5\pi}{8}\). Таким чином, координати\(R\) є\((\dfrac{5\pi}{8}, 2)\).
• Оскільки період є\(\dfrac{\pi}{2}\),\(t\) -координата\(Q\)\(\dfrac{\pi}{8} + \dfrac{1}{4}(\dfrac{\pi}{2}) = \dfrac{\pi}{4}\) є.Також, оскільки амплітуда є\(3\),\(y\) -координата\(Q\) є\(2 + 3 = 5\). Таким чином, координати\(Q\) є\((\dfrac{\pi}{4}, 5)\).
• Оскільки період є\(\dfrac{\pi}{2}\),\(t\) -координата\(S\)\(\dfrac{\pi}{8} + \dfrac{3}{4}(\dfrac{\pi}{2}) = \dfrac{\pi}{2}\) є.Також, оскільки амплітуда є\(3\),\(y\) -координата\(S\) є\(2 - 3 = -1\). Таким чином, координати\(S\) є\((\dfrac{\pi}{2}, -1)\).

Ми можемо перевірити всі ці результати за допомогою графічної утиліти, щоб намалювати графік\(y = 3\sin(4(t - \dfrac{\pi}{8})) + 2\) використання\(0 \leq t \leq \dfrac{5\pi}{8}\) і\(-2\ leq y \leq 6\). Якщо утиліта дозволяє, встановіть t-масштаб на одну чверть періоду, який є\(\dfrac{\pi}{8}\).

Важливі зауваження про синусоїди

• Для\(y = A\sin(B(t - C)) + D\) і\(y = A\cos(B(t - C)) + D\), амплітуда, період, і вертикальний зсув будуть однаковими.
• Графік для обох функцій буде виглядати так, як показано на малюнку\(\PageIndex{7}\). Різниця між\(y = A\sin(B(t - C)) + D\) і\(y = A\cos(B(t - C)) + D\) буде фазовим зсувом.
• Показана горизонтальна лінія не є віссю t. Це горизонтальна лінія\(y = D\), яку ми часто називаємо центральною лінією для синусоїди.

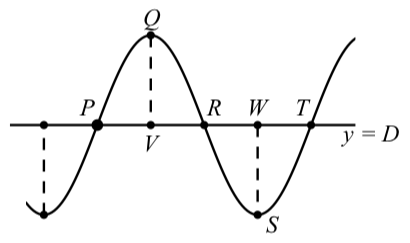
Малюнок\(\PageIndex{7}\): Графік синусоїди

Отже, щоб використовувати результати про синусоїди та рис\(\PageIndex{7}\), ми маємо:

1. Амплітуда, яку ми будемо називати підсилювачем, дорівнює довжинам відрізків\(QV\) і\(WS\).

2. Період, який ми будемо називати per, дорівнює\(\dfrac{2\pi}{B}\). Крім того, довжина\(PV,VR,RW\)\(WT\) відрізків дорівнює і\(\dfrac{1}{4} per\).
3. Для\(y = A\sin(B(t - C)) + D\), ми можемо використовувати точку\(P\) для зсуву фаз. Таким чином,\(t\) -координата точки\(P\) є\(C\) і\(P\) має координати\((C, D)\). Ми можемо визначити координати інших точок за потребою, використовуючи амплітуду та період. Наприклад:

   Точка\(Q\) має координати\((C + \dfrac{1}{4} per, D + amp)\)

   Точка\(R\) має координати\((C + \dfrac{1}{2} per, D)\)

   Точка\(S\) має координати\((C + \dfrac{3}{4} per, D - amp)\)

   Точка\(T\) має координати\((C + per, D)\)

4. Для\(y = A\cos(B(t - C)) + D\), ми можемо використовувати точку\(Q\) для зсуву фаз. Таким чином,\(t\) -координата точки\(Q\) є\(C\) і\(Q\) має координати\((C, D + amp)\). Ми можемо визначити координати інших точок за потребою, використовуючи амплітуду та період. Наприклад:

   Точка\(P\) має координати\((C - \dfrac{1}{4} per, D)\)

   Точка\(R\) має координати\((C + \dfrac{1}{4} per, D)\)

5. Точка\(S\) має координати\((C + \dfrac{1}{2} per, D - amp)\)

   Точка\(T\) має координати\((C + \dfrac{3}{4} per, D)\)

Зверніть увагу, що необов'язково намагатися запам'ятати всі факти в пунктах (3) і (4). Ми повинні пам'ятати, як використовувати поняття однієї чверті періоду та амплітуду, проілюстровану в пунктах (3) та (4). Це буде зроблено в наступних двох перевірках прогресу, на які в реальності керуються прикладами.

Вправа\(\PageIndex{3}\)

Характеристики синусоїди можуть бути корисними для встановлення відповідного вікна перегляду при створенні корисного графіка синусоїди на графічній утиліті. Особливо це актуально, коли період невеликий або великий. Для прикладу розглянемо синусоїдальну функцію\[y = 6.3\cos(50\pi(t + 0.01)) + 2\]

1. Яка амплітуда?

2. Що таке зсув фаз?

3. Що таке період?

4. Що таке вертикальний зсув?

5. Використовуйте цю інформацію для визначення координат точки на\(Q\) наступній схемі.

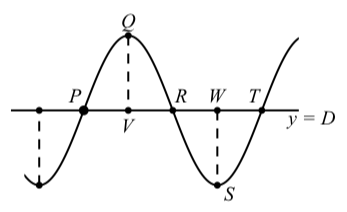
6. Тепер визначаємо координати точок\(P, R, S\), і\(T\).

7. Використовуйте цю інформацію та графічну утиліту, щоб намалювати графік (трохи більше) одного періоду цієї синусоїди, який показує точки\(P, Q\), і\(T\).

Відповідь

1. Амплітуда дорівнює\(6.3\).
2. Період - це\(\dfrac{2\pi}{50\pi} = \dfrac{1}{25}\)
3. Пишемо\(y = 6.3\cos(50\pi(t - (-0.01))) + 2\) і бачимо, що зсув фаз є\(-0.01\) або\(0.01\) одиниці вліво.
4. Вертикальний зсув є\(2\).
5. Оскільки ми використовуємо косинус і фазовий зсув є\(-0.01\), ми можемо використовувати\(-0.01\) як\(t\) -координата\(Q\). \(y\)-координата буде вертикальним зсувом плюс амплітуда. Таким чином,\(y\) -координата є\(8.3\). Точка\(Q\) має координати\((-0.01, 8.3)\)
6. Тепер ми використовуємо той факт, що відстань по горизонталі між\(P\) і\(Q\) становить одну чверть періоду. Оскільки період є\(\dfrac{1}{25} = 0.04\), ми бачимо, що одна чверть періоду становить\(0.01\). Точка\(P\) також лежить на центральній лінії, яка є\(y = 2\). Таким чином, координати\(P\) є\((-0.02, 2)\).

Тепер ми використовуємо той факт, що відстань по горизонталі між\(Q\) і\(R\) становить одну чверть періоду. Точка\(R\) знаходиться на центральній лінії синусоїди і так\(R\) має координати\((0, 2)\).

Точка\(S\) є низькою точкою на синусоїді. Так його\(y\) -координата буде\(D\) мінус амплітуда, яка є\(2 - 6.3 = -4.3\). Використовуючи той факт, що відстань по горизонталі від\(R\) до\(S\) становить одну чверть періоду, координати\(S\) є\((0.01, -4.3)\). Оскільки точка\(T\) знаходиться на центральній лінії, а горизонтальна відстань від\(S\) до\(T\) становить одну чверть періоду, координати\(T\) є\((0.03, 2)\).

7. Ми будемо використовувати оглядове вікно, яке становить одну чверть періоду ліворуч від\(P\) і одну чверть періоду праворуч від\(T\). Так ми будемо використовувати\ (-0.03

leq t\ leq 0,03\). Так як максимальне значення є,\(8.3\) а мінімальне значення є\(-4.3\), ми будемо використовувати\(-5 \leq y \leq 9\).

Вправа\(\PageIndex{4}\)

Визначимо два рівняння для синусоїди, показаних на малюнку\(\PageIndex{8}\).

1. Визначте координати точок\(Q\) і\(R\). Відстань по вертикалі між цими двома точками дорівнює двократній амплітуді. Використовуйте y-координати цих точок, щоб визначити два рази амплітуду, а потім амплітуду.
2. Центральна лінія для синусоїди знаходиться на півдорозі між високою точкою\(Q\) і низькою точкою\(R\). Використовуйте y-координати\(Q\) і\(R\) для визначення центральної лінії\(y = D\). Це буде вертикальний зсув.

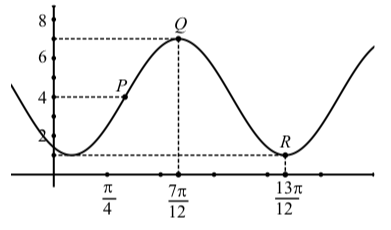
Малюнок\(\PageIndex{8}\): Графік синусоїди

3. Горизонтальна відстань між\(Q\) і\(R\) дорівнює половині періоду. Використовуйте\(R\) t-координати\(Q\) і для визначення довжини половини періоду і, отже, періоду. Скористайтеся цим, щоб визначити значення\(B\).
4. Ми зараз знайдемо рівняння виду\(y = A\cos(B(t - C)) + D\). Нам ще потрібен зсув фаз\(C\). Використовуйте точку\(Q\) для визначення фазового зсуву і, отже, значення\(C\). Тепер у нас є значення для\(A, B, C\), і\(D\) для рівняння\(y = A\cos(B(t - C)) + D\).
5. Щоб визначити рівняння виду\(y = A\sin(B(t - C')) + D\), скористаємося точкою\(P\) для визначення зсуву фаз\(C'\). (Використовувався інший символ, оскільки\(C'\) буде відрізнятися\(C\) від частини (4).) Зверніть увагу, що y-координата\(P\) дорівнює 4 і так\(P\) лежить на центральній лінії. Ми можемо використовувати той факт, що відстань по горизонталі між P і\(Q\) дорівнює одній чверті періоду. Визначте t координату\(P\), яка буде дорівнює\(C'\). Тепер пишемо рівняння\(y = A\sin(B(t - C')) + D\). використовуючи значення\(A, B, C'\), і\(D\) що ми визначили.

Ми можемо перевірити рівняння, які ми знайшли в частинок (4) і (5), побудувавши ці рівняння за допомогою графічної утиліти.

Відповідь

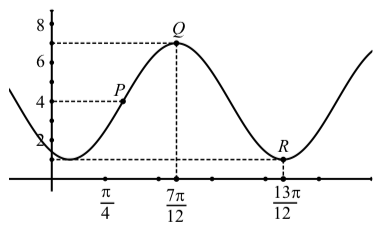
1. Координати\(Q\) є\((\dfrac{7\pi}{12}, 7)\) і координати\(R\) є\((\dfrac{13\pi}{12}, 1)\). Так що два рази амплітуда\(7 - 1 = 6\) і амплітуда є\(3\).

2. Додаємо амплітуду до\(y\) найнижчого -значення для визначення\(D\). Це дає\(D = 1 + 3 = 4\) і центральна лінія\(y = 4\).

3. Відстань по горизонталі між\(Q\) і\(R\) є\(\dfrac{13\pi}{12} - \dfrac{7\pi}{12} = \dfrac{6\pi}{12}\). Таким чином, ми бачимо, що половина періоду є\(\dfrac{\pi}{2}\) і період є\(\pi\). Отже\(B = \dfrac{2\pi}{\pi} = 2\).

4. Для\(y = A\cos(B(t - c)) + D\), ми можемо використовувати точку\(Q\) для визначення фазового зсуву\(\dfrac{7\pi}{12}\). Отже, рівняння для цієї синусоїди\[y = 3\cos(2(t - \dfrac{7\pi}{12})) + 4.\]

5. Точка\(P\) знаходиться на центральній лінії і тому горизонтальна відстань між\(P\) і\(Q\) становить одну чверть періоду. Таким чином, це горизонтальна відстань\(\dfrac{\pi}{4}\) і\(t\) -координата\(P\) є\[\dfrac{7\pi}{12} - \dfrac{\pi}{4} = \dfrac{4\pi}{12} = \dfrac{\pi}{3}.\]
Це може бути зсув фази для\(y = A\sin(B(t - C')) + D\). Отже, ще одне рівняння для цієї синусоїди\[y = 3\sin(2(t - \dfrac{\pi}{3})) + 4\]

Резюме

У цьому розділі ми вивчили наступні важливі поняття та ідеї: Для синусоїдальної функції виду\(f(t) = A\sin(B(t - C)) + D\) або\(f(t) = A\cos(B(t - C)) + D\) де\(A, B, C\), і\(D\) є дійсними числами з\(B > 0\):

• Значення\(|A|\) амплітуди синусоїдальної функції.
• Значення\(B\) визначає період синусоїдальної функції. період дорівнює\(2\pi\).
• Значення\(C\) - зсув фаз (горизонтальний зсув) синусоїдальної функції. Графік зміщується вправо if\(C > 0\) і зсувається вліво if\(C < 0\).
• Величина -\(D\) вертикальний зсув синусоїди. Горизонтальна лінія\(y = D\) - це так звана центральна лінія для графіка синусоїдальної функції.
• Важливі примітки про синусоїди на сторінці 103.