14: Рівняння Клаузіуса-Клапейрона

Перш ніж розпочати цю главу, ймовірно, було б непогано перечитати Розділи 9.2 та 9.3 Глави 9.

Рівняння Клаузіуса-Клапейрона пов'язує приховану теплоту (теплоту перетворення) випаровування або конденсації зі швидкістю зміни тиску пари з температурою. Або, у разі перетворення тверда рідина, вона пов'язує приховану теплоту плавлення або затвердіння зі швидкістю зміни температури плавлення тиском.

Уявімо пару в рівновазі зі своєю рідиною, що утримується в циліндрі поршнем, при постійній температурі - а саме температурі, при якій рідина і пара знаходяться в рівновазі - тобто точка кипіння (або конденсації) для цього тиску. Ми уявляємо поршень, який потрібно витягнути, при постійній температурі; рідина випаровується і тиск залишається постійним. Якщо поршень проштовхується, пари конденсуються, при постійній температурі і тиску. Під час цього процесу тиск і температура залишаються постійними, тому вільна енергія Гіббса системи постійна.

Нехай G ₁ - питома вільна енергія Гіббса для рідини

і G ₂ бути специфічною вільною енергією Гіббса для пари.

Припустимо, що маса dm рідини випаровується, так що вільна енергія Гіббса для рідини зменшується на G ₁ дм, а вільна енергія Гіббса для пари збільшується на G ₂ дм. Але вільна енергія Гіббса для системи постійна. Таким чином, це показує, що, коли ми маємо рідину в рівновазі зі своєю парою (тобто при температурі кипіння), конкретні вільні енергії Гіббса рідини та пари рівні. (Те ж саме справедливо, звичайно, і для молярних вільних енергій Гіббса.) Тобто:

\[H_{1}-T S_{1}=H_{2}-T S_{2}\]

або

\[ T\left(S_{2}-S_{1}\right)=H_{2}-H_{1},\]

в яких ентальпія і ентропія специфічні. Ліва сторона - питома прихована теплота випаровування, і ми вже знали з глави 9, що це дорівнює різниці в питомих ентальпіях рідини і пари.

Також можна записати рівність конкретних вільних енергій Гіббса рідини і пари.

\[U_{1}-T S_{1}+P V_{1}=U_{2}-T S_{2}+P V_{2},\]

або

\[T\left(S_{2}-S_{1}\right)=\left(U_{2}-U_{1}\right)+P\left(V_{2}-V_{1}\right).\]

Це показує, що прихована теплота випаровування переходить на дві речі: збільшити внутрішню енергію при випаровуванні (особливо збільшення потенційної енергії, коли молекули витягуються один від одного) і робота pDV, виконана проти зовнішнього тиску, коли обсяг збільшується. Таким чином, ми могли б розділити приховане тепло на внутрішнє приховане тепло і зовнішнє приховане тепло.

У вищесказаному ми уявляли, що якась рідина випаровується, коли ми вилучили поршень. Тепер уявімо, що ми змушуємо деяку рідину випаровуватися, коли ми додаємо трохи тепла при постійному обсязі. Питомі вільні енергії Гіббса рідини і пари збільшуються, але вони збільшуються на однакову кількість, тому що, як ми бачили, коли рідина і її пара знаходяться в рівновазі в точці кипіння, їх питомі вільні енергії Гіббса рівні. Таким чином

\[-S_{1} d T+V_{1} d P=-S_{2} d T+V_{2} d P,\]

або

\[\frac{d P}{d T}=\frac{S_{2}-S_{1}}{V_{2}-V_{1}}.\]

Ліва сторона - швидкість збільшення тиску пари з температурою, тоді як S ₂ − S ₁ дорівнює L/T, де L - питома прихована теплота випаровування. Таким чином, ми дійдемо до рівняння Клаузіуса-Клапейрона:

\[\frac{d P}{d T}=\frac{L}{T\left(V_{2}-V_{\mathrm{L}}\right)}.\]

Приклад: При 100 ^о С швидкість збільшення тиску пари пари становить 27,1 мм рт.ст. На градус Цельсія, а грам пари займає 1674 см ³. Яка питома прихована теплота пароутворення?

Відповідь:\(L=T\left(V_{2}-V_{1}\right) \frac{d P}{d T}\).

\( T=373.15 \mathrm{K} . \quad V_{2}-V_{1}=1.673 \mathrm{m}^{3} \mathrm{kg}^{-1}\).

\( \frac{d P}{d T}=1.36 \times 10^{4} \times 9.81 \times 2.71 \times 10^{-2}=3.616 \mathrm{PaK}^{-1}\).

Звідси

\( \underline{\underline{L=2.26 \times 10^{6} \mathrm{J} \mathrm{kg}^{-1}}}\).

Цей же аргумент можна використовувати для зв'язку швидкості зміни температури плавлення з тиском твердого тіла з його прихованою теплотою плавлення. Рівняння Клаузіуса-Клапейрона тоді набуває вигляду

\[\frac{d T}{d P}=\frac{T\left(V_{2}-V_{1}\right)}{L}.\]

Для більшості речовин питомий обсяг рідини (V ₂) більше питомого обсягу твердої речовини (V ₁); але для H ₂ O, Bi і Ga, V ₂ < V ₁ і dT/dP негативний.

Приклад: Для системи крижаної води

\( \begin{array}{l}{L=3.36 \times 10^{5} \mathrm{J} \mathrm{kg}^{-1}} \\ {V_{2}=10^{-3} \mathrm{m}^{3} \mathrm{kg}^{-1}} \\ {V_{1}=1.091 \times 10^{-3} \mathrm{m}^{3} \mathrm{kg}^{-1}} \\ {T=273.15 \mathrm{K}} \end{array}\)

Звідси

\( \frac{d T}{d P}=-7.4 \times 10^{-8} \mathrm{KPa}^{-1}\)

Це приблизно −7,4 × 10 ⁻³ кельвінів на атмосферу

Тверді речовини, рідини, гази, ентропія та функція Гіббса.

З трьох фаз, тверда, рідка і пара, тверда є найбільш впорядкованою (має найменшу ентропію), а пар - найбільш невпорядкованим (має найбільшу ентропію). Тепер рівняння 12.6.12a говорить нам, що (G /T) = −S Це означає, що при заданому тиску функція пари Гіббса швидко зменшується зі збільшенням температури, тоді як функція Гіббса твердого тіла зменшується відносно повільно. Схематично функція Гіббса трьох фаз для Н ₂ О при атмосферному тиску виглядає приблизно так:

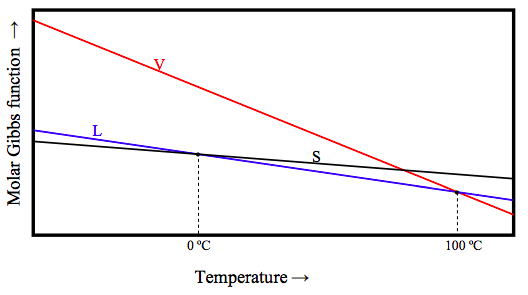
Нижче 0 ºC функція Гіббса найнижча для твердого тіла, і це стабільна фаза. Між 0 ºC і 100 ºC функція Гіббса є найнижчою для рідини, і це стабільна фаза. Вище 100 ºC функція Гіббса найнижча для пари, і це стабільна фаза. При 0 ºC молярна функція Гіббса твердої та рідкої рідини рівні; дві фази знаходяться в рівновазі. При 100 ºC молярна функція Гіббса газу і рідини рівні; дві фази знаходяться в рівновазі.

Нахили і перехоплення цих ліній змінюються не тільки від речовини до речовини, але і, для даної речовини, тиском. Відношення Максвелла 12.6.16 говорить нам\( \left(\frac{\partial S}{\partial P}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{P}\), що спосіб зміни ентропії з тиском пов'язаний з коефіцієнтом розширення. Для більшості речовин (вода від 0 ºC до 4 ºC є винятком) коефіцієнт розширення позитивний, тому це говорить нам про те, що ентропія зменшується зі збільшенням тиску, і збільшується зі зменшенням тиску. Зміна ентропії з тиском найбільше для пари, так що при менших тисках нахил парової лінії на графіку функції Гіббса з температурою буде набагато крутіше, а ситуація буде виглядати наступним чином:

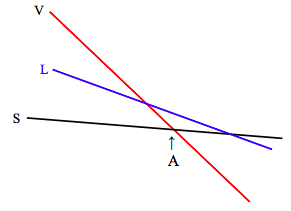
При температурах нижче А функція Гіббса найнижча для твердого тіла, і це стабільна фаза. При температурі вище А функція Гіббса найнижча для пари, і це стабільна фаза. При тиску, представленому на наведеній вище діаграмі, рідина ніколи не є стабільною фазою. Речовина сублімується від твердого до пари при підвищенні температури.

При тиску, відповідному лінії потрійної точки (нагадайте про себе, подивившись на цифри VI.3, VI.4 і VI.8), діаграма виглядає так:

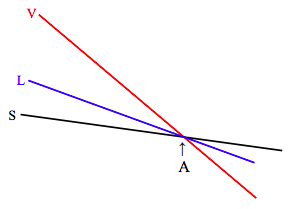
У потрійній точці (А) молярні функції Гіббса всіх трьох фаз рівні, і всі три фази знаходяться в рівновазі. Коли ви збільшуєте температуру від нижче А до вище А, речовина сублімується безпосередньо від твердого до пари, як це також видно з малюнка VI.5.