23.4: Рівняння Клаузіуса-Клапейрона

Випаровування

У розділі 23.3 було отримано рівняння Клапейрона для точок плавлення.

$$\dfrac{dP}{dT} = \dfrac{ΔH_{molar}}{TΔV_{molar}} \nonumber$$

Однак наш аргумент насправді є досить загальним і повинен триматися за рівноваги пари, а також. Єдина проблема полягає в тому, що молярний об'єм газів аж ніяк не так добре постійний, як для конденсованих фаз. (Тобто, для фаз конденсату обидві$α$ і$κ$ досить малі).

Ми можемо написати:

$$\dfrac{dP}{dT} =\dfrac{ ΔH_{molar}}{TΔV_{molar}} = \dfrac{ΔH_{molar}}{T} \left[V_{molar}^{gas}-V_{molar}^{liquid} \right] \nonumber$$

як

$$V_{molar}^{gas} \gg V_{molar}^{liquid} \nonumber$$

ми можемо наблизити

$$V_{molar}^{gas}-V_{molar}^{liquid} \nonumber$$

просто взявши$V_{molar}^{gas}$. Далі більше якщо пар вважається ідеальним газом, то

$$V_{molar}^{gas} = \dfrac{RT}{P} \nonumber$$

Ми отримуємо

$$\dfrac{1}{P} .\dfrac{dP}{dT} = \dfrac{d \ln P}{dT} = \dfrac{ΔH_{molar}^{vap}}{RT^2} \label{CCe}$$

$\ref{CCe}$Рівняння відоме як рівняння Клаузіуса-Клапейрона. Ми можемо додатково опрацювати нашу інтеграцію та знайти, як змінюється рівноважний тиск пари з температурою:

$$\ln \left( \dfrac{P_2}{P_1} \right)= \dfrac{-ΔH_{molar}^{vap}}{R} \left[\dfrac{1}{T_2}-\dfrac{1}{T_1} \right] \nonumber$$

Таким чином, якщо ми знаємо молярну ентальпію випаровування, ми можемо передбачити парові лінії на діаграмі. Звичайно, зроблені наближення, ймовірно, призведуть до відхилень, якщо пара не ідеальна або дуже щільна (наприклад, наближається до критичної точки).

Рівняння Клапейрона

Клапейрон намагається відповісти на питання про те, яка форма лінії двофазного співіснування. У$P-T$ площині ми бачимо функцію$P(T)$, яка дає нам залежність від$T$ вздовж кривої співіснування.$P$

Розглянемо дві фази, позначаються$\alpha$ і$\beta$, знаходяться в рівновазі один з одним. Це можуть бути тверді та рідкі, рідкі та газові, тверді та газові, дві тверді фази тощо. $\mu_\alpha (P, T)$$\mu_\beta (P, T)$Дозволяти і бути хімічними потенціалами двох фаз. Ми щойно побачили, що

$$\mu_\alpha (P, T) = \mu_\beta (P, T) \label{14.1}$$

Далі припустимо, що тиск і температура змінюються на$dP$ і$dT$. Зміни хімічних потенціалів кожної фази

$$d \mu_{\alpha} (P, T) = d \mu_{\beta} (P, T) \label{14.2a}$$

$$\left( \dfrac{\partial \mu_{\alpha}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\alpha}}{\partial T} \right)_P dT = \left( \dfrac{\partial \mu_{\beta}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\beta}}{\partial T} \right)_P dT \label{14.2b}$$

Однак$G(n, P, T) = n \mu (P, T)$, оскільки молярна вільна енергія$\bar{G} (P, T)$, яка є$G(n, P, T)/n$, також якраз дорівнює хімічному потенціалу

$$\bar{G} (P, T) = \dfrac{G(n, P, T)}{n} = \mu (P, T) \label{14.3}$$

Більш того,$\bar{G}$ похідні від

$$\left( \dfrac{\partial \bar{G}}{\partial P} \right)_T = \bar{V}, \: \: \: \: \: \: \: \left( \dfrac{\partial \bar{G}}{\partial T} \right)_P = -\bar{S} \label{14.4}$$

Застосовуючи ці результати до умови хімічного потенціалу в$\ref{14.2b}$ рівнянні, отримано

\ [\ почати {вирівняти}\ ліворуч (\ dfrac {\ частковий\ бар {G} _\ альфа} {\ частковий P}\ праворуч) _T дП +\ ліворуч (\ dfrac {\ частковий\ бар {G} _\ альфа} {\ частковий T}\ правий) _P dT &=\ лівий (\ dfrac {\ частковий\ бар {G} _\ бета} {\ частковий T}\ правий) _P &=\ лівий (\ dfrac {\ частковий\ бар {G} _\ бета} {\ частковий T}\\ праворуч) _T дП +\ ліворуч (\ dfrac {\ частковий\ бар {G} _\ бета} {\ частковий T}\ правий) _P dT\

$$5pt] \bar{V}_\alpha dP - \bar{S}_\alpha dT &= \bar{V}_\beta dP - \bar{S}_\beta dT \end{align} \label{14.5}$$

Розділивши наскрізь на$dT$, отримуємо

\ [\ почати {вирівнювання}\ бар {V} _\ альфа\ dfrac {\ частковий P} {\ частковий T} -\ бар {S} _\ альфа &=\ бар {V} _\ бета\ dfrac {\ частковий P} {\ частковий T} -\ бар {S} _\ бета\

\ [5pt] (\ бар {V} _\ альфа -\ бар {V} _\ бета)\ dfrac {\ частковий P} {\ частковий T} &=\ бар {S} _\ альфа -\ бар {S} _\ бета\

$$5pt] \dfrac{dP}{dT} &= \dfrac{\bar{S}_\alpha - \bar{S}_\beta}{\bar{V}_\alpha - \bar{V}_\beta} \end{align} \label{14.6}$$

Важливість величини$dP/dT$ полягає в тому, що вона представляє нахил кривої співіснування на фазовій діаграмі між двома фазами. Тепер, в рівновазі$dG = 0$, і з тих пір$G = H - TS$, випливає, що$dH = T \: dS$ при фіксованому$T$. У вузькому діапазоні температур, в якому дві фази знаходяться в рівновазі, можна припустити,$H$ що не залежить від$T$, отже, ми можемо писати$S = H/T$. Отже, ми можемо записати різницю молярної ентропії як

$$\bar{S}_\alpha - \bar{S}_\beta = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T} \label{14.7}$$

і похідна тиску$dP/dT$ стає

$$\dfrac{dP}{dT} = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T (\bar{V}_\alpha - \bar{V}_\beta)} = \dfrac{\Delta_{\alpha \beta} \bar{H}}{T \Delta_{\alpha \beta} \bar{V}} \label{14.8}$$

результат, відомий як рівняння Клапейрона, який говорить нам, що нахил кривої співіснування пов'язаний зі співвідношенням молярної ентальпії між фазами до зміни молярного об'єму між фазами. Якщо фазова рівновага знаходиться між твердою і рідкою фазами, то$\Delta_{\alpha \beta} \bar{H}$ і$\Delta_{\alpha \beta} \bar{V}$ є$\Delta \bar{H}_\text{fus}$ і$\Delta \bar{V}_\text{fus}$, відповідно. Якщо фазова рівновага знаходиться між рідкою і газовою фазами, то$\Delta_{\alpha \beta} \bar{H}$ і$\Delta_{\alpha \beta} \bar{V}$ є$\Delta \bar{H}_\text{vap}$ і$\Delta \bar{V}_\text{vap}$, відповідно.

Для рівноваги рідина-газ можна зробити деякі цікаві наближення при використанні рівняння Клапейрона. Для цієї рівноваги рівняння$\ref{14.8}$ стає

$$\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}_\text{vap}}{T (\bar{V}_g - \bar{V}_l)} \label{14.9}$$

У цьому випадку$\bar{V}_g \gg \bar{V}_l$, і ми можемо наблизити Рівняння$\ref{14.9}$ як

$$\dfrac{dP}{dT} \approx \dfrac{\Delta \bar{H}_\text{vap}}{T \bar{V}_g} \label{14.10}$$

Припустимо, що ми можемо розглядати парову фазу як до ідеального газу. Звичайно, це не гарне наближення, настільки близьке до точки випаровування, але це призводить до прикладу, який ми можемо інтегрувати. З тих пір$PV_g = nRT$$P \bar{V}_g = RT$, Рівняння$\ref{14.10}$ стає

\ [\ почати {вирівняти}\ dfrac {dP} {dT} &=\ dfrac {\ Дельта\ бар {H} _\ текст {вап} P} {RT^2}\

\ [5pt]\ dfrac {1} {P}\ dfrac {dP} {dT} &=\ dfrac {\ дельта\ бар {H} _\ текст {вап}} {RT^2}\

$$5pt] \dfrac{d \: \text{ln} \: P}{dT} &= \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} \end{align} \label{14.11}$$

який називається рівнянням Клаузіуса-Клапейрона. Тепер ми інтегруємо обидві сторони, що дає

$$\text{ln} \: P = -\dfrac{\Delta \bar{H}_\text{vap}}{RT} + C$$

де$C$ константа інтеграції. Збільшивши обидві сторони, знаходимо

$$P(T) = C' e^{-\Delta \bar{H}_\text{vap}/RT}$$

який насправді має неправильну кривизну для великих$T$, але оскільки лінія співіснування рідина-пара закінчується у критичній точці, поки$T$ не надто велика, наближення, що призводить до вищевказаного виразу, не таке вже й погане.

Якщо ми, замість цього, інтегрувати обидві сторони, зліва від$P_1$ до$P_2$, а справа від$T_1$ до$T_2$, ми знаходимо

\ [\ почати {вирівняти}\ int_ {P_1} ^ {P_2} d\:\ текст {ln}\: P &=\ int_ {T_1} ^ {T_2}\ dfrac {\ Дельта\ бар {H} _\ текст {вап}} {RT^2} dT\

\ [5pt]\ текст {ln}\:\ лівий (\ dfrac {P_2} {P_1}\ праворуч) &= -\ dfrac {\ дельта\ бар {H} _\ текст {vap}} {R}\ ліворуч (\ dfrac {1} {T_2} -\ dfrac {1} {T_1}\ праворуч)\

$$5pt] &= \dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{T_1 - T_1}{T_1 T_2} \right) \end{align} \label{14.12}$$

припускаючи, що$\Delta \bar{H}_\text{vap}$ це не залежить від$T$. Тут$P_1$ знаходиться тиск рідкої фази, а$P_2$ це тиск парової фази. Припустимо, ми знаємо$P_2$ температуру$T_2$, і хочемо знати$P_3$ при іншій температурі$T_3$. Вищевказаний результат можна записати як

$$\text{ln} \: \left( \dfrac{P_3}{P_1} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_3} - \dfrac{1}{T_1} \right) \label{14.13}$$

Віднімаючи два результату, отримаємо

$$\text{ln} \: \left( \dfrac{P_2}{P_3} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_3} \right) \label{14.14}$$

так що ми можемо визначити тиск пари при будь-якій температурі, якщо вона відома як одна температура.

Для того, щоб проілюструвати використання цього результату, розглянемо наступний приклад:

Приклад$\PageIndex{1}$

При$1 \: \text{bar}$, температура кипіння води дорівнює$373 \: \text{K}$. При якому тиску кипить вода$473 \: \text{K}$? Приймати тепло випаровування води слід$40.65 \: \text{kJ/mol}$.

Рішення

Нехай$P_1 = 1 \: \text{bar}$ і$T_1 = 373 \: \text{K}$. Беремо$T_2 = 473 \: \text{K}$, і нам потрібно порахувати$P_2$. Підставляючи в цифри, знаходимо

\ [\ почати {вирівняти}\ текст {ln}\: P_2 (\ текст {бар}) &= -\ dfrac {(40.65\:\ текст {кДж/моль}) (1000\:\ текст {Дж/кДж})} {8.3145\:\ текст {J/моль}\ cdot\ текст {K}}\ лівий (\ dfrac {1} {473\:\ текст {K}} -\ dfrac {1} {373\:\ текст {K}}\ праворуч) = 2.77\

$$5pt] P_2(\text{bar}) &= (1 \: \text{bar}) \: e^{2.77} = 16 \: \text{bar} \end{align}$$

Рівняння Клапейрона

Клапейрон намагається відповісти на питання про те, яка форма лінії двофазного співіснування. У$P-T$ площині ми бачимо функцію$P(T)$, яка дає нам залежність від$T$ вздовж кривої співіснування.$P$

Розглянемо дві фази, позначаються$\alpha$ і$\beta$, знаходяться в рівновазі один з одним. Це можуть бути тверді та рідкі, рідкі та газові, тверді та газові, дві тверді фази тощо. $\mu_\alpha (P, T)$$\mu_\beta (P, T)$Дозволяти і бути хімічними потенціалами двох фаз. Ми щойно побачили, що

$$\mu_\alpha (P, T) = \mu_\beta (P, T) \label{14.1}$$

Далі припустимо, що тиск і температура змінюються на$dP$ і$dT$. Зміни хімічних потенціалів кожної фази

$$d \mu_{\alpha} (P, T) = d \mu_{\beta} (P, T) \label{14.2a}$$

$$\left( \dfrac{\partial \mu_{\alpha}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\alpha}}{\partial T} \right)_P dT = \left( \dfrac{\partial \mu_{\beta}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\beta}}{\partial T} \right)_P dT \label{14.2b}$$

Однак$G(n, P, T) = n \mu (P, T)$, оскільки молярна вільна енергія$\bar{G} (P, T)$, яка є$G(n, P, T)/n$, також якраз дорівнює хімічному потенціалу

$$\bar{G} (P, T) = \dfrac{G(n, P, T)}{n} = \mu (P, T) \label{14.3}$$

Більш того,$\bar{G}$ похідні від

$$\left( \dfrac{\partial \bar{G}}{\partial P} \right)_T = \bar{V}, \: \: \: \: \: \: \: \left( \dfrac{\partial \bar{G}}{\partial T} \right)_P = -\bar{S} \label{14.4}$$

Застосовуючи ці результати до умови хімічного потенціалу в$\ref{14.2b}$ рівнянні, отримано

$$\begin{align} \left( \dfrac{\partial \bar{G}_\alpha}{\partial P} \right)_T dP + \left( \dfrac{\partial \bar{G}_\alpha}{\partial T} \right)_P dT &= \left( \dfrac{\partial \bar{G}_\beta}{\partial P} \right)_T dP + \left( \dfrac{\partial \bar{G}_\beta}{\partial T} \right)_P dT \\[5pt] \bar{V}_\alpha dP - \bar{S}_\alpha dT &= \bar{V}_\beta dP - \bar{S}_\beta dT \end{align} \label{14.5}$$

Розділивши наскрізь на$dT$, отримуємо

$$\begin{align} \bar{V}_\alpha \dfrac{\partial P}{\partial T} - \bar{S}_\alpha &= \bar{V}_\beta \dfrac{\partial P}{\partial T} - \bar{S}_\beta \\[5pt] (\bar{V}_\alpha - \bar{V}_\beta) \dfrac{\partial P}{\partial T} &= \bar{S}_\alpha - \bar{S}_\beta \\[5pt] \dfrac{dP}{dT} &= \dfrac{\bar{S}_\alpha - \bar{S}_\beta}{\bar{V}_\alpha - \bar{V}_\beta} \end{align} \label{14.6}$$

Важливість величини$dP/dT$ полягає в тому, що вона представляє нахил кривої співіснування на фазовій діаграмі між двома фазами. Тепер, в рівновазі$dG = 0$, і з тих пір$G = H - TS$, випливає, що$dH = T \: dS$ при фіксованому$T$. У вузькому діапазоні температур, в якому дві фази знаходяться в рівновазі, можна припустити,$H$ що не залежить від$T$, отже, ми можемо писати$S = H/T$. Отже, ми можемо записати різницю молярної ентропії як

$$\bar{S}_\alpha - \bar{S}_\beta = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T} \label{14.7}$$

і похідна тиску$dP/dT$ стає

$$\dfrac{dP}{dT} = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T (\bar{V}_\alpha - \bar{V}_\beta)} = \dfrac{\Delta_{\alpha \beta} \bar{H}}{T \Delta_{\alpha \beta} \bar{V}} \label{14.8}$$

результат, відомий як рівняння Клапейрона, який говорить нам, що нахил кривої співіснування пов'язаний зі співвідношенням молярної ентальпії між фазами до зміни молярного об'єму між фазами. Якщо фазова рівновага знаходиться між твердою і рідкою фазами, то$\Delta_{\alpha \beta} \bar{H}$ і$\Delta_{\alpha \beta} \bar{V}$ є$\Delta \bar{H}_\text{fus}$ і$\Delta \bar{V}_\text{fus}$, відповідно. Якщо фазова рівновага знаходиться між рідкою і газовою фазами, то$\Delta_{\alpha \beta} \bar{H}$ і$\Delta_{\alpha \beta} \bar{V}$ є$\Delta \bar{H}_\text{vap}$ і$\Delta \bar{V}_\text{vap}$, відповідно.

Для рівноваги рідина-газ можна зробити деякі цікаві наближення при використанні рівняння Клапейрона. Для цієї рівноваги рівняння$\ref{14.8}$ стає

$$\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}_\text{vap}}{T (\bar{V}_g - \bar{V}_l)} \label{14.9}$$

У цьому випадку$\bar{V}_g \gg \bar{V}_l$, і ми можемо наблизити Рівняння$\ref{14.9}$ як

$$\dfrac{dP}{dT} \approx \dfrac{\Delta \bar{H}_\text{vap}}{T \bar{V}_g} \label{14.10}$$

Припустимо, що ми можемо розглядати парову фазу як до ідеального газу. Звичайно, це не гарне наближення, настільки близьке до точки випаровування, але це призводить до прикладу, який ми можемо інтегрувати. З тих пір$PV_g = nRT$$P \bar{V}_g = RT$, Рівняння$\ref{14.10}$ стає

$$\begin{align} \dfrac{dP}{dT} &= \dfrac{\Delta \bar{H}_\text{vap} P}{RT^2} \\[5pt] \dfrac{1}{P} \dfrac{dP}{dT} &= \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} \\[5pt] \dfrac{d \: \text{ln} \: P}{dT} &= \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} \end{align} \label{14.11}$$

який називається рівнянням Клаузіуса-Клапейрона. Тепер ми інтегруємо обидві сторони, що дає

$$\text{ln} \: P = -\dfrac{\Delta \bar{H}_\text{vap}}{RT} + C \nonumber$$

де$C$ константа інтеграції. Збільшивши обидві сторони, знаходимо

$$P(T) = C' e^{-\Delta \bar{H}_\text{vap}/RT} \nonumber$$

який насправді має неправильну кривизну для великих$T$, але оскільки лінія співіснування рідина-пара закінчується у критичній точці, поки$T$ не надто велика, наближення, що призводить до вищевказаного виразу, не таке вже й погане.

Якщо ми, замість цього, інтегрувати обидві сторони, зліва від$P_1$ до$P_2$, а справа від$T_1$ до$T_2$, ми знаходимо

$$\begin{align} \int_{P_1}^{P_2} d \: \text{ln} \: P &= \int_{T_1}^{T_2} \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} dT \\[5pt] \text{ln} \: \left( \dfrac{P_2}{P_1} \right) &= -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_1} \right) \\[5pt] &= \dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{T_1 - T_1}{T_1 T_2} \right) \end{align} \label{14.12}$$

припускаючи, що$\Delta \bar{H}_\text{vap}$ це не залежить від$T$. Тут$P_1$ знаходиться тиск рідкої фази, а$P_2$ це тиск парової фази. Припустимо, ми знаємо$P_2$ температуру$T_2$, і хочемо знати$P_3$ при іншій температурі$T_3$. Вищевказаний результат можна записати як

$$\text{ln} \: \left( \dfrac{P_3}{P_1} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_3} - \dfrac{1}{T_1} \right) \label{14.13}$$

Віднімаючи два результату, отримаємо

$$\text{ln} \: \left( \dfrac{P_2}{P_3} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_3} \right) \label{14.14}$$

так що ми можемо визначити тиск пари при будь-якій температурі, якщо вона відома як одна температура.

Для того, щоб проілюструвати використання цього результату, розглянемо наступний приклад:

ПрикладTemplate:Index

При$1 \: \text{bar}$, температура кипіння води дорівнює$373 \: \text{K}$. При якому тиску кипить вода$473 \: \text{K}$? Приймати тепло випаровування води слід$40.65 \: \text{kJ/mol}$.

Рішення

Нехай$P_1 = 1 \: \text{bar}$ і$T_1 = 373 \: \text{K}$. Беремо$T_2 = 473 \: \text{K}$, і нам потрібно порахувати$P_2$. Підставляючи в цифри, знаходимо

$$\begin{align} \text{ln} \: P_2(\text{bar}) &= -\dfrac{(40.65 \: \text{kJ/mol})(1000 \: \text{J/kJ})}{8.3145 \: \text{J/mol} \cdot \text{K}} \left( \dfrac{1}{473 \: \text{K}} - \dfrac{1}{373 \: \text{K}} \right) = 2.77 \\[5pt] P_2(\text{bar}) &= (1 \: \text{bar}) \: e^{2.77} = 16 \: \text{bar} \end{align} \nonumber$$

Цілі навчання

• Застосовуйте рівняння Клаузіуса-Клапейрона для оцінки тиску пари при будь-якій температурі.
• Оцініть теплоту фазового переходу від тиску пари, виміряного при двох температурах.

Крива випаровування s більшості рідин має подібні форми з тиском пари неухильно зростає з підвищенням температури (рис.$\PageIndex{1}$).

$\PageIndex{1}$:Рисунок Тиск пари декількох рідин як функція температури. Точка, в якій крива тиску пари перетинає лінію Р = 1 атм (пунктирна), є нормальною температурою кипіння рідини. (CC BY-SA-NC; Анонімний)

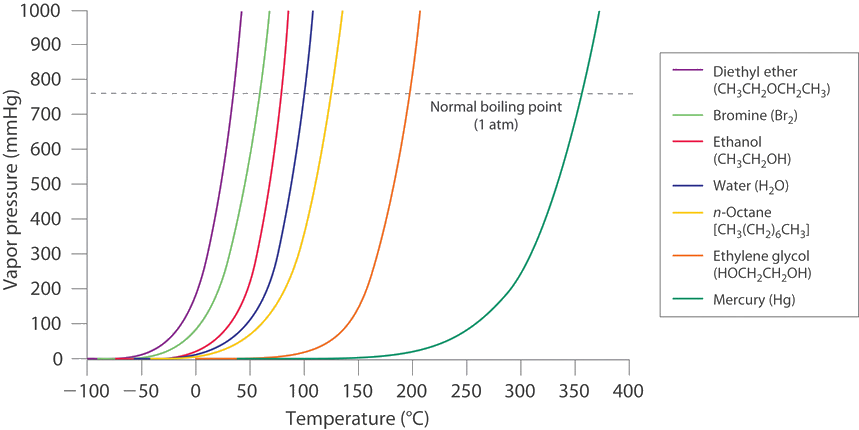
Хорошим підходом є пошук математичної моделі підвищення тиску в залежності від температури. Експерименти показали, що тиск пари$P$ і температура$T$ пов'язані,

$$P \propto \exp \left(- \dfrac{\Delta H_{vap}}{RT}\right) \ \label{1}$$

де$\Delta{H_{vap}}$ - ентальпія (теплота) пароутворення і$R$ є газовою постійною (8,3145 Дж моль ^-1 К ^-1).

Просте співвідношення можна знайти шляхом інтеграції Equation\ ref {1} між двома кінцевими точками тиску і температури:

$$\ln \left( \dfrac{P_1}{P_2} \right) = \dfrac{\Delta H_{vap}}{R} \left( \dfrac{1}{T_2}- \dfrac{1}{T_1} \right) \label{2}$$

де$P_1$ і$P_2$ знаходяться тиск пари при двох температурах$T_1$ і$T_2$. Рівняння\ ref {2} відоме як рівняння Клаузіуса-Клапейрона і дозволяє оцінити тиск пари при іншій температурі, якщо тиск пари відомий при певній температурі, і якщо відома ентальпія випаровування.

Альтернативна рецептура

Порядок температур у рівнянні\ ref {2} має значення, оскільки рівняння Клаузіуса-Клапейрона іноді записується з від'ємним знаком (і зміненим порядком температур):

$$\ln \left( \dfrac{P_1}{P_2} \right) = - \dfrac{\Delta H_{vap}}{R} \left( \dfrac{1}{T_1}- \dfrac{1}{T_2} \right) \label{2B}$$

Приклад$\PageIndex{1}$: Vapor Pressure of Water

Тиск пари води становить 1,0 атм при 373 К, а ентальпія пароутворення - 40,7 кДж моль ^-1. Оцініть тиск пари при температурі 363 і 383 К відповідно.

Рішення

Використовуючи рівняння Клаузіуса-Клапейрона (Рівняння$\ref{2B}$), ми маємо:

$$\begin{align} P_{363} &= 1.0 \exp \left[- \left(\dfrac{40,700}{8.3145}\right) \left(\dfrac{1}{363\;K} -\dfrac{1}{373\; K}\right) \right] \nonumber \\[4pt] &= 0.697\; atm \nonumber \end{align} \nonumber$$

$$\begin{align} P_{383} &= 1.0 \exp \left[- \left( \dfrac{40,700}{8.3145} \right)\left(\dfrac{1}{383\;K} - \dfrac{1}{373\;K} \right) \right] \nonumber \\[4pt] &= 1.409\; atm \nonumber \end{align} \nonumber$$

Відзначимо, що підвищення тиску пари з 363 К до 373 К становить 0,303 атм, а ось приріст з 373 до 383 К дорівнює 0,409 атм. Збільшення тиску пари не є лінійним процесом.

Обговорення

Ми можемо використовувати рівняння Клаузіуса-Клапейрона для побудови всієї кривої вапоризації. Існує відхилення від експериментального значення, тобто тому, що ентальпія випаровування трохи змінюється в залежності від температури.

Рівняння Клаузіуса-Клапейрона також може бути застосовано до сублімації; наступний приклад показує його застосування при оцінці теплоти сублімації.

Приклад$\PageIndex{2}$: Sublimation of Ice

Тиск пари льоду при 268 К і 273 К складають 2,965 і 4,560 торр відповідно. Оцініть теплоту сублімації льоду.

Рішення

Ентальпія сублімації є$\Delta{H}_{sub}$. Використовуйте аркуш паперу і виведіть рівняння Клаузіуса-Клапейрона, щоб ви могли отримати вигляд:

$$\begin{align} \Delta H_{sub} &= \dfrac{ R \ln \left(\dfrac{P_{273}}{P_{268}}\right)}{\dfrac{1}{268 \;K} - \dfrac{1}{273\;K}} \nonumber \\[4pt] &= \dfrac{8.3145 \ln \left(\dfrac{4.560}{2.965} \right)}{ \dfrac{1}{268\;K} - \dfrac{1}{273\;K} } \nonumber \\[4pt] &= 52,370\; J\; mol^{-1}\nonumber \end{align} \nonumber$$

Відзначимо, що теплота сублімації - це сума теплоти плавлення (6,006 Дж/моль при 0° C і 101 кПа) і теплоти випаровування (45 051 Дж/моль при 0° C).

9 лют 2018 р. 11:53

http://www.kayelaby.npl.co.uk/chemis...3_4/3_4_1.html

Вправа$\PageIndex{2}$

Покажіть, що тиск пари льоду при 274 К вище, ніж у води при тій же температурі. Зверніть увагу, що крива пароутворення також називається кривою випаровування.

Приклад$\PageIndex{3}$: Vaporization of Ethanol

Розрахуйте$\Delta{H_{vap}}$ для етанолу, враховуючи тиск пари при 40 ^о С = 150 торр. Нормальна температура кипіння для етанолу становить 78 ^o С.

Рішення

Визнайте, що у нас є ДВА набори$(P,T)$ даних:

• Набір 1: (150 торр при 40+273K)
• Набір 2: (760 торр при 78+273K)

Потім ми безпосередньо використовуємо ці дані в Equation\ ref {2B}

$$\begin{align*} \ln \left(\dfrac{150}{760} \right) &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ \dfrac{1}{313} - \dfrac{1}{351}\right] \\[4pt] \ln 150 -\ln 760 &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ \dfrac{1}{313} - \dfrac{1}{351}\right] \\[4pt] -1.623 &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ 0.0032 - 0.0028 \right] \end{align*}$$

Тоді рішення для$\Delta{H_{vap}}$

$$\begin{align*} \Delta{H_{vap}} &= 3.90 \times 10^4 \text{ joule/mole} \\[4pt] &= 39.0 \text{ kJ/mole} \end{align*}$$

Розширена примітка

Важливо не використовувати рівняння Клаузіуса-Клапейрона для переходу твердого тіла до рідини. Це вимагає використання більш загального рівняння Клапейрона.

$$\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}}{T \Delta \bar{V}} \nonumber$$

де$\Delta \bar{H}$ і$\Delta \bar{V}$ - молярна зміна ентальпії (ентальпія злиття в даному випадку) і об'єму відповідно між двома фазами в переході.