1.7: Безперервність

Безперервність

Безперервність - важливе поняття в теорії реальних функцій. Безперервна функція - це та, вихід якої$f(x)$ не зазнає різких стрибків при$x$ зміні на крихітні суми. Функція може бути безперервною над усім доменом або лише підмножиною свого домену. Наприклад,$\sin(x)$ є безперервним для всіх$x$, тоді як$f(x) = 1/x$ є переривчастим при$x = 0$. Ще одна функція, яка є переривчастою в$x=0$ є ступінчаста функція $$\Theta(x) = \left\{\begin{array}{ll} 1, &\;\;\;\textrm{for} \; x \ge 0\\ 0,&\;\;\; \textrm{otherwise.}\end{array}\right.$$ Математики навіть придумали функції, які перериваються скрізь у своїй області, але ми не будемо мати справу з такими випадками.

Суворе визначення наступності полягає в наступному:

Визначення: Слово

Функція$f$ є безперервною в точці,$x_0$ якщо для будь-якого$\epsilon >0$, ми можемо знайти$\delta >0$ таку, що установка$x$ ближче,$x_0$ ніж відстань$\delta$$f(x)$ наближає до$f(x_0)$ зазначеної відстані$\epsilon$.

Це дуже складне речення, і його може бути простіше зрозуміти, використовуючи цю ілюстрацію:

Малюнок$\PageIndex{1}$

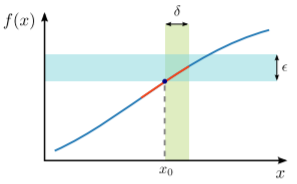
Контрприклад, з функцією, яка має розрив у деяких$x_0$, показаний нижче:

Малюнок$\PageIndex{2}$

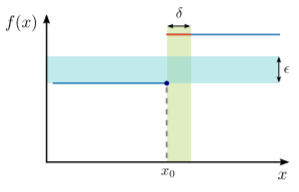
Якщо ми виберемо$\epsilon$ менше, ніж розрив, то незалежно від того, яке значення$\delta > 0$ ми намагаємося, будь-який вибір$0 < x < \delta$ дасть значення$f(x)$, що далі, ніж$\epsilon$ від$f(x_0)$. Отже, умова безперервності порушується для досить малих варіантів$\epsilon = 1/2$, і ми говоримо, що$f$ є переривчастим в$x_0$.