22.7: Додаток А
- Page ID
- 76147
Різні проблеми
У цьому додатку я пропоную ряд випадкових задач в класичній механіці. Вони не в якомусь певному порядку - вони приходять так само, як я думаю про них, і вони не обов'язково пов'язані з жодною з тем, що обговорюються в будь-якому з розділів. Вони призначені лише для того, щоб зайняти вас у ті похмурі, дощові дні, коли вам нічого кращого робити. Рішення будуть у Додатку B - за винятком того, що всякий раз, коли я додаю будь-які нові проблеми до Додатка А, які я час від часу буду чекати кілька днів, перш ніж публікувати рішення в Додатку B.
_____________________
Жодна книга з класичної механіки не обходиться без проблеми драбини, що спирається на стіну. Ось, отже, проблема сходів - за винятком того, що вона не має нічого спільного з механікою, і її ставлять тут просто заради задоволення. Це проблема лише в геометрії, але це та, яку деякі люди спочатку вважають важкою. Навіть здається важким спробувати знайти приблизне рішення, намагаючись намалювати його точно до масштабу, і я навмисно не намалював його в масштабі, тому ви не можете знайти відповідь, просто взявши лінійку і вимірявши її!
Дві сходи, довжиною 8 м і 10 м, спираються на дві стіни, як показано на малюнку. Їх точка перетину знаходиться на 3 м над землею. Яке відстань між стінами?
Маятник довжини\( l_{0}\), приводиться в рух так, що він описує конус, як показано напіввертикального кута\( \alpha\), боб описує горизонтальне коло з кутовою швидкістю\( \Omega\)
Покажіть, що
\( \cos\alpha=\frac{\text{g}}{l_{0}\Omega^{2}}\).
Це, звичайно, дуже банальна проблема, не гідна вашої хитрості. Вона дається лише як вступ до наступної проблеми.
Струна маятника проходить через дошку, як показано на малюнку нижче, таким чином, що, опускаючи або піднімаючи дошку, довжина струни під дошкою може варіюватися. Частина під дошкою спочатку має довжину\( l_{0}\), і вона приводиться в рух як конічний маятник, так що кутова швидкість і напіввертикальний кут пов'язані
\( \cos\ \alpha=\frac{\text{g}}{l_{0}\Omega^{2}}\).
Оскільки дошка піднімається або опускається (або, як варіант, маятник опускається або піднімається), і, отже, довжина\( l\) below the board is varied, the semivertical angle \( \theta\) зміниться, і кутова швидкість\( \omega\). (Символи\( l_{0}\), \( \alpha\) і\( \Omega\) представляють початкові значення цих величин.)
Покажіть, що
- \( l^{3}\sin^{3}\theta\tan\theta\) is constant,
- \( \omega^{3}\cot^{2}\theta\) is constant,
- \( \omega^{3}(\omega l^{2}\ -\ \Omega l_{0}^{2}\sin^{2}\alpha)\) is constant.
Start with the following initial conditions:
\( l_{0}\ =\ 50\ \text{cm} \qquad \Omega\ =\ 5\ \text{rad s}^{-1}\)
and assume that \( \text{g}\ =\ 9.8\ \text{m s}^{=2}\), so that \( \alpha\ =\ 38^{\circ}\ 22^{\prime}\).
- Plot a graph of \( \theta\) (vertically) versus \( l\) (horizontally), for \( l\ =\ 0\) to 1 m. When \( l\) = 40 cm, what is \( \theta\) correct to one arcmin?
- Plot a graph of \( \omega\) (vertically) versus \( \theta\) (horizontally), for \( \theta\) = 0 to 70o.
- Plot a graph of \( \omega\) (vertically) versus \( l\) (horizontally) for \( l\) = 16 cm to 1 m. When \( l\) = 60 cm, what is \( \omega\) correct to four significant figures?
________________
The next few problems involve a rod with its lower end in contact with a horizontal table and the rod falling over from an initial vertical (or inclined) position. There are several versions of this problem. The table could be smooth, so that the rod freely slips over the table. Or the lower end could be freely hinged at the table, so that the lower end does not move as the rod falls over. Or the table might be rough, so that the rod might or might not slip.
A uniform rod of mass \( m\) and length \( 2l\) is initially vertical with its lower end in contact with a smooth horizontal table. It is given an infinitesimal angular displacement from its initial position, so that it falls over. When the rod makes an angle \( \theta\) with the vertical, find:
The angular speed of the rod;
The speed at which the centre of the rod is falling;
The speed at which the lower end of the rod is moving;
Show that the speed of the lower end is greatest when \( \theta =\ 37^{\circ}\ 50^{\prime}\).
If the length of the rod is 1 metre, and \( \text{g}\) = 9.8 m s-2, what is the angle \( \theta\) when the speed of the lower end is 1 m s-1?
A uniform rod is initially vertical with its lower end smoothly hinged to a horizontal table. Show that, when the rod falls over, the reaction of the hinge upon the rod is vertical when the rod makes an angle 48o 11' with the vertical, and is horizontal when the rod makes an angle 70o 31' with the vertical.
A uniform rod of length 1 metre, with its lower end smoothly hinged to a horizontal table, is initially held at rest making an angle of 40o with the vertical. It is then released. If \( \text{g}\) = 9.8 m s-1, calculate its angular speed when it hits the table in a horizontal position (easy) and how long it takes to get there (not so easy).
A uniform rod is initially vertical with its lower end in contact with a rough horizontal table, the coefficient of friction being \( \mu\).
Show that:
If \( \mu\) < 0.3706, the lower end of the rod must slip before the rod makes an angle \( \theta\) with the vertical of 35o 05'.
If \( \mu\) > 0.3706, the rod will not slip before \( \theta\) = 51o 15', but it will certainly slip before \( \theta\) = 70o 31' .
If \( \mu\) = 0.25, at what angle \( \theta\) will the lower end slip? If \( \mu\) = 0.75?
It is time for another ladder problem. Most ladders in elementary mechanics problems rest on a rough horizontal floor and lean against a smooth vertical wall. In this problem, both floor and wall are smooth. The ladder starts making an angle of a with the vertical, and then it is released. It immediately starts to slip, of course. After a while it will cease contact with the smooth vertical wall. Show that, at the moment when the upper end of the ladder loses contact with the wall, the angle q that the ladder makes with the vertical is given by \( \cos\theta\ = \frac{2}{3}\cos\alpha\).
If you managed that one all right, this one, which is somewhat similar, should be easy. Maybe.
A uniform solid semicylinder of radius \( a\) and mass \( m\) is placed with its curved surface against a smooth vertical wall and a smooth horizontal floor, its base initially being vertical.
It is then released. Find the reaction \( N_{1}\) of the floor on the semicylinder and the reaction \( N_{2}\) of the wall on the semicylinder when its base makes an angle \( \theta\) with the vertical.
Show that the semicylinder loses contact with the wall when \( \theta\) = 90o, and that it then continues to rotate until its base makes an angle of 39o 46' with the vertical before it starts to fall back.
_________________________
Many problems in elementary mechanics involve a body resting upon or sliding upon an inclined plane. It is time to try a few of these. The first one is very easy, just to get us started. The two following that might be more interesting.
A particle of mass \( m\) is placed on a plane which is inclined to the horizontal at an angle \( \alpha\) that is greater than \( \tan^{-1}\mu\), where \( \mu\) is the coefficient of limiting static friction. What is the least force required to prevent the particle from sliding down the plane?
A cylinder or mass \( m\), radius \( a\), and rotational inertia \( ka^{2}\) rolls without slipping down the rough hypotenuse of a wedge on mass \( M\), the smooth base of which is in contact with a smooth horizontal table. The hypotenuse makes an angle \( \alpha\) with the horizontal, and the gravitational acceleration is \( \text{g}\). Find the linear acceleration of the wedge as it slips along the surface of the table, in terms of \( m,\ M,\ \text{g},\ a,\ k\) and \( \alpha\).
[Note that by saying that the rotational inertia is \( ka^{2}\), I am letting the question apply to a hollow cylinder, or a solid cylinder, or even a hollow or solid sphere.]
A particle is placed on a rough plane inclined at an angle a to the horizontal. It is initially in limiting static equilibrium. It is given an initial velocity \( V_{0}\) along the \( x\)-axis. Ignoring the small difference between the coefficients of moving and limiting static friction, show that at a point on the subsequent trajectory where the tangent to the trajectory makes an angle \( \psi\) with the \( x\)-axis, the speed \( V\) is given by
\( V=\frac{V_{0}}{1+\cos\psi}\)
What is the limiting speed reached by the particle after a long time?
Calculate the moment of inertia of a spherical planet of outer radius \( a\), consisting of a dense core of radius \( xa\) surrounded by a mantle of density \( s\) times the density of the core. Express your answer in the form
\( I=\frac{2}{5}Ma^{2}\times f(x,s)\).
Make sure that, if the density of the core is zero, your expression reduces to the answer you got for Exercise 13.
Draw graphs of \( \frac{I}{(\frac{2}{5}Ma^{2})}\) versus \( x\) (\( x\) going from 0 to 1), for \( s\) = 0.2, 0.4, 0.6 and 0.8.
Show that, for a given mass \( M\) and density ratio \( s\), the moment of inertia is least for a core size give by the solution of
\( 2(I-s)x^{5}+15x^{2}-9=0\)
For a mantle-to-density ratio of 0.6, calculate the core size for which the moment of inertia is least and calculate (in units of \( \frac{2}{5}Ma^{2}\)) the moment of inertia for that core.
Now let’s see if we can determine the core size from a knowledge of the moment of inertia. It is sometimes asserted that one can determine the moment of inertia (and hence the core size) of a planet from the rate of precession of the orbit of a satellite. I am not sure how this would work with a planet such as Mercury, which has never had a satellite in orbit around it. (Mariner 10, while in orbit around the Sun, made three fly-bys past Mercury). Unless a planet departs from spherical symmetry, the orbit of a satellite will not precess, since the gravitational planet is then identical with that from a point mass. And, even if a planet were dynamically oblate, the rate of precession allows us to determine the dynamical ellipticity \( \frac{(C-A)}{C}\), but not either moment of inertia separately.
Nevertheless, let’s suppose that the moment of inertia of a planet is (0.92 ± 1%) % \( \frac{2}{5}Ma^{2}\); specifically, let’s suppose that the moment of inertia has been determined to be between 0.911 and 0.929 % \( \frac{2}{5}Ma^{2}\), and that the mantle-to-core density ratio is known (how?) to be 0.6. Calculate the possible range in the value of the core radius \( x\).
A rectangular brick of length \( 2l\) rests (with the sides of length \( 2l\) vertically) on a rough semicylindrical log of radius \( R\). The drawing below shows three such bricks. In the first one, \( 2l\) is quite short, and it looks is if it is stable. In the second one, \( 2l\) is rather long, and the equilibrium looks decidedly wobbly. In the third one, we’re not quite sure whether the equilibrium is stable or not. What is the longest brick that is stable against small angular displacements from the vertical?
A Thing with a semicylindrical (or hemispherical) base of radius \( a\) is balanced on top of a rough semicylinder (or hemisphere) of radius \( b\) as shown. The distance of the centre of mass of the Thing from the line (or point) of contact is \( l\). Show that the equilibrium is stable if
\( \frac{1}{l}\ >\ \frac{1}{a}+\frac{1}{b}\).
If \( a=b\), is the equilibrium stable if the Thing is
- A hollow semicylinder?
- A hollow hemisphere?
- A uniform solid semicylinder?
- A uniform solid hemisphere?
A log of square cross-section, sides \( 2a\), rests on two smooth pegs a distance \( 2ka\) apart, one of the diagonals making an angle \( \theta\) with the vertical.
Show that, if \( k\ <\ \frac{1}{\sqrt{8}}\ =\ 0.354\) the only equilibrium position possible is \( \theta\) = 90o, but that this position is unstable; consequently, following a small displacement, the log will fall out of the pegs. Show that if the pegs are farther apart, with \( 0.354\ <\ k\ <\ 0.500\), three equilibrium positions are possible. Which of them are stable, and which are unstable? If \( k=0.45\), what are the possible equilibrium values of \( \theta\)? Show that, if \( 0.500\ <\ k\ <\ 1.414\), only one equilibrium position is possible, and that it is stable.
A uniform solid hemisphere of radius \( a\) rests in limiting static equilibrium with its curved surface in contact with a smooth vertical wall and a rough horizontal floor (coefficient of limiting static friction \( \mu\)). Show that the base of the hemisphere makes an angle \( \theta\) with the floor, where
\( \sin\ \theta\ =\ \frac{8\mu}{3}\).
Calculate the value of \( \theta\) if (a) \( \mu\ =\ \frac{1}{4}\) and \( \mu\ =\ \frac{3}{8}\).
What happens if \( \mu\ >\ \frac{3}{8}\)?
A uniform rod of length \( 2l\) rocks to and fro on the top of a rough semicircular cylinder of radius \( a\). Calculate the period of small oscillations.
A uniform solid hemisphere of radius \( a\) with its curved surface in contact with a rough horizontal table rocks through a small angle. Show that the period of small oscillations is
\( P\ =\ 2\pi\sqrt{\frac{26a}{15\text{g}}}\).
The density \( \rho\) of a solid sphere of mass \( M\) and radius \( a\) varies with distance \( r\) from the centre as
\( \rho\ =\ \rho_{0}\left(1-\frac{r}{a}\right)\).
Calculate the (second) moment of inertia about an axis through the centre of the sphere. Express your answer in the form of constant % \( Ma^{2}\).
Two identical particles are connected by a light string of length \( 2a\alpha\). The system is draped over a cylinder of radius \( a\) as shown, the coefficient of limiting static friction being \( \mu\). Determine the angle \( \theta\) when the system is in limiting equilibrium and just about to slide.
Маса\( M\) висить з легкої мотузки, яка проходить над грубим циліндром, коефіцієнт тертя є\( \mu\) і кут колін\( \alpha\). Яке найменше значення\( F\), натягу у верхній частині мотузки, необхідного для запобігання падінню маси?
Дерев'яний куб пливе на воді. Одна з її граней вільно шарнірна до осі, закріпленої в поверхні води. Шарнір фіксується на відстані від верхньої частини грані,\( x\) рівній довжині бічної сторони. Протилежна грань занурюється на відстань, що\( y\) перевищує довжину сторони. Знайдіть відносну щільність\( s\) (тобто щодо щільності води) деревини в перерахунку на\( x\) і \( y\).
Однорідна тверда сфера сидить поверх грубого напівкруглого циліндра. Їй надається невелике зміщення, щоб він скочувався по бічній частині циліндра. Показати, що сфера і циліндр частина компанії, коли лінія приєднання їх центрів робить кут 53 o 58' з вертикаллю.
У школяра трикутний бутерброд зі сторін 9 см, 12 см, 15 см. Вона приймає напівкруглий укус радіусом 3 см з середини гіпотенузи. Де знаходиться центр маси залишку? Це всередині або зовні укусу?
Гумка гумка має довжину\( 2\pi a\) і масу\( m\); постійна сила гуми є\( k\). Смугу перекидають в повітря, обертаючись, так, щоб вона набула вигляду кола, розтягнутого відцентровою силою. (Для цього потрібно багато практики, майстерності та спритності рук.) Знайдіть зв'язок між його радіусом і кутовою швидкістю, в плані\( a,\ m\) і \( k\).
Більшість з нас зробили прості проблеми на тертя в середній школі або на першому курсі в коледжі чи університеті. Ви знаєте, що тіло лежить на грубому горизонтальному столі. До нього прикладається сила. Що відбувається? Спробуйте цей.
Знайдіть рівномірний стрижень АВ. Лінійка буде робити до тих пір, поки вона пряма і не викривлена. Або олівець шестигранного (не круглого) перетину, за умови, що він однорідний і не має гумки на кінці. Помістіть його на грубий горизонтальний стіл. Поступово прикладіть горизонтальне зусилля, перпендикулярне стрижню на кінці А, поки стрижень не почне рухатися. Кінець А буде, звичайно, рухатися вперед. Подивіться на кінець B — він рухається назад. Існує точка С десь уздовж стрижня, який нерухомий. Тобто початковим рухом стрижня є обертання навколо точки С. Обчислити — і виміряти — співвідношення AC/AB. Яку силу ви надаєте на А, коли стрижень ось-ось рухатиметься, з точки зору його ваги та коефіцієнта тертя?
Деякі з більш жахливих проблем тертя - це «Це наконечник чи ковзає?» тип. Це і наступні чотири приклади цього типу.
Однорідний суцільний прямий круговий конус висоти\( h\) і базального радіуса\( a\) розміщений на похилій площині, нахил якого до горизонталі поступово збільшується. Коефіцієнт граничного статичного тертя дорівнює\( \mu\). Конус ковзає, або кінчик?
Кубічний блок боків\( 2a\) спирається на грубий горизонтальний стіл, коефіцієнт граничного статичного тертя якого становить\( \mu\). Поступово збільшується горизонтальна сила прикладається так, як показано на відстані\( x\) над столом. Чи буде блок ковзати або він буде кінчиком? Показати, що, якщо\( \mu\ < \frac{1}{2}\), блок буде ковзати незалежно від значення\( x\).
Циліндричне колода діаметром\( 2a\) і масою\( m\) спирається на два шорстких кілочка (коефіцієнт граничного статичного тертя\( \mu\)) на\( 2ka\) відстані один від одного. Поступово збільшується крутний момент\( \tau\) прикладається, як показано на малюнку. Чи ковзає колода (тобто обертається навколо своєї осі) або кінчик (про правий кілочок)?
Коли ви зробили це, ви можете спробувати варіант (який я не розробив і не розмістив рішення), в якому циліндр радіусу\( a\) спирається на бордюр (або бордюр, якщо ви віддаєте перевагу такому написанню) висоти\( h\), і крутний момент застосовується. Чи буде це кінчик чи буде ковзати?
Ця проблема виявляє серйозні обмеження моїх художніх здібностей, але малюнок вище, вірте чи ні, являє собою автомобіль, побачений ззаду. Можна побачити водія і пасажира. Висота центру маси дорівнює,\( h\) а відстань між колесами дорівнює\( 2d\). Автомобіль рухається по горизонтальному дорожньому покриттю\( \mu\), коефіцієнт тертя, і рулить ліворуч по колу радіуса\( R\), центр кривизни знаходиться далеко зліва від креслення. У міру того, як вони поступово збільшують свою швидкість, чи буде автомобіль ковзати вправо, або вона перекинеться через праве маховик, і на якій швидкості відбудеться ця катастрофа? На щастя, водій і пасажир обидва носили ремені безпеки, і жоден з них не постраждав, і ніколи більше не їхали занадто швидко за кут.
Рівномірний стрижень довжини\( 2l\) спирається на стіл, при цьому довжина\( l-a\) стикається зі столом, а залишок,\( l+a\) стирчить через край — тобто відстань від краю столу до середини стрижня.\( a\) Спочатку він запобігає падінню силою, як показано на малюнку. Коли зусилля знімається, стрижень повертається приблизно А. показати, що стрижень ковзає, коли робить кут\( \theta\) з горизонталлю, де
\( \tan\ \theta\ =\ \frac{2\mu}{2\ +\ 9(\frac{a}{l})^{2}}\)
Тут m - коефіцієнт граничного статичного тертя при А.
Гнучка ланцюг маси\( m\) і довжини спочатку\( l\) знаходиться в стані спокою, причому одна її половина спирається на гладкий горизонтальний стіл, а інша половина звисає через край:
Його відпускають, щоб вона почала сповзати зі столу. У наступний час\( t\) довжина\( \frac{1}{2}l-x\) залишається в контакті зі столом, що залишилася довжина\( \frac{1}{2}l+x\) звисає вертикально, а швидкість ланцюга дорівнює\( v\).
Покажіть, що
\( v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}\),
\( x\ =\ \frac{l(e^{\sqrt{\frac{\text{g}}{lt}}}-1)^{2}}{4e^{\sqrt{\frac{\text{g}}{lt}}}}\)
\( v\ =\ \frac{\sqrt{\text{g}l}(e^{\sqrt{\frac{\text{4g}}{lt}}}-1)}{4e^{\sqrt{\frac{\text{4g}}{lt}}}}\)
Чотири книги, кожна шириною\( 2w\), укладаються один на одного купкою, таким чином:
Який максимально можливий звис,\( D\)?
Скільки книг знадобиться, щоб домогтися звису\( 10w\)?
З огляду на необмежений запас книг, який максимальний звис досяжний?
Людина і собака.
У той час\(t = 0\), Людина знаходиться біля початку координат, і він починає ходити вгору по\(y\) -осі з постійною швидкістю\(v\). Собака починається\((a , 0) \) і біжить з постійною швидкістю\(Av (v > 1)\) до Людини. Швидкість Собаки завжди спрямована прямо в сторону Людини. Знайдіть рівняння для шляху, який переслідує Собака, і намалюйте графік цього шляху. Як далеко пройшов Людина, коли Собака досягає Людини, і скільки часу це займає?
Частинка А маси\(m\) прикріплюється світлою струною до другої частинки, В, також маси\(m\). А спирається на гладкий горизонтальний стіл, в той час як Б висить вертикально через отвір в столі. За часом нуль довжина горизонтальної частини струни (тобто відстань А від отвору) дорівнює a, а А рухається по столу в горизонтальному колі радіусом a з початковою кутовою швидкістю\( \omega_0\).
У якийсь наступний час довжина горизонтальної частини струни дорівнює\(r\) і кутова швидкість А дорівнює\( \omega \). Позначимо темпом збільшення\(r\) з часом, який, очевидно, буде негативним, якщо B падає.
Показати,\( \dot{r} \) що дається
\[ \frac{\dot{r}^2}{ga} = 1 + \frac{a \omega^2_0}{2g} \left( 1- \frac{\omega}{\omega_0}\right) - \sqrt{\frac{\omega}{\omega_0}}. \label{eq:1} \]
Покажіть, що, якщо\(a \omega^2_0 = g \), де\( \Omega = \omega \ \omega_0 \).
\[ \frac{ \dot{r}^2}{ga} = \frac{3}{2} - \frac{1}{2} \Omega - 1 / \sqrt{\Omega} , \label{eq:2} \]
Показати, що існує тільки одне значення Ω, а саме 1, для якого існує реальне рішення для\( \dot{r} \), а саме\( \dot{r} = 0 \). Це означає, що система залишається в рівновазі, при цьому радіус кола, кутова швидкість А і висота В залишаються постійними, при цьому відцентрова сила на А залишається рівною вазі B.
Покажіть, що якщо\( a \omega^2_0 = 2g \),
\( \frac{\dot{r}^2}{ga} = 2 - \Omega - 1 / \sqrt{ \Omega} \)
і що А рухається назовні (його кутова швидкість зменшується) і B рухається вгору,
досягнення максимальної швидкості\( \dot{r} = 0.331841 \sqrt{ga} \)
де\( \dot{r} = 1.259921 a \)
коли\( \omega = 0.629961 \omega_0, \)
і досягає рівноваги, коли\( \dot{r} = 0 \)
де\( \dot{r} = 1.618034a \)
коли\( \omega = 0.381966 \omega_0. \)
Покажіть, що якщо\( a \omega^2_0 = \frac{1}{2}g\),
\( \frac{ \dot{r}^2}{ga} = \frac{5}{4} - \frac{1}{4} \Omega - 1 / \sqrt{ \Omega} ,\)
і що A рухається всередину (його кутова швидкість збільшується), а B рухається вниз,
досягнення максимальної швидкості\( \dot{r} = -0.243822 \sqrt{ga} \)
де\( r = 0.793701 a \)
коли\( \omega = 1.587401 \omega_0, \)
і досягає рівноваги, коли\( \dot{r} = 0\)
де\( r = 0.640338a\)
коли\( \omega = 2.438447 \omega_0. \)
Цю задачу — біфілярний торсіонний маятник — запропонував мені Клод Платі, який використовував метод у практичному застосуванні для визначення обертальної інерції (моменту інерції) реального неоднорідного стрижня. Він також звернув мою увагу на цікаву статтю про визначення моментів інерції тіл (типу літальних апаратів!) за методом: naca.larc.nasa.gov/digidoc/re... ACA-TR-467.PDF
Симетричний, але не обов'язково рівномірний стрижень маси\(m\) і моменту інерції\(I\) підвішується до стелі двома легкими нитками кожної довжини на\(L\)\(D\) відстані один від одного\( (D << L )\). Стрижень скручується навколо вертикальної осі через його середину через невеликий кут, а потім випущений. Знайти період малих коливань в горизонтальній площині.
Йо-йо має масу М і обертальну інерцію\(I\). Радіус його осі дорівнює\(a\), і падає він звичайним способом з довжиною струни, обмотаної навколо осі.
Як це його лінійне прискорення вниз
\( \frac{Ma^2}{Ma^2 + I} \times g \)
і що натяг в струні i
\(\frac{I}{Ma^2+ 1} \times Mg \)
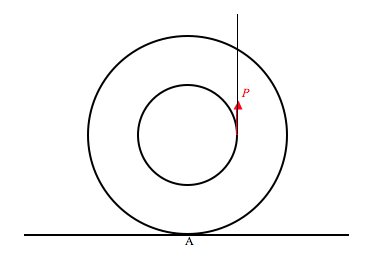
Йо-йо, маса\(M\), радіус осі\(a\), зовнішній радіус\(b\), спирається на горизонтальний стіл, як показано на малюнку. Струна, обмотана навколо осі, тримається вертикально, як показано на малюнку, і\(P\) прикладається зусилля. Коефіцієнт тертя між йо-йо і столом дорівнює\( \mu \). Покажіть, що, якщо
\( \mu > \frac{MabP}{(Mg-P)(I + Mb^2}, \)
початковим рухом йо-йо буде котитися вліво без ковзання, з початковим лінійним прискоренням
\( \frac{abP}{I + Mab} ; \)
але що якщо
\( \mu < \frac{MabP}{(Mg-P)(I + Mb^2}, \)
йо-йо буде обертатися проти годинникової стрілки без кочення, з початковим кутовим прискоренням близько С
\( \frac{P(a - \mu) - \mu Mg }{I}. \)

Йо-йо, маса\( M\), радіус осі\( a\), зовнішній радіус\( b\), спирається на горизонтальний стіл, як показано на малюнку. Струна, обмотана навколо осі, тримається горизонтально, як показано на малюнку, і\( P\) прикладається зусилля. Коефіцієнт тертя між йо-йо і столом дорівнює\( \mu\).
(i) Показати, що, якщо\( I>Mab\):
Якщо
\( \mu\ >\ \left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\)
початковим рухом йо-йо буде котитися вправо без ковзання, з початковим лінійним прискоренням
\( \frac{Pb(a+b)}{I+Mb^{2}}\);
але що, якщо
\( \mu\ <\ \left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\),
йо-йо одночасно розганяється вправо з лінійним прискоренням
\( \frac{P-\mu M\text{g}}{M}\)
при цьому відбувається кутове прискорення за годинниковою стрілкою близько С
\( \frac{Pa\ +\ \mu M\text{g}b}{I}\).
(ii) Показати, що, якщо\( I>Mab\):
Якщо
\( \mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)\),
початковим рухом йо-йо буде котитися вправо без ковзання, з початковим лінійним прискоренням
\( \frac{Pb(a+b)}{I+Mb^{2}}\);
але що, якщо
\( \mu\ <\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)\),
йо-йо одночасно розганяється вправо з лінійним прискоренням
\( \frac{P\ +\ \mu M\text{g}}{M}\)
при цьому відбувається кутове прискорення за годинниковою стрілкою близько С
\( \frac{Pa\ -\ \mu M\text{g}b}{I}\).
(iii) Показати, що, якщо\( I>Mab\):
(Після завдання 40 (b) це набагато простіше і бажане полегшення.)
Йо-йо, маса\( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held horizontally as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is m.
Show that, if
\( \mu\ >\ \left(\frac{I+Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\),
the initial motion of the yo-yo will be to roll to the right without slipping, with an initial linear acceleration
\( \frac{Pb(b-a)}{I+Mb^{2}}\)
and angular acceleration
\( \frac{P(b-a)}{I+Mb^{2}}\)
but that, if
\( \mu\ <\ \left(\frac{I+Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\)
the yo-yo slips at A. C accelerates to the right at a rate of \( \frac{P-\mu M\text{g}}{M}\), while the yo-yo spins around C with a counterclockwise angular acceleration of \( \frac{Pa-\mu M\text{g}b}{I}\).
A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held at an angle \( \theta\) to the horizontal as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).
The complete analysis of this problem is similar to that of Problem 40(b), except that a factor of \( \cos\theta\) appears in many of the equations. No new phenomena appear, and the analysis is tedious without any new points of interest. For that reason I limit this problem to asking you to show that the direction of the frictional force of the table on the yo-yo at A depends upon whether the \( \cos\theta\) is less than or greater than \( \frac{Mab}{I}\).
A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held at an angle \( \theta\) to the horizontal as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).
Show that, provided there is no slipping, the yo-yo rolls to the right if \( \cos\theta>\frac{a}{b}\) and to the left if \( \cos\theta<\frac{a}{b}\). Describe what happens if \( \cos\theta=\frac{a}{b}\).
A uniform plane lamina of mass \( 3m\) is in the form of a truncated square like the one above.
Find the position of the centre of mass, the principal moments of inertia with respect to the centre of mass, and the eccentricity and inclination of the momental ellipse.
A mass \( M\) sits on a smooth horizontal table. A second mass, \( m\), hangs from the first by a light inextensible string. A slot in the table allows \( m\) and the string to swing as a pendulum.
The system is then set in motion with the pendulum swinging, and the mass \( M\) sliding back and forth on the table. At some instant when the horizontal displacement of \( M\) from its equilibrium position is \( x\) the string makes an angle \( \theta\) with the vertical.
Show that the equations of motion are
\( (M+m)\ddot{x}\ +\ ml(\ddot{\theta}\cos\theta\ -\ \dot{\theta}^{2}\sin\theta)\ =\ 0\),
\( I\ddot{\theta}\ +\ \ddot{x}\cos\theta\ -\ \dot{x}\sin\theta\dot{\theta}\ =\ -\text{g}\sin\theta\).
Show that for small oscillations \( (\cos\theta\approx 1,\ \sin\theta\approx\theta,\ \dot{\theta}^{2}\theta<<\ddot{\theta},\ \dot{x}\theta\dot{\theta}<<\text{g})\) the period the motion is approximately \( 2\pi\sqrt{\frac{Ml}{(M+m)\text{g}}}\). Note that, if \( m<<M\), this reduces to \( 2\pi\sqrt{\frac{l}{\text{g}}}\) as expected.
A gun projects a shell, in the absence of air resistance, at an initial angle to the horizontal. The speed of projection varies with the angle \( \alpha\) of projection and is given by
initial speed = \( V_{0}\cos\frac{1}{2}\alpha\).
Show that, in order to achieve the greatest range on the horizontal plane, the shell should be projected at an angle to the horizontal whose cosine \( c\) is given by the solution of the equation
\( 3c^{3}+2c^{2}-2c-1=0\)
and determine this angle to the nearest arcminute.
The length of a cylindrical log is \( L\) times its diameter, and its density is \( s\) times that of water \( (0<s<1)\). Show that the log can float vertically in stable equilibrium, whatever its density, provided that \( L<0.707\). and that, if its length is greater than this, it can float vertically in stable equilibrium only if
\( L<\frac{1}{\sqrt{8s(1-s)}}\).
Show that, if the length is equal to the diameter, it can float in stable equilibrium with its cylindrical axis vertical only if its density is less than 0.146 or greater than 0.854 times that of water.
A uniform heavy rod of length 6 hangs from a fixed point C by means of two light strings of lengths 4 and 5. What angle does the rod make with the horizontal?
Incidentally, a (4, 5, 6) triangle has the interesting property that one of its angles is exactly twice one of the other ones.
A uniform rod rests on two smooth (frictionless) planes inclined at 30º and 45º to the horizontal. What angle does the rod make with the horizontal?
A uniform rod of length \( 2l\) rests on the inside of a circular cylindrical pipe of radius \( a\). The coefficient of limiting static friction (often known for short, if with less precision, as “the”coefficient of friction) \( \mu\). What is the maximum angle \( \theta\) that the rod can make with the horizontal in static equilibrium?
