17.10: Вода

Вода складається з маси$M$ («кисню»), з'єднаної з двома меншими рівними масами$m$ («воднем») двома рівними пружинами силових постійних$k$, кут між пружинами якого є$2\theta$. Рівноважна довжина кожної пружини дорівнює$r$. Крутний момент, необхідний для збільшення кута між пружинами на$2\delta \theta$ є$2c\delta \theta$. Див. Рисунок XVII.10. ($\theta$становить близько 52°.)

У будь-який час нехай координати трьох мас (зліва направо) будуть

$(x_1,y_1), \qquad (x_2,y_2), \qquad (x_3,y_3)$

і нехай положення рівноваги

$(x_{10},y_{10}), \qquad (x_{20},y_{20}), \qquad (x_{30},y_{30}), \text{ where} y_{30} = y_{10}$

Ми припускаємо, що ці координати відносяться до кадру, в якому центр маси системи нерухомий.

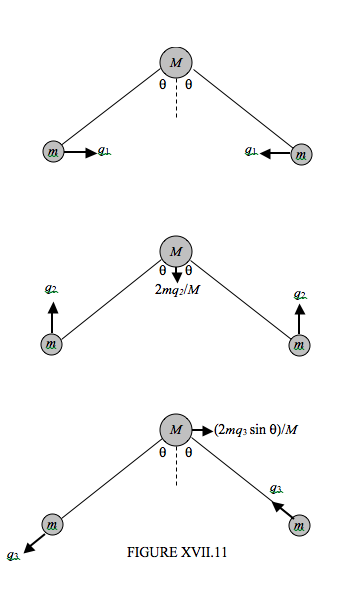
Спробуємо уявити, на малюнку XVII.11, коливальні режими. Ми можемо легко уявити собі режим, при якому кут відкривається і закривається симетрично. Дозвольте вирішити цей режим у$x$ -commonent та$y$ -commonent. У$x$ -компоненті цього руху один атом водню рухається вправо на відстань,$q_1$ а інший рухається вліво на рівну відстань$q_1$. У$y$ -компоненті цього симетричного руху обидва водню рухаються вгору на відстань$q_2$, в той час як, щоб центр маси системи не рухався, кисень обов'язково рухається вниз на відстань$2mq_2/M$. Ми також можемо уявити асиметричний режим, в якому одна пружина розширюється, а інша стискається. Один водень рухається вліво на відстань$q_3$, а інший рухається вгору вліво на ту ж відстань. Тим часом кисень повинен рухатися вправо на відстань$(2mq_3 \sin \theta )/M$, щоб центр маси не рухався.

Ми спробуємо записати кінетичну та потенційну енергії з точки зору внутрішніх координат$q_1, q_2$ і$q_3$.

Легко записати кінетичну енергію за$(x , y)$ координатами:

$$T\ =\ \frac{1}{2}m(\dot{x}_{1}^{2}\ +\ \dot{y}_{1}^{2})\ +\ \frac{1}{2}M(\dot{x}_{2}^{2}\ +\ \dot{y}_{2}^{2})\ +\frac{1}{2}m(\dot{x}_{3}^{2}\ +\ \dot{y}_{3}^{2}). \label{17.10.1}$$

З геометрії ми маємо:

$$\begin{align} \dot{x}_{1} &=\ \dot{q}_{1}-\dot{q}_{3}\sin\theta \\[5pt] \dot{y}_{1} &= \dot{q}_{2}-\dot{q}_{3}\cos\theta \label{17.10.2a,b} \\[5pt] \dot{x}_{2} &= \frac{2m\dot{q}_{3}\sin\theta}{M} \\[5pt] \dot{y}_{2} &= -\frac{2m\dot{q}_{2}}{M} \label{17.10.3a,b} \\[5pt] \dot{x}_{3} &= -\dot{q}_{1} - \dot{q}_{3}\sin\theta \\[5pt] \dot{y}_{3} &= \dot{q}_{2}\ +\ \dot{q}_{3}\cos\theta \label{17.10.4a,b} \end{align}$$

Поклавши їх у рівняння,$\ref{17.10.1}$ отримаємо

$$T\ =\ m\dot{q}_{1}^{2}\ +\ m\left(1+\frac{2m}{M}\right)\dot{q}_{2}^{2}\ +\ m\left(1+\frac{(2m\sin^{2}\theta)}{M}\right)\dot{q}_{3}^{2} \label{17.10.5}$$

Коротше кажучи, я збираюся написати це як

$$T=a_{11}\dot{q}_{1}^{2}+a_{22}\dot{q}_{2}^{2}+a_{33}\dot{q}_{3}^{2} \label{17.10.6}$$

Тепер про потенційну енергію.

Подовження лівої пружини

$$\delta r_{1}=-q_{1}\sin\theta-q_{2}\cos\theta-\frac{2mq_{2}\cos\theta}{M}+q_{3}+\frac{2mq_{3}\sin\theta\cos\theta}{M}\\=-q_{1}\sin\theta-q_{2}\left(\frac{1+2m}{M}\right)\cos\theta+q_{3}\left(1+\frac{(2m\sin^{2}\theta)}{M }\right) \label{17.10.7}$$

Розширення правої пружини

$$\delta r_{2}=-q_{1}\sin\theta-q_{2}\cos\theta-\frac{2mq_{2}\cos\theta}{M}-q_{3}-\frac{2mq_{3}\sin^{2}\theta}{M}\\=-q_{1}\sin\theta-q_{2}\left(\frac{1+2m}{M}\right)\cos\theta-q_{3}\left(1+\frac{(2m\sin^{2}\theta)}{M }\right). \label{17.10.8}$$

Збільшення кута між пружинами становить

$$2\delta\theta=-\frac{2q_{1}\cos\theta}{r}\ +\ \frac{2(1+\frac{2m}{M})q_{2}\sin\theta}{r}. \label{17.10.9}$$

Потенційна енергія (вище положення рівноваги)

$$V=\frac{1}{2}k(\delta r_{1})^{2}\ +\ \frac{1}{2}k(\delta r_{2})^{2}\ +\ \frac{1}{2}c(2\delta\theta)^{2}. \label{17.10.10}$$

Про підстановці рівнянь$\ref{17.10.7}$,$\ref{17.10.8}$ а$\ref{17.10.9}$ в це отримуємо рівняння виду

$$V=b_{11}q_{1}^{2}\ +\ 2bq_{12}q_{1}q_{2}\ +\ b_{22}q_{2}^{2}\ +\ b_{33}q_{3}^{2}, \label{17.10.11}$$

де я залишаю його читачеві, якщо він/вона бажає, опрацювати докладні вирази для коефіцієнтів. У нас все ще є перехресний член, тому ми не можемо повністю розділити координати, але ми можемо легко застосувати рівняння Лагранжа до рівнянь\ ref {17.10.6} і\ ref {17.10.11}, а потім шукати прості гармонічні рішення звичайним способом. Встановлення визначника коефіцієнтів в нуль призводить до наступного рівняння для кутових частот нормальних режимів:

$$\begin{bmatrix}b_{11}-\omega^{2}a_{11} & b_{12} & 0 \\ b_{12} & b_{22}-\omega^{2}a_{22} & 0\\ 0 & 0 & b_{33}-\omega^{2}a_{33} \end{bmatrix}\ =\ 0. \label{17.10.12}$$

Таким чином, враховуючи маси$r, \theta, k$ і і$c$, можна передбачити частоти нормальних режимів. Чи можна обчислити$k$ і$c$ задати частоти? Не знаю, по правді кажучи. Чи можу я залишити це читачеві для подальшого дослідження?