6.3B: Тіло, що потрапляє під силу тяжіння в опорному середовищі, резистивна сила пропорційна швидкості

Ми тут, мабуть, розглядаємо невелику сферу, яка повільно падає через в'язку рідину, з ламінарним потоком навколо сфери, а не парашутист, що мчить по повітрю. В останньому випадку потік повітря, швидше за все, буде сильно турбулентним, а опір пропорційно більшій потужності швидкості, ніж перший.

Ми будемо використовувати символ\( y\) для відстані, що впав. Тобто ми вимірюємо\( y\) вниз від початкової точки. Рівняння руху є

\[ \ddot{y}= g - \gamma v, \tag{6.3.8}\label{eq:6.3.8} \]

де\( g\) - гравітаційне прискорення.

Тіло досягає постійної швидкості, коли\( \ddot{y}\) стає нулем. Це відбувається зі швидкістю\( \hat{v}=\frac{g}{\gamma} \), яка називається термінальною швидкістю.

Для отримання першого інтеграла запишемо рівняння руху як

\[ \frac{dv}{dt} = \gamma( \hat{v} -v) \tag{6.3.9}\label{eq:6.3.9} \]

або

\[ \frac{dv}{ \hat{v} -v} = \gamma dt. \tag{6.3.10}\label{eq:6.3.10} \]

\ [
\ frac {dv} {v -\ hat {v}} = -\ гамма dt. \ tag {6.3.11}\ етикетка {еква:6.3.11}\]

НЕ ТРЕБА! В середині іспиту, охоплюючи цю деривацію, яку ви так добре знаєте, ви можете раптом опинитися в нерозривних труднощах. Слід зазначити, що це. Якщо ви подивитеся на ліву частину рівняння, ви очікуєте, що логарифм з'явиться, коли ви його інтегруєте. Тримайте знаменник позитивним! Деякі математики можуть знати значення логарифма від'ємного числа, але більшість з нас звичайні смертні цього не роблять - так що тримайте знаменник позитивним!

При початковій\( v=0\) умові коли \( t=0\), перший раз інтеграл стає

\[ v = \hat{v}(1-e^{\gamma t}). \tag{6.3.12}\label{eq:6.3.12} \]

Це проілюстровано на малюнку VI.5.

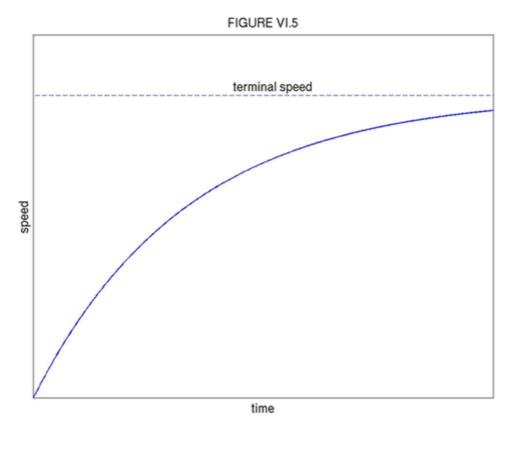
Студенти бачили рівняння, подібні до цього раніше в інших галузях фізики - наприклад, зростання заряду в конденсаторі або зростання струму в індукторі. Ось чому вивчати фізику постійно стає простіше, адже ви бачили все це раніше в зовсім інших контекстах. Можливо, ви вже помітили, що фізика третього курсу легше, ніж фізика другого курсу; просто подумайте, наскільки легше буде четвертий рік! У будь-якому випадку,\( v\) наближається до швидкості терміналу асимптотично, ніколи не досягаючи її, але досягаючи половини швидкості терміналу в часі\( \frac{\ln2}{\gamma}=\frac{.693}{\gamma}\) (ви бачили це раніше під час вивчення радіоактивного розпаду), і досягаючи (\( 1-e^{-1}\)) = 63% швидкості терміналу в часі\( \frac{1}{\gamma}\).

Якщо тіло кидається вниз, так що його початкова швидкість не дорівнює нулю, а\( v=v_{0}\) коли\( t=0\), ви запишете рівняння руху або як рівняння,\( \ref{eq:6.3.10}\) або як рівняння\( \ref{eq:6.3.11}\), залежно від того, чи є початкова швидкість повільнішою або швидшою за швидкість терміналу, тим самим забезпечуючи це знаменник тримається твердо позитивним. У будь-якому випадку результат

\[ v = \hat{v}+(v_{0} -\hat{v})e^{-\gamma t} \tag{6.3.13}\label{eq:6.3.13} \]

На малюнку VI.6 показано\( v\) як функцію\( t\) для початкових умов\(v_{0} = 0, \frac{1}{2}\hat{v},\hat{v}, 2\hat{v}\).

Повертаючись до початкової умови \( t=0\),\( v=0\) коли, ми з готовністю знаходимо другий раз інтеграл бути

\[ y = \hat{v}t - \frac{\hat{v}}{\gamma}(1-e^{-\gamma t}). \tag{6.3.14}\label{eq:6.3.14} \]

Ви повинні перевірити, чи є це рівняння тим, що очікується, коли\( t=0\) і коли\( t\) наближається до нескінченності. Другий раз інтеграл показаний на малюнку VI.7.

Просторовий інтеграл знаходить або шляхом усунення t між першим і другим інтегралами часу, або шляхом запису\( \ddot{y} \) як\( v\frac{dv}{dy}\) у рівнянні руху:

\[ v\frac{dv}{dy}= \gamma(\hat{v}-v), \tag{6.3.15}\label{eq:6.3.15} \]

звідки

\[ y = \frac{\hat{v}}{\gamma}\ln(1-\frac{v}{\hat{v}}) - \frac{v}{\gamma}. \tag{6.3.16}\label{eq:6.3.16} \]

Це проілюстровано на малюнку VI.8. Зверніть увагу, що рівняння дає\( y\) як функцію\( v\), але тільки

числовий розрахунок дасть \( v\)для заданого\( y\).

Вправа\(\PageIndex{1}\)

Припустимо\( g\) = 9,8 м с ^-2. Частка, починаючи з відпочинку, скидається через середовище таке, що швидкість терміналу становить 9,8 м с ^-1. Скільки часу знадобиться, щоб провалитися через 9,8 м?

Рішення

Нас просять\( t\), дано\( y\), і ми знаємо рівняння, що стосується\( t\) і\( y\) - це другий раз інтеграл, Рівняння\( \ref{eq:6.3.14}\) - так що може бути простіше? У нас є\( \gamma=\frac{g}{\hat{v}}\) = 1s ⁻¹, тому рівняння\( \ref{eq:6.3.14}\) стає

\[ 9.8 = 9.8t -9.8(1-e^{-t}) \tag{6.3.17}\label{eq:6.3.17} \]

і раптом ми виявляємо, що це не так просто, як очікувалося!

Рівняння можна записати

\[ f(t) = t + e^{-t} -2 =0. \tag{6.3.18}\label{eq:6.3.18} \]

Для ітерації Ньютона-Рафсона нам потрібно

\[ f'(t) = 1 - e^{-t}. \tag{6.3.19}\label{eq:6.3.19} \]

і, після деякої перестановки, ітерація Ньютона-Рафсона\( (t\rightarrow t-\frac{f}{f'})\) стає

\[ t = \frac{1-t}{e^{t} - 1}+2. \tag{6.3.20}\label{eq:6.3.20} \]

(Можна помітити\( \ref{eq:6.3.20}\), що, що випливає з процесу Ньютона-Рафсона, є лише перебудовою рівняння\( \ref{eq:6.3.18}\).)
Починаючи з надзвичайно дурного першого припущення\( t\) = 100 с, ітерації протікають наступним чином:

\( t\)= 100.000 000 000

2.000 000 000

1,843 482 357

1,841 406 066

1,841 405 661

1 841 405 660 сек

Вправа\(\PageIndex{2}\)

Припустимо\( g\) = 9,8 м с ^-2. Частинка, починаючи з спокою, потрапляє через опір середовища, при цьому демпфіруюча\( \gamma\) константа дорівнює 1,96 с ^-1 (тобто\( \hat{v} \) = 5 м с ^-1). Як швидко він рухається після того, як впав на 0,3 м?

Рішення

Нас просять\( v\), дано\( y\). Ми хочемо, щоб простір інтеграл, Рівняння\( \ref{eq:6.3.16}\). На підстановці даних отримуємо

\[ f(v) = 5\ln(1-0.2v)+ v+0.588 = 0. \tag{6.3.21}\label{eq:6.3.21} \]

З цього,

\[ f'(v) = v/(v-5) \tag{6.3.22}\label{eq:6.3.22} \]

Процес Ньютона-Рафсона\( (t\rightarrow t-\frac{f}{f'})\), після деякої алгебри, прибуває

\[ v = \frac{u(5\ln(0.2u)+0.588)}{v}+ 5= \frac{u(5\ln u-7.459189560)}{v}+5, \tag{6.3.23}\label{eq:6.3.23} \]

де\( u=5-v\).

Цього разу Ньютон-Рафсон не дозволяє нам розкоші надзвичайно дурного першого припущення, але ми знаємо, що відповідь повинна лежати між 0 і 5 м ^-1, тому наша помірно розумна перша здогадка може бути\( v\) = 2.5ms ^-1.

Ітерації Ньютона-Рафсона:

\( v\)= 2.500 000 000

2.12 264 100

2.051 880 531

2.049 766 247

2.049 764 400 м с ^-1

Проблеми

Ось чотири проблеми, що стосуються тіла, що падає з відпочинку, такі, що опір пропорційний швидкості. Припустимо, що\( v\) = 9.8 m s ⁻². Відповіді на питання 6.3.3 - 6.3.6 повинні бути дані з точністю 0,0001 секунди.

Вправа\(\PageIndex{3}\)

Частинка падає з спокою в середовищі таким чином, що демпфіруюча\( \gamma\) константа дорівнює 1,0 с ⁻¹. Скільки часу знадобиться, щоб провалитися через 10 м?

Вправа\(\PageIndex{4}\)

Це займає\( t\) секунди, щоб провалитися через\( y\) метри. Побудувати таблицю, яка\( t\) показує 201 значення\( y\) переходу від 0 до 20 метрів з кроком 0,1 метра, припускаючи, що\( \gamma\) = 1,0 с ⁻¹.

Вправа\(\PageIndex{5}\)

Побудувати таблицю, що\( t\) показує 201 значення\( y\) переходу від 0 до 20 метрів з кроком 0,1 метра для\( \gamma\) = 0,0, 0,5, 1,0, 1,5, 2,0 с. Таблиця повинна мати шість стовпців. Перший стовп дає відстань, що впав з точністю до 0,1 метра. Решта п'ять стовпців дадуть час, з точністю 0,0001 секунди, який тіло приймає, щоб впасти на задану відстань, з точністю 0,0001 секунди

Вправа\(\PageIndex{6}\)

Намалюйте за допомогою комп'ютера графік, що показує\( t\) (залежна змінна, побудована вертикально) проти y (побудована горизонтально) для п'яти значень\( \gamma\) розглянутого питання 3.

Ці чотири проблеми в порядку збільшення складності. Перший є лише вправою у вирішенні неявного рівняння (рівняння\( \ref{eq:6.3.14}\)) чисельно, і може служити вступним прикладом того, як, наприклад, вирішити рівняння за допомогою ітерації Ньютона-Рафсона (я роблю відповідь 1.8656 с.) Останні два, якщо почати з нуля, цілком могли б зайняти цілий день, перш ніж це буде вирішено до повного задоволення. Можна помітити, що графіки питання 4 можуть бути намальовані досить легко, обчислюючи\( y\) явно як функцію\( t\), тим самим усуваючи необхідність ітерації Ньютона-Рафсона. Ніяких таких коротких скорочень, однак, не можна зробити для побудови таблиці питання 3.

Насправді я вирішував питання 3 і 4 всього за кілька хвилин - але я не почав з нуля. Коли ви прогресуєте через свою наукову кар'єру, ви будете усвідомлювати, що існують певні операції, з якими ви стикаєтеся знову і знову. Наприклад, щоб зробити питання 3 і 4, ви повинні бути в змозі вирішити рівняння за допомогою ітерації Ньютона-Рафсона; ви повинні бути в змозі побудувати таблицю функції\( y=f(x\quad;\quad a)\), або в цьому випадку\( t=f(y\quad;\quad \gamma)\); і ви повинні бути в змозі доручити комп'ютера малювати графіки табличних значень. Я давно дізнався, що все це проблеми, які виникають часто, і тому я давно написав короткі програми (всього кілька рядків Fortran кожна) для виконання кожної з них. Все, що мені потрібно було зробити з цього приводу, це одружитися з цими існуючими програмами разом, пристосованими до конкретних функцій, необхідних. Так само студент визнає подібні проблеми, для яких він або вона часто потребує вирішення. Ви повинні накопичувати та зберігати набір цих невеликих програм для використання в майбутньому, коли вони вам можуть знадобитися. Наприклад, це аж ніяк не останній раз, коли вам знадобиться ітерація Ньютона-Рафсона для вирішення рівняння. Напишіть програму Ньютон-Рафсона зараз і збережіть її для майбутніх випадків!