Skip to main content
LibreTexts - Ukrayinska

6.3A: Тільки резистивна сила

  1. Last updated
  2. Save as PDF
  • Page ID
    76200

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Важко уявити реальну ситуацію, в якій єдина сила - це резистивна сила, пропорційна швидкості. Тіло, що падає через повітря, не зробить, тому що, крім резистивної сили, є прискорення за рахунок сили тяжіння. Можливо, ми могли б уявити собі шайбу, що ковзає по льоду. Лід потрібно було б вважати повністю без тертя, і єдиною силою на шайбу буде опір повітря. Це трохи штучна ситуація, тому що ми хочемо, щоб шайба йшла так швидко, що сила тертя незначна порівняно з опором повітря, але не настільки швидка, щоб потік повітря був турбулентним - але нам потрібно десь починати. Сила тертя, принаймні, до дуже хорошого наближення, не є функцією швидкості, але постійною, і ми почнемо з припущення, що вона незначна і що єдиною горизонтальною силою на шайбі є опір повітря і що опір повітря пропорційний швидкості.

    У цьому випадку рівняння руху дійсно є рівнянням 6.3.2. Щоб отримати перший раз інтеграл, ми пишемо\( \dot{x}\) як\( v\) і перший раз інтеграл легко знайти бути

    \[ v = v_{0}e^{-\gamma t}. \tag{6.3.3}\label{eq:6.3.3} \]

    \( v_{0}\)Ось початкова швидкість. Це проілюстровано на малюнку VI.2

    альт

    Швидкість зменшується до половини початкової швидкості за раз

    \[ t_{\frac{1}{2}} = \frac{\ln2}{\gamma} = \frac{0.693}{\gamma}. \tag{6.3.4}\label{eq:6.3.4} \]

    Другий раз інтеграл знаходять шляхом написання\( v\) в Equation\( \ref{eq:6.3.3}\) as\( \frac{dx}{dt}\). Інтеграція, з початковою умовою\( t = 0\),\( x = 0\) коли, дає

    \[ x = x_{∞}(1-e^{-\gamma t}), \tag{6.3.5}\label{eq:6.3.5} \]

    де\( x_{\infty}=\frac{v_{0}}{\gamma}\). Це проілюстровано на малюнку VI.3. Видно, що шайба подорожує на можливу відстань\( x_{\infty}\), але лише через нескінченний час.

    альт

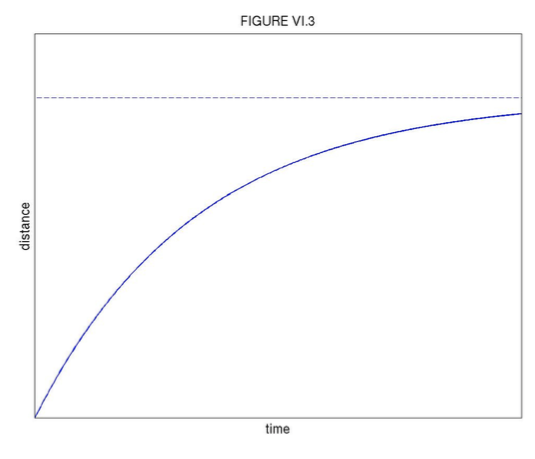
    Ми можемо отримати просторовий інтеграл або шляхом усунення\( t\) між двома часовими інтегралами, або шляхом написання Рівняння руху як

    \[ v\frac{dv}{dx} = - \gamma v. \tag{6.3.6}\label{eq:6.3.6} \]

    При початковому стані\( v = v_{0}\) коли\( x = 0\), це стає

    \[ v = v_{0} - \gamma x, \tag{6.3.7}\label{eq:6.3.7} \]

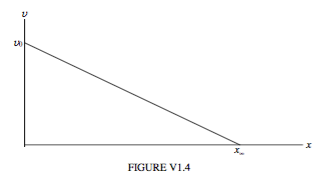
    який проілюстрований на малюнку VI.4. Швидкість падає лінійно, коли відстань (але експоненціально з часом) досягає нуля після того, як пройшла скінченну відстань\( x_{\infty}=\frac{v_{0}}{\gamma}\) за нескінченний час.

    альт

    Цей аналіз припускав, що єдиною силою була резистивна сила, пропорційна швидкості. Що стосується нашої уявної шайби льоду, ми припускали, що резистивна сила була силою повітря, тертя незначне. Звичайно, оскільки шайба сповільнюється, а резистивна сила стає меншою, настане момент, коли сила тертя вже не буде незначною порівняно з постійно зменшується опором повітря, так що вищевказані Рівняння більше не точно описують рух. Ми повернемося до цього пункту в підрозділі 3c.