25.6: Закони Кеплера

Закон еліптичної орбіти

I. кожна планета рухається в еліпсі з сонцем в одному фокусі.

Коли енергія негативна$E<0$, і відповідно до Рівняння (25.3.14),

$$\varepsilon=\left(1+\frac{2 E L^{2}}{\mu\left(G m_{1} m_{2}\right)^{2}}\right)^{\frac{1}{2}} \nonumber$$

і ексцентриситет повинен потрапляти в межах діапазону$0 \leq \varepsilon<1$. Ці орбіти є або кола, або еліпси. Зверніть увагу, що закон еліптичної орбіти діє лише в тому випадку, якщо припустити, що діє лише одна центральна сила. Ми ігноруємо гравітаційні взаємодії завдяки всім іншим тілам у Всесвіті, необхідне наближення для нашого аналітичного рішення.

Закон про рівну площу

ІІ. Вектор радіуса від Сонця до планети змітає рівні площі за однаковий час.

Використовуючи аналітичну геометрію в межі малого Δθ, сума площ трикутників на малюнку 25.9 задається

$$\Delta A=\frac{1}{2}(r \Delta \theta) r+\frac{(r \Delta \theta)}{2} \Delta r \nonumber$$

Малюнок 25.9 Закон про рівну площу Кеплера.

Середня швидкість зміни площі$\Delta A$, в часі$\Delta t$, задається

$$\Delta A=\frac{1}{2} \frac{(r \Delta \theta) r}{\Delta t}+\frac{(r \Delta \theta)}{2} \frac{\Delta r}{\Delta t} \nonumber$$

У межі як$\Delta t \rightarrow 0, \Delta \theta \rightarrow 0$, це стає

$$\frac{d A}{d t}=\frac{1}{2} r^{2} \frac{d \theta}{d t} \label{25.5.4}$$

Нагадаємо, що згідно з рівнянням (25.3.7) (відтворюється нижче як Equation\ ref {25.5.5}), кутовий момент часу пов'язаний з$d \theta / d t$ кутовою швидкістю

$$\frac{d \theta}{d t}=\frac{L}{\mu r^{2}} \label{25.5.5}$$

і рівняння\ ref {25.5.4} тоді

$$\frac{d A}{d t}=\frac{L}{2 \mu} \label{25.5.6}$$

Оскільки$L$ і$\mu$ є константами, швидкість зміни площі по відношенню до часу є постійною. Про це часто звично посилається виразом: рівні ділянки змітаються в рівні часи (див. Закони Кеплера на початку цієї глави).

Закон періоду

III. Період обертання T планети навколо Сонця пов'язаний з напіввеликою віссю a еліпса тим,$T^{2}=k a^{3}$ де k однаковий для всіх планет.

Коли Кеплер заявив свій закон періоду для планетарних орбіт на основі спостереження, він лише зазначив залежність від більшої маси Сонця. Оскільки маса Сонця набагато більше маси планет, його спостереження є відмінним наближенням.

Для демонстрації третього закону починаємо з переписування Equation\ ref {25.5.6} у вигляді

$$2 \mu \frac{d A}{d t}=L \label{25.5.7}$$

Рівняння\ ref {25.5.7} можна інтегрувати як

$$\int_{\text {orbit }} 2 \mu d A=\int_{0}^{T} L d t \nonumber$$

де$T$ - період орбіти. Для еліпса,

$$\int_{\text {orbit }}d A=\pi ab \nonumber$$

де$a$ - напіввелика вісь і$b$ - напівмалий вісь (рис. 25.10).

Малюнок 25.10 Напівмалий і напівмалий вісь для еліпса

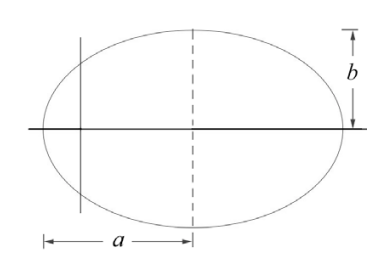
Таким чином, ми маємо

$$T=\frac{2 \mu \pi a b}{L} \label{25.5.10}$$

Квадратне рівняння\ ref {25.5.10} потім дає

$$T^{2}=\frac{4 \pi^{2} \mu^{2} a^{2} b^{2}}{L^{2}} \nonumber$$

У додатку 25B, Рівняння (25.B.20) дає кутовий імпульс через велику піввісь та ексцентриситет. Заміна моменту моменту моменту на рівняння (25.5.11) дає

$$T^{2}=\frac{4 \pi^{2} \mu^{2} a^{2} b^{2}}{\mu G m_{1} m_{2} a\left(1-\varepsilon^{2}\right)} \nonumber$$

У додатку 25B, Рівняння (25.B.17) дає напівмалу вісь, яка при заміщенні на рівняння (25.5.12) дає

$$T^{2}=\frac{4 \pi^{2} \mu^{2} a^{3}}{\mu G m_{1} m_{2}} \nonumber$$

Використовуючи рівняння (25.2.1) для зменшеної маси, квадрат періоду орбіти пропорційний піввеликої осі в кубі,

$$T^{2}=\frac{4 \pi^{2} a^{3}}{G\left(m_{1}+m_{2}\right)} \nonumber$$