25.2: Планетарні орбіти

Зараз ми починаємо дослідження проблеми Кеплера. Визначимо рівняння руху для рухів двох тіл, що взаємодіють через гравітаційну силу (задача двох тіл), використовуючи як силові методи, так і закони збереження.

Зменшення проблеми двох тіл в проблему одного тіла

Почнемо з того, що покажемо, як рух двох тіл, що взаємодіють за допомогою гравітаційної сили (проблема двох тіл), математично еквівалентний руху одного тіла, на яке діє зовнішня центральна гравітаційна сила, де маса єдиного тіла - це зменшена маса$\mu$,

$$\frac{1}{\mu}=\frac{1}{m_{1}}+\frac{1}{m_{2}} \Rightarrow \mu=\frac{m_{1} m_{2}}{m_{1}+m_{2}} \nonumber$$

Після того, як ми вирішимо рух зменшеного тіла в цій еквівалентній проблемі одного тіла, ми можемо повернутися до реальної проблеми двох тіл і вирішити для фактичного руху двох вихідних тіл. Зменшена маса була введена в главі 13 Додаток А цих приміток. Цей додаток використовував подібні, але дещо відмінні від позначення, що використовуються в цьому розділі.

Розглянемо гравітаційну взаємодію двох тіл з масами m і як 1 м2 показано на малюнку 25.1.

Малюнок 25.1 Гравітаційна сила між двома тілами

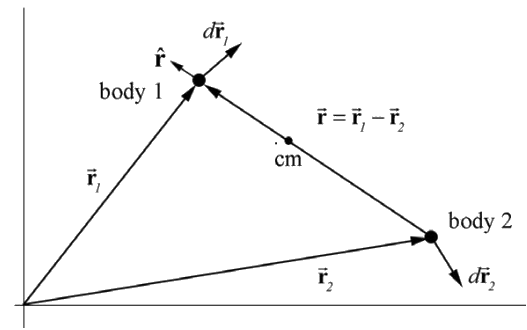
Виберіть систему координат з вибором походження, таку, щоб тіло 1 мало положення,$\overrightarrow{\mathbf{r}}_{1}$ а тіло 2 - положення$\overrightarrow{\mathbf{r}}_{2}$ (рис. 25.2). Вектор відносного положення, що$\overrightarrow{\mathbf{r}}$ вказує від тіла 2 до тіла 1,$\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}_{1}-\overrightarrow{\mathbf{r}}_{2}$ Ми позначаємо величину$\overrightarrow{\mathbf{r}} \text { by }|\overrightarrow{\mathbf{r}}|=r$, де r - відстань між тілами, і$\hat{\mathbf{r}}$ є одиничним вектором, що вказує від тіла 2 до тіла 1, так що$\overrightarrow{\mathbf{r}}=r \hat{\mathbf{r}}$.

Малюнок 25.2 Система координат для задачі двох тіл

Сила на тілі 1 (завдяки взаємодії двох тіл) може бути описана універсальним законом гравітації Ньютона

$$\overrightarrow{\mathbf{F}}_{2,1}=-F_{2,1} \hat{\mathbf{r}}=-G \frac{m_{1} m_{2}}{r^{2}} \hat{\mathbf{r}} \nonumber$$

Нагадаємо, що Третій закон Ньютона вимагає, щоб сила на тіло 2 була рівною за величиною і протилежною в напрямку силі на тілі 1,

$$\overrightarrow{\mathbf{F}}_{1,2}=-\overrightarrow{\mathbf{F}}_{2,1} \nonumber$$

Другий закон Ньютона може застосовуватися індивідуально до двох органів:

\ [\ почати {масив} {l}
\ переправа стрілка {\ mathbf {F}} _ {2,1} =m_ {1}\ frac {d^ {2}\ переправа стрілка {\ mathbf {r}} _ {1}} {d t^ {2}}\\
\ переправа стрілка {\ mathbf {F}} _ {1,2}} =m_ {2}\ frac {d^ {2}\ переправа стрілка {\ mathbf {r}} _ {2}} {d t^ {2}}
\ кінець {масив}\ nonumber\]

Ділення через масу в кожному з рівнянь (25.2.4) і (25.2.5) дає

$$\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}} \nonumber$$

$$\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}} \nonumber$$

Віднімання виразу в рівнянні (25.2.7) з рівняння (25.2.6) дає

$$\frac{\overrightarrow{\mathbf{F}}_{2,1}}{m_{1}}-\frac{\overrightarrow{\mathbf{F}}_{1,2}}{m_{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}_{1}}{d t^{2}}-\frac{d^{2} \overrightarrow{\mathbf{r}}_{2}}{d t^{2}}=\frac{d^{2} \overrightarrow{\mathbf{r}}}{d t^{2}} \nonumber$$

Використовуючи Третій закон Ньютона, рівняння (25.2.3), Рівняння (25.2.8) стає

$$\overrightarrow{\mathbf{F}}_{2,1}\left(\frac{1}{m_{1}}+\frac{1}{m_{2}}\right)=\frac{d^{2} \overrightarrow{\mathbf{r}}}{d t^{2}} \nonumber$$

Використовуючи зменшену масу μ, як визначено в Рівнянні (25.2.1), Рівняння (25.2.9) стає

\ [\ почати {масив} {l}
\ frac {\ переправа стрілка {\ mathbf {F}} _ {2,1}} {\ mu} =\ frac {d^ {2}\ переправа стрілка {\ mathbf {r}}} {d t^ {2}}
\\ переправа {\ mathbf {F}} _ {2,1} =\ му\ frac {d^ {2}\ переправа стрілка {\ mathbf {r}}} {d t^ {2}}
\ кінець {масив}\ nonumber\]

де$\overrightarrow{\mathbf{F}}_{2,1}$ задається рівнянням (25.2.2).

Наш результат має спеціальне тлумачення з використанням Другого закону Ньютона. $\mu$Дозволяти масою одного тіла з$\overrightarrow{\mathbf{r}}=r \hat{\mathbf{r}}$ вектором положення відносно походження O, де$\hat{\mathbf{r}}$ є одиничний вектор, що вказує від початку O до єдиного тіла. Тоді рівняння руху, Рівняння (25.2.10), має на увазі, що єдине тіло маси$\mu$ знаходиться під впливом привабливої гравітаційної сили, що вказує на початок. Отже, початкова гравітаційна задача двох тіл тепер зведена до еквівалентної проблеми одного тіла, яка включає в себе єдине тіло з масою$\mu$ під впливом центральної сили$\overrightarrow{\mathbf{F}}^{G}=-\mathrm{F}_{2,1} \hat{\mathbf{r}}$ Зверніть увагу, що в цій переформулюванні немає тіла, розташованого в центральній точці (походження О). Параметр r у задачі двох тіл - це відносна відстань між початковими двома тілами, тоді як той самий параметр r в задачі одного тіла - це відстань між єдиним тілом і центральною точкою. Це скорочення узагальнює всі центральні сили.