18.4: Опрацьовані приклади

Приклад 18.2 Підвісний стрижень

Рівномірний стрижень довжини$l=2.0 \mathrm{m}$ і маси$m=4.0 \mathrm{kg}$ шарнірно кріпиться до стіни одним кінцем і підвішується до стіни тросом, який кріпиться до іншого кінця стрижня під кутом$\beta=30^{\circ}$ до стрижня (див. Рис. Припустимо, що кабель має нульову масу. Існує контактна сила у шарніра на штоку. Величина і напрямок цієї сили невідомі. Однією з найскладніших частин цих типів проблем є введення кута для сили повороту, а потім вирішити для цього кута, якщо це можливо. У цій задачі ви вирішите за величиною натягу в тросі і напрямком і величиною сили повороту. (а) Що таке напруга в кабелі? (b) Який кут робить сила повороту з балкою? (c) Яка величина сили повороту?

Малюнок 18.7 Приклад 18.2 Малюнок 18.8 Діаграма сили та крутного моменту.

Рішення: а) Діаграма сили показана на малюнку 18.8. Візьміть позитивний$\hat{\mathbf{i}}$ -напрямок, щоб бути праворуч на малюнку вище, і візьміть позитивний$\hat{\mathbf{j}}$ -напрямок, щоб бути вертикально вгору. Сили на стрижень є: гравітаційна сила$m \overrightarrow{\mathbf{g}}=-m g \hat{\mathbf{j}}$, що діє в центрі стрижня; сила, яку трос чинить на стрижень,$\overrightarrow{\mathbf{T}}=T(-\cos \beta \hat{\mathbf{i}}+\sin \beta \hat{\mathbf{j}})$ діючи на правому кінці стрижня; і сила повороту$\overrightarrow{\mathbf{F}}_{\text {pivot }}=F(\cos \alpha \hat{\mathbf{i}}+\sin \alpha \hat{\mathbf{j}})$, що діє при повороті лівого кінця стрижня. Якщо сила$0<\alpha<\pi / 2$ повороту спрямована вгору і вправо на малюнку. Якщо$0>\alpha>-\pi / 2$, сила повороту спрямована вниз і вправо. На даний момент у нас немає підстав очікувати, що це$\alpha$ буде в будь-якому з квадрантів, але це повинно бути в тому чи іншому.

буде в будь-якому з квадрантів, але він повинен бути в тому чи іншому

\ [\ begin {масив} {l}
0=-T\ cos\ бета+F\ cos\ альфа\\
0=-м g+t\ sin\ бета+F\ sin\ альфа
\ кінець {масив}\ nonumber\]

Що стосується точки повороту та приймаючи позитивні крутні моменти проти годинникової стрілки, гравітаційна сила надає негативний крутний момент величини,$m g(l / 2)$ а кабель надає позитивний крутний момент величини$T l \sin \beta$. Сила повороту не надає крутного моменту щодо шкворня. Встановлення суми крутних моментів, рівних нулю, то дає

\ [\ begin {масив} {l}
0=T l\ sin\ бета-м г (л/2)\\
T=\ frac {m g} {2\ sin\ бета}
\ кінець {масив}\ nonumber\]

Цей результат має багато особливостей, які ми очікували б; пропорційний вазі стрижня і обернено пропорційний синусу кута, зробленого кабелем щодо горизонталі. Вставка числових значень дає

$$T=\frac{m g}{2 \sin \beta}=\frac{(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}{2 \sin 30^{\circ}}=39.2 \mathrm{N} \nonumber$$

Існує багато способів знайти кут$\alpha$. Заміна рівняння (18.4.2) для натягу в обидва силові рівняння в Рівнянні (18.4.1) дає

\ [\ begin {масив} {l}
F\ cos\ альфа = t\ cos\ бета = (м г/2)\ cot\ бета\\
F\ sin\ альфа = м г-т\ sin\ бета = м г/2
\ кінець {масив}\ nonumber\]

У Рівнянні (18.4.4), діливши одне рівняння на інше, ми бачимо, що$\tan \alpha=\tan \beta, \alpha=\beta$

Горизонтальні зусилля на штоку повинні скасовуватися. Сила натягу і сила повороту діють з однаковим кутом (але в протилежних горизонтальних напрямках) і, отже, повинні мати однакову величину,

$$F=T=39.2 \mathrm{N} \nonumber$$

Як альтернатива, якби ми не зробили попередніх частин, ми могли б знайти крутний момент щодо точки, де кабель прикріплений до стіни. Кабель не надає крутного моменту щодо цієї точки, а y -компонент сили повороту також не надає крутного моменту. Момент плеча х -складової сили повороту є$l \tan \beta$ і момент плеча ваги l/2. Прирівнювання величин цих двох крутних моментів дає

$$F \cos \alpha l \tan \beta=m g \frac{l}{2} \nonumber$$

еквівалентно першому рівнянню в Рівнянні (18.4.4). Аналогічно, оцінюючи крутний момент щодо правого кінця стрижня, трос не надає крутних моментів, а х -компонент сили повороту не надає крутного моменту. Моментний плече y -складової сили повороту дорівнює l, а моментний плеч ваги - l/2. Прирівнювання величин цих двох крутних моментів дає

$$F \sin \alpha l=m g \frac{l}{2} \nonumber$$

відтворення другого рівняння в Рівнянні (18.4.4). Сенс цього альтернативного рішення полягає в тому, щоб показати, що вибір іншого походження (або навіть більше одного походження) для видалення невідомої сили з рівнянь крутного моменту може дати бажаний результат більш безпосередньо.

Приклад 18.3 Особа, що стоїть на пагорбі

Людина стоїть на пагорбі, який нахилений під$\alpha$ кутом щодо горизонталі (рис. 18.9). Ноги людини розділені на відстань$d$, однією ногою в гору і одним спуском. Центр маси людини знаходиться на відстані$h$ над землею, перпендикулярно схилу пагорба, посередині між ступнями людини. Припустимо, що коефіцієнт статичного тертя між стопами людини і пагорбом досить великий, щоб людина не ковзав. (а) Яка величина нормальної сили на кожній нозі? (b) Наскільки далеко повинні бути один від одного стопи, щоб нормальна сила на верхній стопі була рівною нулю? Це той момент, коли людина починає обертатися і падати.

Малюнок 18.9 Людина, що стоїть на пагорбі Малюнок 18.10 Діаграма сили вільного тіла для людини, що стоїть на пагорбі

Рішення: Діаграма сили на людину показана на малюнку 18.10. Зверніть увагу, що контактні сили були розкладені на компоненти, перпендикулярні і паралельні схилу пагорба. Також показано вибір одиничних векторів та позитивного напрямку крутного моменту. Застосовуючи Другий закон Ньютона до двох складових чистої сили,

$$\hat{\mathbf{j}}: N_{1}+N_{2}-m g \cos \alpha=0 \nonumber$$

$$\hat{\mathbf{i}}: f_{1}+f_{2}-m g \sin \alpha=0 \nonumber$$

Ці два рівняння мають на увазі, що

$$N_{1}+N_{2}=m g \cos \alpha \nonumber$$

$$f_{1}+f_{2}=m g \sin \alpha \nonumber$$

Оцінюючи крутні моменти про центр мас,

$$h\left(f_{1}+f_{2}\right)+\left(N_{2}-N_{1}\right) \frac{d}{2}=0 \nonumber$$

Рівняння (18.4.10) можна переписати як

$$N_{1}-N_{2}=\frac{2 h\left(f_{1}+f_{2}\right)}{d} \nonumber$$

Заміна рівняння (18.4.9) на рівняння (18.4.11) дає

$$N_{1}-N_{2}=\frac{2 h(m g \sin \alpha)}{d} \nonumber$$

Ми можемо вирішити для,$N_{1}$ додавши рівняння (18.4.8) та (18.4.12), а потім діливши на 2, отримуючи

$$N_{1}=\frac{1}{2} m g \cos \alpha+\frac{h(m g \sin \alpha)}{d}=m g\left(\frac{1}{2} \cos \alpha+\frac{h}{d} \sin \alpha\right) \nonumber$$

Аналогічно, ми можемо вирішити для,$N_{2}$ віднімаючи Рівняння (18.4.12) з Рівняння (18.4.8) і діливши на 2, отримуючи

$$N_{2}=m g\left(\frac{1}{2} \cos \alpha-\frac{h}{d} \sin \alpha\right) \nonumber$$

Нормальна сила$N_{2}$, задана в Рівнянні (18.4.14), зникає, коли

$$\frac{1}{2} \cos \alpha=\frac{h}{d} \sin \alpha \nonumber$$

які можна вирішити за мінімальну відстань між ніжками,

$$d=2 h(\tan \alpha) \nonumber$$

Слід зазначити, що жодної конкретної моделі сили тертя не використовувалося, тобто в задачу не увійшов жоден коефіцієнт статичного тертя. Дві сили тертя і не$f_{2}$ були$f_{1}$ визначені окремо; тільки їх сума увійшла в наведені вище розрахунки.

Приклад 18.4 Коліно

Чоловік масою m = 70 кг ось-ось почне забіг. Припустимо, вага бігуна рівномірно розподілений на обидві ноги. Зв'язка надколінка в коліні прикріплюється до верхньої великогомілкової кістки і проходить над колінної чашечкою. При згинанні коліна сила розтягування$\overrightarrow{\mathbf{T}}$, яку зв'язка чинить на верхню великогомілкову кістку, направляється під$\theta=40^{\circ}$ кутом щодо горизонталі. Стегнова кістка надає силу$\overrightarrow{\mathbf{F}}$ на верхню великогомілкову кістку. Кут,$\alpha$ який ця сила робить з вертикаллю, буде змінюватися і є одним з невідомих для вирішення. Припустимо, що зв'язка з'єднана на відстані$d=3.8 \mathrm{cm}$, безпосередньо нижче точки контакту стегнової кістки на великогомілкової кістки. Точка контакту стопи і землі - це відстань$s=3.6 \times 10^{1} \mathrm{cm}$ від вертикальної лінії, що проходить через точку контакту стегнової кістки на великогомілкової кістки. Центр маси гомілки лежить на відстані$x=1.8 \times 10^{1} \mathrm{cm}$ від цієї ж вертикальної лінії. Припустимо, маса$m_{\mathrm{L}}$ гомілки становить 1/10 від маси тіла (рис. 18.11). (а) Знайти величину T сили$\overrightarrow{\mathbf{T}}$ зв'язки надколінка на великогомілкової кістки. (б) Знайти напрямок (кут α) сили$\overrightarrow{\mathbf{F}}$ стегнової кістки на великогомілкової кістки. (в) Знайти величину F сили$\overrightarrow{\mathbf{F}}$ стегнової кістки на великогомілкової кістки.

Малюнок 18.11 Приклад 18.4 Рисунок 18.12 Діаграма сили крутного моменту для коліна

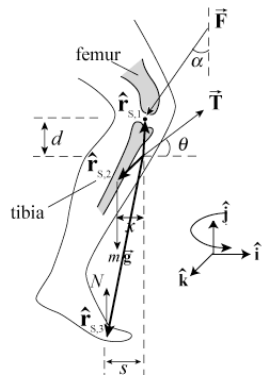
Рішення: а) Виберіть вектор$\hat{\mathbf{i}}$ одиниці, який буде спрямований горизонтально вправо і$\hat{\mathbf{j}}$ спрямований вертикально вгору. Перша умова для статичної рівноваги, Рівняння (18.1.1), що сума сил дорівнює нулю стає

$$\hat{\mathbf{i}}:-F \sin \alpha+T \cos \theta=0 \nonumber$$

$$\hat{\mathbf{j}}: N-F \cos \alpha+T \sin \theta-(1 / 10) m g=0 \nonumber$$

Оскільки вага рівномірно розподіляється на дві ноги, нормальна сила на одній нозі дорівнює половині ваги, або

$$N=(1 / 2) m g \nonumber$$

Рівняння (18.4.18) стає

\ [\ почати {масив} {r}
\ hat {\ mathbf {j}} :( 1/2) м г-ф\ cos\ альфа+т\ син\ тета- (1/10) м г = 0\\
(2/5) м г-ф\ cos\ альфа+t\ sin\ theta = 0
\ кінець {масив}\ nonumber\]

Схема крутного моменту - сила на коліні показана на малюнку 18.12. Виберіть точку дії зв'язки на великогомілкової кістки як точку,$S$ про яку слід обчислити крутні моменти. Зверніть увагу, що сила розтягування,$\overrightarrow{\mathbf{T}}$ яку зв'язка чинить на верхню великогомілкову кістку, не зробить ніякого внеску в крутний момент щодо цієї точки$S$. Це може трохи допомогти при проведенні розрахунків. Виберіть проти годинникової стрілки як позитивний напрямок для крутного моменту; це позитивне$\hat{\mathbf{k}}$ - напрямок. Тоді крутний момент за рахунок сили$\overrightarrow{\mathbf{F}}$ стегнової кістки на великогомілкової кістки дорівнює

$$\vec{\tau}_{S, 1}=\overrightarrow{\mathbf{r}}_{S, 1} \times \overrightarrow{\mathbf{F}}=d \hat{\mathbf{j}} \times(-F \sin \alpha \hat{\mathbf{i}}-F \cos \alpha \hat{\mathbf{j}})=d F \sin \alpha \hat{\mathbf{k}} \nonumber$$

Крутний момент, обумовлений масою ноги, становить

$$\vec{\tau}_{S, 2}=\overrightarrow{\mathbf{r}}_{S, 2} \times(-m g / 10) \hat{\mathbf{j}}=\left(-x \hat{\mathbf{i}}-y_{L} \hat{\mathbf{j}}\right) \times(-m g / 10) \hat{\mathbf{j}}=(1 / 10) x m g \hat{\mathbf{k}} \nonumber$$

Крутний момент, обумовлений нормальною силою грунту, дорівнює

$$\vec{\tau}_{S, 3}=\overrightarrow{\mathbf{r}}_{S, 3} \times N \hat{\mathbf{j}}=\left(-s \hat{\mathbf{i}}-y_{N} \hat{\mathbf{j}}\right) \times N \hat{\mathbf{j}}=-s N \hat{\mathbf{k}}=-(1 / 2) s m g \hat{\mathbf{k}} \nonumber$$

(У рівняннях (18.4.22) і (18.4.23)$y_{L} \text { and } y_{N}$ є вертикальними зміщеннями τ точки, де вага ноги і нормальна сила по відношенню до точки S; як видно, ці величини не входять безпосередньо в розрахунки.) Умова, що сума крутних моментів навколо точки$S$ зникає, Рівняння (18.1.2),

$$\vec{\tau}_{S, \text { total }}=\vec{\tau}_{S, 1}+\vec{\tau}_{S, 2}+\vec{\tau}_{S, 3}=\overrightarrow{0} \nonumber$$

стає

$$d F \sin \alpha \hat{\mathbf{k}}+(1 / 10) x m g \hat{\mathbf{k}}-(1 / 2) s m g \hat{\mathbf{k}}=\overrightarrow{\boldsymbol{0}} \nonumber$$

Три рівняння в трьох невідомих підсумовуються нижче:

\ [\ почати {масив} {r}
-F\ sin\ альфа+т\ cos\ тета = 0\\\
(2/5) м г-ф\ cos\ альфа+т\ sin\ тета = 0\\
d F\ sin\ альфа+ (1/10) х м г- (1/2) s m g = 0
\ кінець {масив}\ nonumber\]

Рівняння горизонтальної сили, перше в (18.4.26), означає, що

$$F \sin \alpha=T \cos \theta \nonumber$$

Підставляючи це в рівняння крутного моменту, третє рівняння (18.4.26), дає

$$d T \cos \theta+(1 / 10) x m g-s(1 / 2) m g=0 \nonumber$$

Зверніть увагу, що Рівняння (18.4.28) - це рівняння, яке було б отримано, якби ми вибрали точку контакту між великогомілкової кістки та стегнової кістки як точку, про яку слід визначити крутний момент. Якби ми вибрали цей пункт, ми б врятували один незначний алгебраїчний крок. Ми можемо вирішити це рівняння (18.4.28) для величини T сили$\overrightarrow{\mathbf{T}}$ зв'язки надколінка на великогомілкової кістки,

$$T=\frac{s(1 / 2) m g-(1 / 10) x m g}{d \cos \theta} \nonumber$$

Вставка числових значень у рівняння (18.4.29),

\ [\ почати {вирівняний}
T & =( 70\ mathrm {кг})\ ліворуч (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ праворуч)\ frac {\ ліворуч (3,6\ раз 10^ {1}\ mathrm {m}\ праворуч) (1/2) - (1/10)\ ліворуч (1.8\ раз 10^ {}\ mathrm {m}\ праворуч)} {\ ліворуч (3.8\ раз 10^ {-2}\ mathrm {m}\ праворуч)\ cos\ ліворуч (40^ {\ circ}\ праворуч)}\\
&=3. 8\ раз 10^ {3}\ mathrm {N}
\ кінець {вирівняний}\ номер\]

б) Тепер ми можемо вирішити напрямок$\alpha$ сили$\overrightarrow{\mathbf{F}}$ стегнової кістки на великогомілкової кістки наступним чином. Перепишіть два рівняння сили в (18.4.26) як

\ [\ begin {масив} {l}
F\ cos\ альфа = (2/5) м g+t\ sin\ тета\\
F\ sin\ альфа = t\ cos\ тета
\ кінець {масив}\ nonumber\]

Ділення цих рівнянь дає

$$\frac{F \cos \alpha}{F \sin \alpha}=\operatorname{cotan} \alpha=\frac{(2 / 5) m g+T \sin \theta}{T \cos \theta} \nonumber$$

І так

\ [\ почати {масив} {l}
\ альфа =\ ім'я оператора {cotan} ^ {-1}\ лівий (\ frac {(2/5) m g+t\ sin\ тета} {T\ cos\ тета}\ праворуч)\\ альфа =
\ ім'я оператора {cotan} ^ {-1}\ лівий (\ frac {(2/5) (70\ mathrm {kg})\ ліворуч (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ праворуч) +\ ліворуч (3.4\ times 10^ {3}\ mathrm {N}\ праворуч)\ sin\ ліворуч (40^ {\ circ}\ праворуч)} {\ ліворуч (3.4\ раз 10^ {3}\ mathrm {N}\ праворуч)\ cos\ ліворуч (40^ {\ circ}\ праворуч)}\ праворуч) =47^ {\ circ}
\ кінець {масив}\ nonumber\]

в) Тепер ми можемо використовувати горизонтальне рівняння сили для обчислення величини F сили стегнової кістки$\overrightarrow{\mathbf{F}}$ на великогомілкової кістки з Рівняння (18.4.27),

$$F=\frac{\left(3.8 \times 10^{3} \mathrm{N}\right) \cos \left(40^{\circ}\right)}{\sin \left(47^{\circ}\right)}=4.0 \times 10^{3} \mathrm{N} \nonumber$$

Зверніть увагу, ви можете знайти символічний вираз для$\alpha$ того, щоб не передбачалося проміжний числовий розрахунок натягу. Це досить складно алгебраїчно; в основному, останні два рівняння в (18.4.26) вирішуються для F і T з точки зору$\alpha, \theta$ та інших змінних (пропонується Правило Крамера), а результати підставляються в перше з (18.4.26). Отриманий вираз

\ [\ почати {вирівняний}
\ кот\ альфа &=\ розрив {(s/2-х/10)\ sin\ ліворуч (40^ {\ circ}\ праворуч) +\ ліворуч ((2 d/5)\ cos\ ліворуч (40^ {\ circ}\ праворуч)} {(s/2-х/10)\ cos\ ліворуч (40^ {\ circ}\ праворуч)} {(s/2-х/10)\ cos\ ліворуч (40^ {\ circ}\ праворуч)}\\
&=\ tan\ ліворуч (40^ {\ circ}\ праворуч) +\ розрив {2 d/5} {s/2-x/10}
\ кінець {вирівняний}\ номер\]

що призводить до того ж числового результату,$\alpha=47^{\circ}$