18.3: Узагальнений закон важеля

Ми можемо продовжити Закон важеля на випадок, коли дві\(\overrightarrow{\mathbf{F}}_{1} \text { and } \overrightarrow{\mathbf{F}}_{2}\) зовнішні сили діють на поворотну балку під\(\theta_{1} \text { and } \theta_{2}\) кутами щодо горизонталі, як показано на малюнку 18.4. Протягом усього цього обговорення кути будуть обмежені діапазоном\(\left[0 \leq \theta_{1}, \theta_{2} \leq \pi\right]\). Знову нехтуємо товщиною балки і візьмемо точку повороту, щоб бути центром маси.

Малюнок 18.4 Сили, що діють під кутами до поворотної балки.

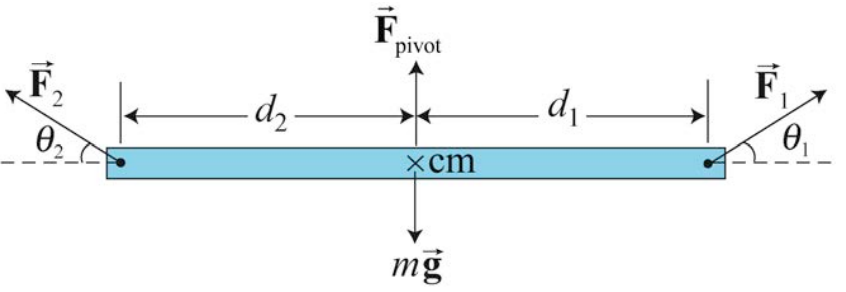
Сили\(\overrightarrow{\mathbf{F}}_{1} \text { and } \overrightarrow{\mathbf{F}}_{2}\) можуть бути розкладені на окремі векторні складові відповідно\(\left(\overrightarrow{\mathbf{F}}_{1, \|}, \overrightarrow{\mathbf{F}}_{1, \perp}\right) \text { and }\left(\overrightarrow{\mathbf{F}}_{2, \|}, \overrightarrow{\mathbf{F}}_{2, \perp}\right)\), де\(\overrightarrow{\mathbf{F}}_{1, \|} \text { and } \overrightarrow{\mathbf{F}}_{2, \|}\) розташовані горизонтальні векторні проекції двох сил щодо напрямку, утвореного довжиною променя,\(\overrightarrow{\mathbf{F}}_{1, \perp}\) і\(\overrightarrow{\mathbf{F}}_{2, \perp}\) є перпендикулярними векторними проекціями. відповідно до балки (рис. 18.5), з

\[\overrightarrow{\mathbf{F}}_{1}=\overrightarrow{\mathbf{F}}_{1, \|}+\overrightarrow{\mathbf{F}}_{1, \perp} \nonumber \]

\[\overrightarrow{\mathbf{F}}_{2}=\overrightarrow{\mathbf{F}}_{2, \|}+\overrightarrow{\mathbf{F}}_{2, \perp} \nonumber \]

Малюнок 18.5 Векторне розкладання сил.

Горизонтальними складовими сил є

\[F_{1, \|}=F_{1} \cos \theta_{1} \nonumber \]

\[F_{2, \|}=-F_{2} \cos \theta_{2} \nonumber \]

де наш вибір позитивного горизонтального напрямку знаходиться праворуч. Жодна горизонтальна складова сили не сприяє можливому обертальному руху балки. Сума цих горизонтальних сил повинна дорівнювати нулю,

\[F_{1} \cos \theta_{1}-F_{2} \cos \theta_{2}=0 \nonumber \]

Перпендикулярні складові сили

\[F_{1, \perp}=F_{1} \sin \theta_{1} \nonumber \]

\[F_{2, \perp}=F_{2} \sin \theta_{2} \nonumber \]

де позитивний вертикальний напрямок - вгору. Перпендикулярні складові сил також повинні дорівнювати нулю,

\[F_{\text {pivot }}-m_{b} g+F_{1} \sin \theta_{1}+F_{2} \sin \theta_{2}=0 \nonumber \]

У законі\(F_{1, \perp} \text { and } F_{2, \perp}\) важеля беруть участь лише вертикальні складові зовнішніх сил (але горизонтальні складові повинні врівноважувати, як в Рівнянні (18.3.5), для рівноваги). Тоді Закон важеля можна продовжити наступним чином.

Узагальнений закон важеля Промінь довжиною l врівноважується на точці повороту, яка розміщена безпосередньо під центром маси балки. Припустимо, сила\(\overrightarrow{\mathbf{F}}_{1}\) діє на балку\(d_{1}\) на відстань праворуч від точки повороту. Друга сила\(\overrightarrow{\mathbf{F}}_{2}\) діє на балку\(d_{2}\) на відстань зліва від точки повороту. Балка залишиться в статичній рівновазі, якщо будуть виконані наступні дві умови:

1) Сумарна сила на балці дорівнює нулю,

2) Твір величини перпендикулярної складової сили з відстанню до шарніра однаково для кожної сили,

\[d_{1}\left|F_{1, \perp}\right|=d_{2}\left|F_{2, \perp}\right| \nonumber \]

Узагальнений закон важеля може бути викладений в еквівалентній формі,

\[d_{1} F_{1} \sin \theta_{1}=d_{2} F_{2} \sin \theta_{2} \nonumber \]

Тепер ми покажемо, що узагальнений закон важеля можна переосмислити як твердження про те, що векторна сума крутних моментів навколо точки повороту\(S\) дорівнює нулю, коли на наш промінь\(\overrightarrow{\mathbf{F}}_{1} \text { and } \overrightarrow{\mathbf{F}}_{2}\) діють лише дві сили, як показано на малюнку 18.6.

Малюнок 18.6 Діаграма сили і крутного моменту.

Давайте виберемо позитивний z -напрямок, щоб вказати з площини сторінки, тоді крутний момент, що вказує на сторінку, матиме позитивний z -компонент крутного моменту (обертання проти годинникової стрілки позитивні). З нашого визначення крутного моменту навколо точки повороту величина крутного моменту, обумовленого силою\(\overrightarrow{\mathbf{F}}_{1}\), задається

\[\tau_{S, 1}=d_{1} F_{1} \sin \theta_{1} \nonumber \]

З правилом правої руки це поза сторінкою (в напрямку проти годинникової стрілки), тому складова крутного моменту позитивна, отже,

\[\left(\tau_{S, 1}\right)_{z}=d_{1} F_{1} \sin \theta_{1} \nonumber \]

Крутний момент, обумовлений\(\overrightarrow{\mathbf{F}}_{2}\) приблизно точкою повороту, знаходиться на сторінці (напрямок за годинниковою стрілкою), а складова крутного моменту є негативною і задається

\[\left(\tau_{S, 2}\right)_{z}=-d_{2} F_{2} \sin \theta_{2} \nonumber \]

z -складова крутного моменту являє собою суму z -складових окремих крутних моментів і дорівнює нулю,

\[\left(\tau_{S, \text { total }}\right)_{z}=\left(\tau_{S, 1}\right)_{z}+\left(\tau_{S, 2}\right)_{z}=d_{1} F_{1} \sin \theta_{1}-d_{2} F_{2} \sin \theta_{2}=0 \nonumber \]

що еквівалентно узагальненому закону важеля, рівняння (18.3.10),

\[d_{1} F_{1} \sin \theta_{1}=d_{2} F_{2} \sin \theta_{2} \nonumber \]