23.2: Дорога до хаосу
Рівняння руху
Для веденого маятника природною мірою рушійної сили є його відношення до вагиmg, Тейлор називає це силою приводу, тому для рушійної сили
F(t)=F0cosωt,
сила приводуγ визначається
γ=F0/mg.
Рівняння руху (з резистивною силою демпфування−bv і, отже, резистивним крутним моментом−bL2˙ϕ) таке:
mL2¨ϕ=−bL2˙ϕ−mgLsinϕ+LF(t)
Діливши наmL2 і записуючиb/m=2β демпфуючий член (щоб збігатися з позначенням Тейлора, його рівняння 12.12) отримаємо (зω20=g/L)
¨ϕ+2β˙ϕ+ω20sinϕ=γω20cosωt.
Поведінка на поступове збільшення рушійної сили: період подвоєння
γ=F0/mgРушійною силою є безрозмірне відношення сили приводу до ваги, тому якщо це мало, маятник не буде приведений до великих амплітуд, і справді ми виявляємо, що після початкових перехідних процесів він осідає на рух на водінній частоті, близькій до лінеаризованого випадку. Ми очікуємо, що речі ускладнюватимуться, коли коливання мають амплітуду порядку радіан, що означає рушійну силу, порівнянну з вагою. І дійсно вони роблять.
Тут ми покажемо, що наш аплет відтворює послідовність, знайдену Тейлором, коли сила руху збільшується.
У рівнянні руху
¨ϕ+2β˙ϕ+ω20sinϕ=γω20cosωt,
Тому ми вибираємо його цінностіω0=1.5,2β=0.75,ω=1 і поступово0.9 збільшуємосяγ від того1.0829, де починається хаос.

Дляγ=0.9, (див. Малюнок) коливання (після коротких початкових перехідних процесів) виглядає як синусоїда, хоча вона трохи плоска, і зверніть увагу, що амплітуда (бірюза в коробці) більшеπ/2, ніж, позитивні і негативні коливання рівні за величиною до п'яти цифр точності після п'яти або близько того коливання.
Ви можете переконатися в цьому самі, відкривши аплет! Клацніть тут. Аплет відображає графік і одночасно показує маятник, що розгойдується (панель клацання вгорі праворуч).
Боγ=1.06, є більший початковий перехідний, віддалено нагадує трицикл, який ми зустрінемося найближчим часом. Насправді це можна придушити, починаючи зφ=−π/2 (нижній повзунок праворуч), але все ще є перехідні процеси: піки не рівномірні до п'ятизначної точності приблизно до сорока циклів.
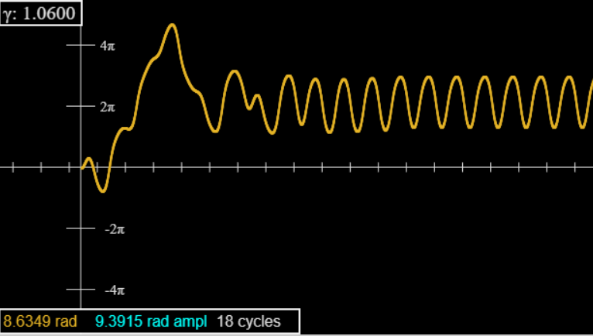
Боγ=1.0662, є дуже довгі перехідні процеси: не видно при погляді на графік (на аплеті), але виявляється шляхом моніторингу зчитування амплітуди (бірюзові цифри в коробці на графіку), значення на останньому екстремумі.
Щоб пройти повз цих перехідних процесів, встановіть швидкість аплету на 50 (це не впливає на точність, лише друкує набагато менше точок). Виконайте 350 циклів, потім зробіть паузу і перейдіть до швидкості = 2. Ви побачите, що піки тепер чергуються по висоті до показаної п'ятизначної точності, виглядає як подвоєння періоду - але це не так, запустіть кілька тисяч циклів, якщо у вас є терпіння, і ви виявите, що всі вершини мають однакову висоту. Це був давно прожитий минущий попередник періоду подвоєння переходу.
Перейшовши до 1.0664, ви побачите як піки, так і падіння, які зараз чергуються за амплітудою, протягом чітко визначеного періоду 2, який триває до 1.0792. (Подивіться на 1.075 після 70 або близько того циклів - і встановіть початковий кут на -90.)
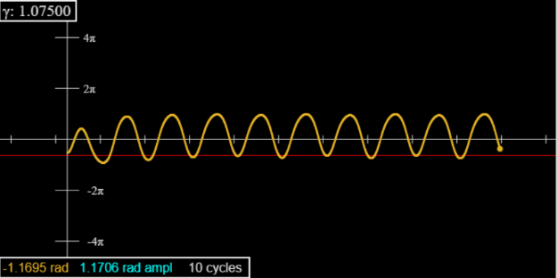
Використовуйте повзунок «Червона лінія» трохи нижче графіка, щоб перевірити висоту послідовних піків або провалів.
Боγ=1.0793, період знову подвоюється: послідовні піки тепер порядку 0,4 радіани один від одного, але послідовні «високі» піки раптово приблизно 0,01 радіана один від одного. (Щоб побачити їх краще на аплеті, збільште вертикальний масштаб і перемістіть червону лінію.)
Боγ=1.0821 є подальше подвоєння до циклу 8, потім на 1.0827 до циклу 16.
Подивіться на графік 1.0826: зокрема, слабо червона горизонтальна лінія біля низу. Кожен четвертий провал йде нижче лінії, але наступні найнижчі провали чергуються між дотиком до лінії і не зовсім доходячи до неї. Це 8 цикл.

Відомо, що інтервали між послідовними подвоєннями зменшуються в разиδ=4.6692, виявлені повсюдно в період подвоєння каскадів, і називаються числом Фейгенбаума, після його першовідкривача. Наша п'ятизначна точність занадто груба, щоб слідувати цій послідовності далі, але ми можемо встановити (або принаймні зробити дуже правдоподібним!) що за межі геометричних рядів приγc=1.0829 періодичності зникає (тимчасово, як ми побачимо), система хаотична. (Звичайно, значенняγ залежать від обраного параметра демпфування і т.д., універсальним є тільки співвідношення подвоєння інтервалів.)

Насправді повна картина складна: є подальші інтервали періодичності, наприклад 6 цикл вγ=1.0845, зображений тут.
Різні атрактори
Описані вище періодичні рішення називаються «атрактори»: конфігурації, де система осідає після того, як спочатку блукає навколо.
Очевидно, що атрактори змінюються з силою руху, менш очевидно, що вони можуть бути різними для різних початкових умов. Тейлор показує, що дляγ=1.077 прийомуφ(0)=0 дає 3-цикл після перехідних процесів, алеφ(0)=−π/2 дає 2-цикл. (Легко перевіряється за допомогою аплету!)
Дивлячись на початкові мандри, які можуть бути зовсім іншими при дуже невеликих змінях сили руху (порівняйте 1.0730 з 1.0729 і 1.0731, використовуйте швидкість 5, це не впливає на точність). Але ви можете бачити, що ці початкові мандри включають елементи з обох атракторів.
Вправа: використовуйте наступний аплет для побудови одночасно 1.0729 і 1.0730, всі інші параметри однакові, швидкість 5.
Вправа: Використовуйте аплет, щоб знайти під яким кутом відбувається перехід від одного атрактора до іншого. І вивчіть, що відбувається в діапазоні сильних сторін руху.
Це найпростіші атрактори: є куди більш складні сутності, звані дивними атракторами, ми поговоримо пізніше.
Вправи: Спробуйте різні значення константи демпфування і подивіться, як це впливає на послідовність біфуркації.
Чутливість до початкових умов
Нагадаємо, що для лінійного демпфірованого керованого осцилятора, який можна точно вирішити, ми виявили, що зміна початкових умов змінювала шлях, звичайно, але різниця між шляхами загасала в геометричній прогресії: криві зійшлися.
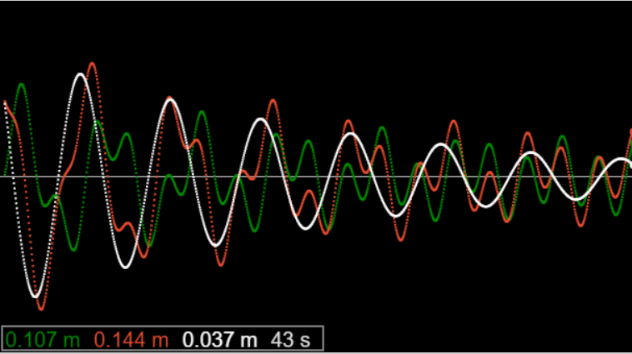
Ця ілюстрація взята з більш раннього аплету: червона та зелена криві відповідають різним початковим умовам, біла крива - це різниця між ними, очевидно, експоненціально зменшується, що можна перевірити аналітично.
Для демпфірованого веденого маятника картина складніша. Дляγ<γc=1.0829 кривих, що відповідають дещо іншим початковим умовам, будуть сходитися (за винятком, наприклад,γ=1.077 де, як говорилося вище, змінюючи початковий кут в певній точці перемикачі утворюють кінцевий тритактний на двотактний).
Показник Ляпунова
Боγ>γc, криві навіть з дуже малими початковими відмінностями (скажімо,10−4 радіани) відокремлюються експоненціально, як eλt,λназивається показник Ляпунова.
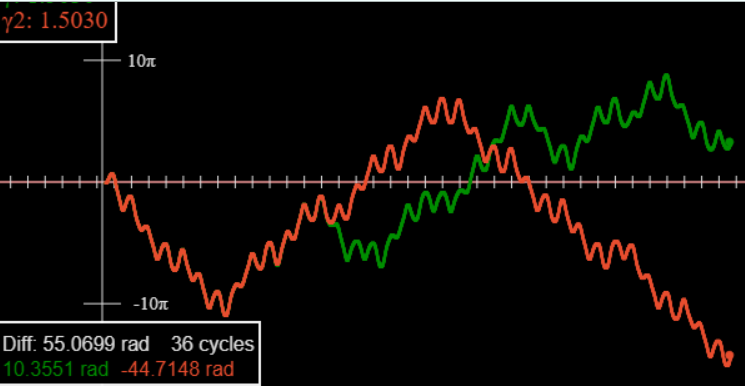
Майте на увазі, однак, що це хаотичний рух, розбіжність не така плавна, як зближення, зображене вище для лінійної системи. Цей графік взято з нашого двоколійного аплету.
Проте, (середню) експоненціальну природу можна розрізнити шляхом побудови логарифма різниці від часу:

Це з нашого аплету різниці журналу. Це дуже близько до рис Тейлора 12.13. Червона лінія нахилу дає показник Ляпунова.
(Червона лінія має регульоване положення та нахил.)
Побудова швидкості проти часу
Як обговорювалося в Тейлорі, подальше збільшення рушійної сили поза хаотичним порогом може призвести до коротких нехаотичних інтервалів, таких як той, що містить шість циклів на 1.0845, проілюстрований вище, але є два довгі відрізки нехаотичної поведінки в діапазоні параметрів Тейлора, від 1.1098 до 1.1482 і від від 1,3 до 1,48.
У більш сильному діапазоні рушійних сил маятник рухається повністю навколо в кожному циклі, тому побудова положення проти часу дає «округлі сходи» вид графіка. Перевірте це за допомогою аплету.

Рішення полягає в тому, щоб побудувати швидкість від часу, і тим самим виявити, що відбувається повторення періоду подвоєння шляху до хаосу у верхньому кінці цього інтервалу. Клацніть дляdϕ/dt побудови графіка замістьϕ.
Державні космічні траєкторії
Це може бути освітлюючим спостерігати, як рух розвивається в часі в двовимірному просторі стану (ϕ,˙ϕ). (Так само називається фазовим простором.) Дивіться аплет Державного простору!
Тепер для частинки в незалежному від часу потенціалі, вказуючи положення і швидкість в даний момент визначає майбутній шлях, але це не так, прискорення визначається фазою рушійної сили, яка змінюється в часі, тому система дійсно потрібні три параметри, щоб задати його подальший рух.
Це означає, що фазовий простір дійсно тривимірний, третій напрямок - це рушійна фаза, або, що еквівалентно, час, але періодичний з періодом рушійної сили. У цьому тривимірному просторі шляхи не можуть перетинатися, в будь-який момент майбутній шлях однозначно визначається. Наші двовимірні ділянки є проекціями цих тривимірних шляхів на площину (ϕ,˙ϕ).
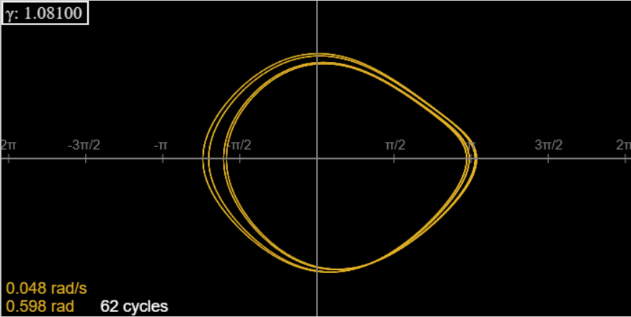
Ось 4-цикл наγ=1.081, мінус перші 20 циклів, для усунення перехідних процесів.
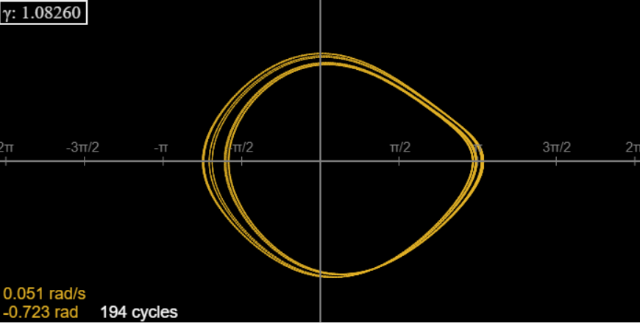
Дляγ=1.0826, існує 8-цикл. Запустіть аплет протягом 40 циклів або близько того, щоб позбутися від перехідних процесів, а потім подивіться на крайній лівий кінець кривої, породженої запуском, скажімо, до 200 циклів. Це не схоже на те, що є 8 ліній, але зовнішня лінія і дві внутрішні лінії подвоюються (зверніть увагу на товщину). Ви можете перевірити це за допомогою аплету, зробивши паузу на осі і помітивши зчитування позиції: є 8 різних значень, які повторюються. (Вам не потрібно зупинятися прямо на осі - ви можете зупинитися близько до неї, а потім скористатися кроковими кнопками, щоб дістатися туди.)
Бо шлях хаотичний - але не виглядає занадто різним у цьому масштабі!γ=1.0830 Перевірте це за допомогою аплету. Хаос стає більш очевидним при подальшому зростанніγ. γ=1.087Бо візерунок «відгодовують», так як повторювані цикли відрізняються незначно.

Для подальшого збільшенняγ, орбітальний рух охоплює більшу територію: вγ=1.1, ось перші триста або близько того циклів.
Поклавши багато орбіт на високій швидкості, ми знаходимо:

Однак тут історія ускладнюється: виявляється, що ця хаотична серія орбіт насправді є перехідною, і приблизно через 300 циклів система переходить на 3-цикл, де вона залишається. Насправді ми досягли діапазонуγ (приблизно 1.1098 до 1.1482), де після початкових перехідних процесів (які можуть бути досить довгими) рух не хаотичний, а 3-тактний.
Очевидно, що для цієї системи є багато чого вивчити! Щоб краще зрозуміти ці складнощі, ми спробуємо інший підхід, розроблений Пуанкаре.
Розділи Пуанкаре
Дивлячись на наведені вище зображення, коли ми переходимо від однієї орбіти до послідовних подвійних періодів, а потім хаосу, загальна форма орбіти не змінюється різко (до цього остаточного трициклового). Цікавими речами є подвоєння послідовності, хаос і атрактори - можливо, ми будуємо занадто багато інформації.
Щоб зосередитись на тому, що важливо, Пуанкаре побудував одну точку з кожного циклу, тепер це називається секцією Пуанкаре. Щоб побудувати це, починаємо зt=0 позиції, маркуємо їїP0=(φ0,˙φ0). Потім додайте точкуP1=(φ1,˙φ1) точно на один цикл пізніше, і так далі—вказує один цикл один від одногоP2=(φ2,˙φ2), тощо Тепер, знаючи положенняP=(φ,˙φ) в просторі стану, недостатньо інформації для побудови майбутньої орбіти - нам також потрібно знати фазу рушійної сили. Але шляхом побудови точок один цикл в часі один від одного, вони всі побачать ту саму фазу стартової сили, тому трансформація, яка веде нас відP0 до,P1 просто повторюється в переході відP1 до іP2 т.д.
Щоб побачити ці окремі точки в аплеті State Space, натисніть «Показати червону крапку»: під час запуску аплет покаже одну крапку за цикл червоною.
Миттєво думаючи про повний тривимірний фазовий простір, перетин Пуанкаре - це поперечний переріз на початковій фазі циклу водіння. Ми додали до аплету параметр фази червоної точки, щоб знайти розділ Пуанкаре на іншій фазі. Роблячи це кілька разів, і дивлячись на рух червоних крапок, дає більш повну картину руху.
Таким чином, розділ Пуанкаре, при збільшенніγ через послідовність подвоєння (і завжди опускаючи початкові перехідні процеси) переходить від однієї точки до двох точок, до чотирьох тощо.
Щоб побачити все це трохи чіткіше, наступний аплет, який називається Poincaré Section, показує лише одну крапку за цикл, але має опцію фази, щоб ви могли дивитися на будь-який етап циклу.
Вправа: перевірте все це за допомогою аплету Poincaré! Щоб добре це побачити, натисніть Переключити початк/Масштаб, скористайтеся повзунками, щоб відцентрувати візерунок, більш-менш, а потім масштабуйте його. Виконайте кілька сотень циклів, а потім натисніть «Приховати трасування», а потім «Показати трасування», щоб позбутися від перехідних процесів.
Почніть зγ=1.0826. Розділ Пуанкаре - це вісім точок на кривій, на 1.0827 ви можете розрізнити 16. До 1.0829 ми маємо хаос, і розділ має кінцеві розтяжки кривої, а не тільки точки. Це виглядає дуже схоже на 1.0831, але - сюрприз - на 1.0830 це набір точок (32?) деякі подвоїлися. Це говорить нам про те, що ми знаходимося в мінному полі. У хаосі немає нічого гладкого.
Окрім перерв, у міруγ збільшення, розділ Пуанкаре заповнює криву, яка потім еволюціонує до дивного атрактора, показаного Тейлором та іншими. Переходячи з 1.090 кроком до 1.095, крива розвивається на другу, тісно паралельну, гілку. При 1.09650 дві гілки рівні по довжині, потім на 1.097 нижня гілка раптом подовжує довгу криву, виглядає набагато однаково на 1.100, потім на 1,15 дізнаємося виникнення дивного атрактора.
Але насправді це спрощена розповідь: бувають перебої. Наприклад, наγ=1.0960 5-ти циклі, немає хаосу (він зникає при зміні на 0.0001). І в 1.12 ми знаходимося в інтервалі 3-цикл згаданий раніше.
Так чи інакше, дивний атрактор продовжує з'являтися знову, і в 1,5 він виглядає так:

Це виглядає досить тонким порівняно з картиною Тейлора для того жγ: причина в тому, що ми зберегли сильне демпфування.
Змінюючись на2β=0.375, відновлюємо картину Тейлора. Як і він, ми показуємо тут (з аплету) атрактор і послідовні збільшення однієї частини, щоб дати якийсь натяк на фрактальну структуру:

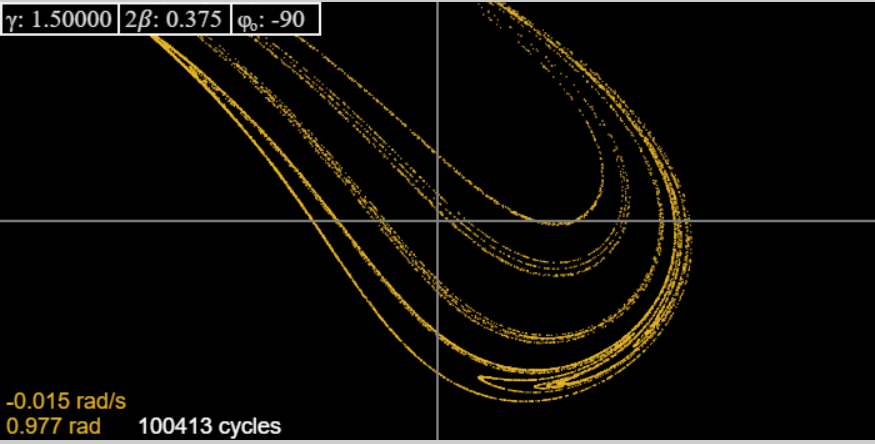
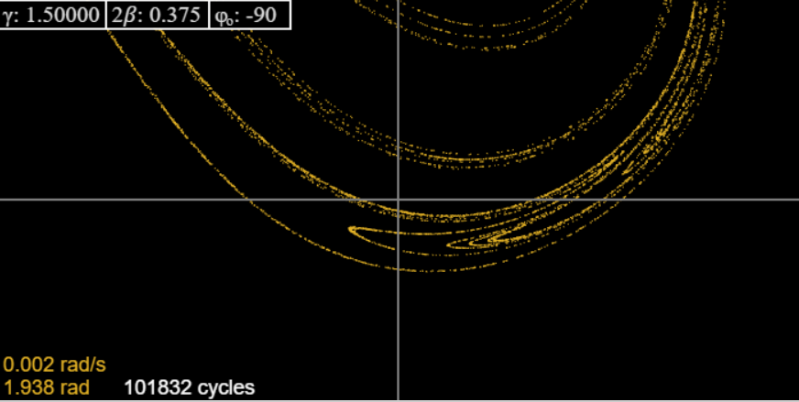
Ми повинні визнати, що при найбільшому збільшенні картина Тейлора, безумовно, перевершує ту, що генерується аплетом, але не суперечить їй - насправді це заспокоює нас, що аплет надійний до рівня визначення, який є очевидним при погляді на нього.
Вправа: Використовуйте останні два аплети для вивчення інших областей простору параметрів. Що відбувається при зміні демпфування? Перехід від2β=0.375 до2β=0.75 атрактора має ту ж загальну форму, але набагато вужче. Потім перейдіть у кроці 0.001 до 0.76. Для одних значень ви бачите атрактор, а для інших - цикл, різної довжини. Існує двотактний від 0,76 до 0,766, потім чотиритактний, потім на 0,78 назад в двотактний, при 0,814 - однотактний. Якщо підняти силу водіння, і демпфування, можна знайти надзвичайно вузькі атрактори.
Вправа: Бейкер і Голлуб, Хаотична динаміка, сторінка 52, дають послідовність розділів Пуанкаре з0.2π інтервалами дляγ=1.5 і2β=0.75. Ви можете перевірити їх (і проміжні) за допомогою аплету, і спробувати уявити, щоб покласти їх у стек, щоб візуалізувати повний тривимірний атрактор!
