1.4: Принцип невизначеності
- Page ID
- 76801
Хвилі нечіткі
Як ми показали для хвильових пакетів, хвильова природа частинок передбачає, що ми не можемо знати як положення, так і імпульс частинки з довільним ступенем точності - якщо\(\Delta x\) представляє невизначеність у наших знаннях про положення та\(\Delta p\) імпульс, потім
\[ \Delta p \Delta x \sim h \tag{1.4.1} \]
де\(h\) константа Планка. У реальному світі частинки тривимірні, і ми повинні сказати\[ \Delta p_x \Delta x \sim h \tag{1.4.2} \]
з відповідними рівняннями для двох інших просторових напрямків. Нечіткість щодо позиції пов'язана з імпульсом в тому ж напрямку.
Давайте подивимося, як це працює, намагаючись дуже точно виміряти y -позицію та y -імпульс. Припустимо, у нас є джерело електронів, скажімо, електронна гармата в ЕПТ (електронно-променева трубка, наприклад старомодний монітор). Балка трохи розтікається, але якщо ми вставимо лист металу з щілиною ширини\(w\), то для частинок, які роблять його через щілину, ми знаємо\(y\) з невизначеністю\(\Delta y=w\). Тепер, якщо щілина знаходиться довгий шлях нижче за течією від джерела електронної гармати, ми також\(p_y\) дуже точно знаємо, як електрон досягає щілини, тому що для того, щоб дістатися до щілини, швидкість електрона повинна бути спрямована правильно.
Але чи впливає вимірювання y положення електрона - іншими словами, якщо він проходить через щілину - впливає на його імпульс у? Відповідь - так. Якщо це не так, то відправляючи потік частинок через щілину, вони всі потрапили б дуже близько до тієї ж точки на екрані, розміщеному далі за течією. Але ми знаємо з експерименту, що це не те, що відбувається - формується одна щілинна дифракційна картина кутової ширини\(\theta \sim \lambda/w\), де довжина хвилі електрона де\(\lambda\) Брольє задається\(p_x \cong h/\lambda\) (є незначний внесок\(\lambda\) від y -імпульсу). Послідовна невизначеність\(p_y\) в
\[ \Delta p_y/p_x \sim \theta \sim \lambda/w \tag{1.4.3} \]
Вставляючи\(p_x = h/\lambda\), ми відразу виявляємо, що
\[ \Delta p_y \sim h/w \tag{1.4.4} \]
Таким чином, акт вимірювання y положення електрона розмив його y імпульс саме на величину, необхідну за принципом невизначеності.
Намагаючись перемогти принцип невизначеності
Для того, щоб краще зрозуміти принцип невизначеності, давайте спробуємо побачити, що йде не так, коли ми насправді намагаємося виміряти позицію та імпульс точніше, ніж дозволено.
Наприклад, припустимо, ми дивимося на електрон через мікроскоп. Що ми могли очікувати побачити? Звичайно, ви знаєте, що якщо ми спробуємо подивитися на щось дуже маленьке через мікроскоп, воно стає розмитим - маленький гострий предмет отримує дифракційні візерунки по краях, що вказує на те, що ми дивимося на щось розміром, порівнянне з довжиною хвилі використовуваного світла. Якщо ми подивимось на щось набагато менше, ніж довжина хвилі світла - як електрон - ми очікуємо дифракційної картини концентричних кілець з круговою крапкою посередині. Розмір малюнка в порядку дорівнює довжині хвилі світла, адже з оптики це може бути показано,\(\sim\lambda f/d\) де\(d\) діаметр об'єктивної лінзи мікроскопа,\(f\) фокусна відстань (відстань від лінзи до об'єкта). Візьмемо\(f /d \sim 1\), як це зазвичай є. Отже, дивлячись на об'єкт розміром з електрон, повинен дати дифракційну картину, зосереджену на місці розташування об'єкта. Це, здавалося б, досить точно закріплює свою позицію.
А як щодо імпульсу електрона? Тут виникає проблема, яка не має значення для великих об'єктів - світло, яке ми бачимо, звичайно, відскочив від електрона, і тому електрон має певний імпульс віддачі. Тобто, відскакуючи світло від електрона, ми надали йому певний імпульс. Чи можемо ми сказати, скільки? Щоб зробити це простим, припустимо, у нас хороші очі і потрібно лише відскочити один фотон від електрона, щоб побачити його. Ми знаємо початковий імпульс фотона (тому що ми знаємо напрямок світлового променя, який ми використовуємо для освітлення електрона), і ми знаємо, що після відскоку фотон потрапляє в об'єктив об'єкта і проходить через мікроскоп, але ми не знаємо, де фотон потрапив на об'єктивну лінзу. Вся суть мікроскопа полягає в тому, що все світло з точки, світло, яке потрапляє на об'єктив об'єкта в різних місцях, все фокусується назад в одній точці, утворюючи зображення (крім розмиттості, згаданої вище). Отже, якщо світло має довжину хвилі\(\lambda\), його складові фотони мають імпульс\(\sim h/\lambda\), і від нашого незнання того, де фотон увійшов в мікроскоп, ми не впевнені в його x -напрямку імпульсу на величину\(\sim h/\lambda\). Обов'язково, тоді ми маємо таку ж невизначеність щодо імпульсу x -напрямку електрона, оскільки це було надано фотоном, що відскакує.
Але зараз у нас проблема. У наших спробах мінімізувати невизначеність імпульсу електрона, використовуючи лише один фотон для його виявлення, ми не побачимо значної частини дифракційної картини, розглянутої вище - такі дифракційні моделі генеруються багатьма фотонами, що потрапляють на плівку, сітківку або будь-яке обладнання для виявлення. використовується. Один фотон генерує одну точку (в кращому випадку!). Ця точка, швидше за все, буде знаходитися в порядку\(\lambda\) від центру візерунка, але це залишає нас з невизначеністю в позиції порядку \(\lambda\).
Тому, намагаючись спостерігати положення і імпульс одного електрона за допомогою одного фотона, ми знаходимо невизначеність як в положенні\(\Delta x\sim\lambda\), так і в імпульсі\(\Delta p_x\sim h/\lambda\). Ці результати відповідають принципу невизначеності Гейзенберга\(\Delta x\Delta p_x\sim h\).
Звичайно, ми могли б закріпити позицію набагато краще, якби ми використовували\(N\) фотони замість одного. З статистичної теорії відомо, що залишилася невизначеність\(\sim \lambda/\sqrt{N}\). Але тоді\(N\) фотони відскочили від електрона, тому, оскільки кожен з них однаково ймовірно пройшов через будь-яку частину об'єктивної лінзи, невпевненість в імпульсі електрона внаслідок цих зіткнень зростає як\(\sqrt{N}\). (Те саме, що середній дисбаланс між головами і хвостами в послідовності сальто\(N\) монет.)
Відзначаючи, що невизначеність в імпульсі електрона виникає тому, що ми не знаємо, де відскочений фотон проходить через об'єктивну лінзу, спокусливо думати, що ми могли б просто використовувати меншу об'єктивну лінзу, яка б зменшилася\(\Delta p_x\). Хоча це правильно, нагадаємо зверху, що ми заявляли розмір дифракційної картини був\(\sim \lambda f/d\), де\(d\) діаметр об'єктивної лінзи і\(f\) її фокусна відстань. Легко помітити, що дифракційна картина, а отже\(\Delta x\), стає більшою лише на суму, яка\(\Delta p_x\) стає меншою!
Спостереження за електронами в експерименті з подвійною щілиною
Припустимо, тепер, коли в експерименті з подвійною щілиною ми поставили собі за мету визначити, через яку щілину проходить кожен електрон, сяючи світло безпосередньо за екраном і спостерігаючи за відбитим світлом від електрона відразу після того, як він пройшов через щілину. Після обговорення в лекціях Фейнмана з фізики, том III, ми тепер встановимо, що якщо ми зможемо виявити електрони, ми зруйнуємо дифракційну картину!
Беручи відстань між двома прорізами\(d\), темні лінії в дифракційному малюнку знаходяться під кутом\[ (n+\frac{1}{2})\lambda_{elec}=d\sin\theta \tag{1.4.5} \]
Якщо світло, яке використовується для того, щоб побачити, через яку щілину проходить електрон, породжує невизначеність у\(\Delta p_y\)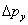 
імпульсі електрона y, щоб не зруйнувати дифракційну картину, ми повинні мати\[ \Delta p_y/p <\lambda_{elec}/d \tag{1.4.6} \]
(кутова невизначеність у напрямку електрона не повинна бути достатньою для поширення його від максимумів дифракційної картини в мінімуми). \(p\)Ось повний імпульс електрона,\(p=h/\lambda_{elec}\). Тепер невизначеність у імпульсі електрона y, шукаючи його за допомогою мікроскопа, є\(\Delta p_y \sim h/\lambda_{light}\).
Підставляючи ці значення в нерівність вище, ми знаходимо умову для виживання дифракційної картини є\[ \lambda_{light}>d \tag{1.4.7} \]
довжина хвилі світла, використовуваного для виявлення якої щілини пройшов електрон, повинна бути більше, ніж відстань між щілинами. На жаль, світло, розсіяне від електрона, дає одну точку в дифракційній схемі розміру довжини хвилі використовуваного світла, тому навіть якщо ми бачимо спалах, це не пригнічує електрон достатньо, щоб сказати, через яку щілину він пройшов. Гейзенберг знову перемагає.
Як принцип невизначеності визначає розмір всього
Цікаво подивитися, як фактичний фізичний розмір атома водню визначається хвильовою природою електрона, по суті, принципом невизначеності. У наземному стані атома водню електрон мінімізує його загальну енергію. Для класичного атома енергія буде мінус нескінченність, припускаючи, що ядро є точкою (і дуже великою в будь-якому випадку), оскільки електрон буде сидіти прямо на вершині ядра. Однак цього не може статися в квантовій механіці. Такий дуже локалізований електрон мав би дуже велику невизначеність в моменті - іншими словами, кінетична енергія була б великою. Це найбільш чітко видно, уявляючи, що електрон йде по круговій орбіті радіуса \(r\)з кутовим імпульсом\(h/2p\). Тоді одна довжина хвилі електрона de Broglie просто підходить навколо кола,\(\lambda_{elec}=2\pi r\). Зрозуміло, що коли ми зменшуємо радіус кола\(r\), пропорційно\(\lambda_{elec}\) знижується, і електрони імпульсу
\[ p=h/\lambda_{elec}=h/2\pi r \tag{1.4.8} \]
збільшується. Додавши електростатичну потенційну енергію електрона, ми знаходимо загальну енергію для кругової орбіти радіуса\(r\):
\[ E(r)=K.E.+P.E.=\frac{p^2}{2m}-\frac{e^2}{4\pi \varepsilon_0r}=\frac{h^2}{8m\pi^2r^2}-\frac{e^2}{4\pi\varepsilon_0r} \tag{1.4.9} \]
Зверніть увагу\(r\), що для дуже великих потенційна енергія домінує, кінетична енергія незначна, а скорочення атома знижує загальну енергію. Однак для досить\(r\) малих (завжди позитивний) термін кінетичної енергії виграє, і загальна енергія зростає в міру скорочення атома. Очевидно, тоді має бути значення,\(r\) для якого загальна енергія мінімальна. Візуалізація графіка загальної енергії, заданої рівнянням вище як функція\(r\), в мінімальній точці нахил\(E(r)\) дорівнює нулю,\(dE(r)/dr=0\).
Тобто,
\[ -\frac{h^2}{4m\pi^2r}+\frac{e^2}{4\pi \varepsilon_0}=0 \tag{1.4.10} \]
подача
\[ r_{min}=\frac{\varepsilon_0h^2}{\pi me^2} \tag{1.4.11} \]
Загальна енергія для цього радіуса є точною правильною відповіддю, яка заспокоює (але ми цього не заслуговуємо, тому що ми використали наївну картину, як стане зрозуміло пізніше).
Сенс цієї вправи полягає в тому, щоб побачити, що в квантовій механіці, на відміну від класичної механіки, частинка не може позиціонувати себе на точному мінімумі потенційної енергії, оскільки це вимагатиме дуже вузького хвильового пакета і, таким чином, буде дорогим в кінетичній енергії. Основний стан квантової частинки в привабливому потенціалі є компромісом між мінімізацією потенційної енергії та мінімізацією кінетичної енергії. Таким чином, фізичні розміри атомів, молекул і в кінцевому підсумку нас визначаються константою Планка.