Skip to main content
LibreTexts - Ukrayinska

7.E: Координати (вправи)

  1. Last updated
  2. Save as PDF
  • Page ID
    77225

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Q1

    У прикладі 7.4.2 обговорюються полярні координати в евклідовій площині. Використовуйте техніку, продемонстровану в розділі 7.3, щоб знайти метрику в цих координатах.

    Q2

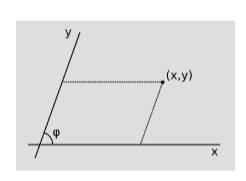
    Рис. 7.e.q2.png

    Похилі декартові координати схожі на звичайні декартові координати в площині, але їх осі знаходяться під кутом одна\(\varphi \neq \pi /2\) до одної. Показати, що метрика в цих координатах є

    \[ds^2 = dx^2 + dy^2 + 2cos\varphi dxdy\]

    Q3

    Нехай рівнянням\(U\) буде визначено\(3\) -площину в координатах Мінковського\(x = t\). Це площина простір, схожий на час, або світло? Знайдіть ковектор\(S\to \), який є нормальним до\(U\) в сенсі, описаному в розділі 7.6, описуючи його з точки зору його складових. Обчислити вектор\(S\), також у вигляді компонента. Переконайтеся, що\(S\to S = 0\). Показати,\(\to S\) що дотичне до\(M\).

    Q4

    Для косих декартових координат, визначених у задачі Q2, використовуйте детермінант метрики, щоб показати, що тензор Леві-Чивіта дорівнює

    \[\epsilon = \begin{pmatrix} 0 & \sin \varphi \\ -\sin \varphi & 0 \end{pmatrix}\]

    Q5

    Використовуйте методику, продемонстровану в прикладі 7.6.6, щоб знайти об'єм одиничної сфери.